《数据结构》C语言版——递归遍历二叉树
和小萌新一起读注释,敲代码,把代码跑起来!
//头文件Bin Tree.h
#pragma once
//同一个文件不会被包含多次。注意这里所说的“同一个文件”是指物理上的一个文件,而不是指内容相同的两个文件。
#include//源文件Bin Tree.cpp
#include"Bin Tree.h"
/*初始化二叉树*/
void InitBinTree(BinTree *bt,ElemType ref)
{
bt->root=NULL;
bt->refvalue=ref;//空标记
}
/*创建二叉树——以地址传递方式创建*/
void createBinTree_1(BinTree *bt)//对外进行调用
{
createBinTree_1(bt,&(bt->root));
}
void createBinTree_1(BinTree *bt,BinTreeNode **t)//承载函数(方法)
//BinTreeNode **t,因为根节点root已经是一个指针,当修改根节点时,所以用二级指针传递地址
{
ElemType Item;
scanf("%c",&Item);//输入数据
if(Item==bt->refvalue)//如果输入的数据正好是空标记
(*t)=NULL;//则根节点为空
else
{
//真实创建节点
(*t)=(BinTreeNode*)malloc(sizeof(BinTreeNode));//创建结点
assert(*t!=NULL);//判断结点是否创建成功
(*t)->data=Item;//根节点创建完成
//递归调用
createBinTree_1(bt,&((*t)->leftChild));//创建根节点后,创建根的左子树,并用地址传递
createBinTree_1(bt,&((*t)->rightChild));//创建根节点后,创建根的右子树,并用地址传递
}
}
/*创建二叉树——引用*/
void createBinTree_2(BinTree *bt)
{
createBinTree_2(bt,bt->root);
}
void createBinTree_2(BinTree *bt,BinTreeNode *&t)
{
ElemType Item;
scanf("%c",&Item);//输入数据
if(Item==bt->refvalue)//如果输入的数据正好是空标记
t=NULL;//则根节点为空
else
{
t=(BinTreeNode*)malloc(sizeof(BinTreeNode));//创建结点
assert(t!=NULL);
t->data=Item;//根节点创建完成
createBinTree_2(bt,t->leftChild);//递归创建根的左子树
createBinTree_2(bt,t->rightChild);//递归创建根的右子树
}
}
/*创建二叉树——读入字符串创建*/
void createBinTree_3(BinTree *bt,char *str)
{
createBinTree_3(bt,bt->root,str);
}
void createBinTree_3(BinTree *bt,BinTreeNode *&t,char *&str)//引用传递
{
if(*str==bt->refvalue)
t=NULL;
else
{
t=(BinTreeNode*)malloc(sizeof(BinTreeNode));
assert(t!=NULL);
t->data=*str;
createBinTree_3(bt,t->leftChild,++str);
createBinTree_3(bt,t->rightChild,++str);
}
}
/*前序遍历*/
void PreOrder(BinTree *bt)
{
PreOrder(bt->root);
}
void PreOrder(BinTreeNode *t)
{
if(t!=NULL)
{
printf("%c ",t->data);//先访问根
PreOrder(t->leftChild);//访问左子树
PreOrder(t->rightChild);//访问右子树
}
}
/*中序遍历*/
void InOrder(BinTree *bt)
{
InOrder(bt->root);
}
void InOrder(BinTreeNode *t)
{
if(t!=NULL)//如果树根不为空
{
InOrder(t->leftChild);//先访问左子树(之前根的左子树成为现在的根,继续判断根是否为空,若不为空,继续访问下一个左子树;若为空,则依次返回左子树)
printf("%c ",t->data);//访问根
InOrder(t->rightChild);//访问右子树
}
}
/*后序遍历*/
void PostOrder(BinTree *bt)
{
PostOrder(bt->root);
}
void PostOrder(BinTreeNode *t)
{
if(t!=NULL)
{
PostOrder(t->leftChild);//访问左子树
PostOrder(t->rightChild);//访问右子树
printf("%c ",t->data);//访问根
}
}
/*求二叉树的节点个数*/
int Size(BinTree *bt)
{
return Size(bt->root);
}
int Size(BinTreeNode *t)
{
if(t==NULL)
return 0;//空树节点个数为0
else
return Size(t->leftChild)+Size(t->rightChild)+1;//1为根节点
}
/*求二叉树的高度*/
int Height(BinTree *bt)
{
return Height(bt->root);
}
int Height(BinTreeNode *t)
{
if(t==NULL)
return 0;
else
{
int left_height=Height(t->leftChild);
int right_height=Height(t->rightChild);
return (left_height>right_height ? left_height:right_height)+1;
}
}
/*查找二叉树的节点*/
BinTreeNode* Search(BinTree *bt,ElemType key)
{
return Search(bt->root,key);
}
BinTreeNode* Search(BinTreeNode *t,ElemType key)
{
if(t==NULL)
return NULL;
if(t->data=key)
return t;
BinTreeNode *p=Search(t->leftChild,key);
if(p!=NULL)//如果p为空,则继续查找右子树,否则在左子树中已经找到
return p;
return Search(t->rightChild,key);
}
/*查找二叉树的节点的父节点*/
BinTreeNode* Parent(BinTree *bt,BinTreeNode *p)
{
return Parent(bt->root,p);
}
BinTreeNode* Parent(BinTreeNode *t,BinTreeNode *p)
{
if(t==NULL || p==NULL)
return NULL;
if(t->leftChild==p || t->rightChild==p)
//t一定是p的父节点
return t;
//如果t的左右子树不是p
BinTreeNode *q=Parent(t->leftChild,p);//在t的左子树查找p节点
if(q!=NULL)//如果q不为空说明在左子树中找到
return q;//返回父节点
return Parent(t->rightChild,p);//否则直接返回右子树父节点的查找
}
/*求某个节点的左子树*/
BinTreeNode* LeftChild(BinTreeNode *p)
{
if(p!=NULL)
return p->leftChild;
return NULL;
}
/*求某个节点的右子树*/
BinTreeNode* RightChild(BinTreeNode *p)
{
if(p!=NULL)
return p->rightChild;
return NULL;
}
/*二叉树是否为空*/
bool BinTreeEmpty(BinTree *bt)
{
return bt->root==NULL;//空等于空返回真,不空返回假
}
/*拷贝二叉树*/
void Copy(BinTree *bt1,BinTree *bt2)
{
Copy(bt1->root,bt2->root);
}
void Copy(BinTreeNode *&t1,BinTreeNode *t2)
{
if(t2==NULL)
t1=NULL;
else
{
t1=(BinTreeNode*)malloc(sizeof(BinTreeNode));
assert(t1!=NULL);
t1->data=t2->data;
Copy(t1->leftChild,t2->leftChild);
Copy(t1->rightChild,t2->rightChild);
}
}
/*清除二叉树*/
void BinTreeClear(BinTree *bt)
//每释放一个节点的前提是先释放其左子树和其右子树
{
BinTreeClear(bt->root);//给出根节点
}
void BinTreeClear(BinTreeNode *&t)//更改给出引用
{
if(t!=NULL)
{
BinTreeClear(t->leftChild);
BinTreeClear(t->rightChild);
free(t);
t=NULL;
}
}
//源文件Main.cpp
#include"Bin Tree.h"
void main()
{
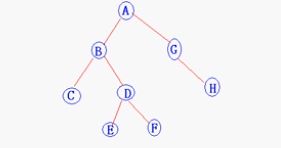
char *str="ABC##DE##F##G#H##";
BinTree mytree;
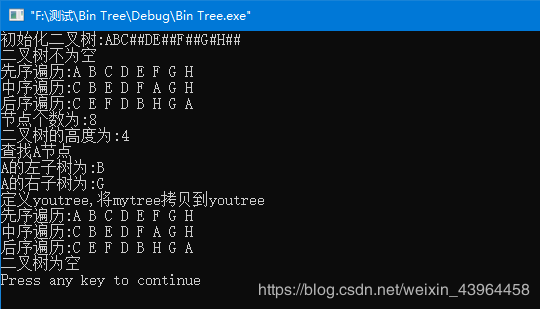
printf("初始化二叉树:ABC##DE##F##G#H##");
printf("\n");
InitBinTree(&mytree,'#');//'#'为结束标记
BinTree youtree;
InitBinTree(&youtree,'#');
// createBinTree_1(&mytree);
// createBinTree_2(&mytree);
createBinTree_3(&mytree,str);
if(!BinTreeEmpty(&mytree))
printf("二叉树不为空");
printf("\n");
printf("先序遍历:");
PreOrder(&mytree);
printf("\n");
printf("中序遍历:");
InOrder(&mytree);
printf("\n");
printf("后序遍历:");
PostOrder(&mytree);
printf("\n");
printf("节点个数为:%d\n",Size(&mytree));
printf("二叉树的高度为:%d\n",Height(&mytree));
printf("查找A节点");
printf("\n");
BinTreeNode *p=Search(&mytree,'A');//指针p指向B节点
BinTreeNode *parent=Parent(&mytree,p);
BinTreeNode *lp=LeftChild(p);
printf("A的左子树为:%c\n",lp->data);
BinTreeNode *rp=RightChild(p);
printf("A的右子树为:%c\n",rp->data);
printf("定义youtree,将mytree拷贝到youtree");
printf("\n");
Copy(&youtree,&mytree);//mytree拷贝youtree
printf("先序遍历:");
PreOrder(&youtree);
printf("\n");
printf("中序遍历:");
InOrder(&youtree);
printf("\n");
printf("后序遍历:");
PostOrder(&youtree);
printf("\n");
BinTreeClear(&youtree);
BinTreeClear(&mytree);
if(BinTreeEmpty(&mytree))
printf("二叉树为空");
printf("\n");
}