求连通分量（DFS）（BFS）（STL）

求连通分量

Description
求一个图的连通分量

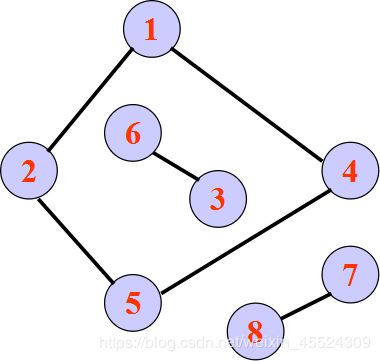
Input
n 顶点数小于等于100
Output
连通分量
Sample Input
8
6 3
1 2
2 5
5 4
4 1
8 7
0 0

AC代码

1.深搜（邻接矩阵）

建立一个矩阵，然后暴力搜下去，容易理解

#include
using namespace std;
int b[105],a[105][105],x,y,n,o,sum;
void dfs(int i)
{
	b[i]=1;//出现过
	o++;//找连通分量
	for (int j=1;j<=n;j++)//一个一个点找
	if(a[i][j]&&!b[j])dfs(j);//搜下去
}
int main()
{
	cin>>n;
	while(cin>>x&&cin>>y)//输入
	{
		if(x+y==0)break;
		a[x][y]=1;a[y][x]=1;//无向图，两个都要
	}
	for(int i=1;i<=n;i++)
	{
	 if(b[i]==0){o=0;dfs(i);}//找没有被找到过的
	 sum=max(sum,o);//找最大	   
	}
	cout<<sum;
}

2.深搜（邻接表）

建立一个邻接表，比暴搜快，有点难理解

#include
using namespace std;
int b[105],head[10005],x,y,n,o,sum,tot;
struct stu//结构体
{
	int to,next;
}a[10005];//
void add(int x,int y)//邻接表建立
{
	tot++;
	a[tot].to=y;//连接自己的人
	a[tot].next=head[x];//下一个人
	head[x]=tot;//方便下一个人找到自己
}
void dfs(int i)
{
	b[i]=1;//避免重复
	o++;//找这个图的连通分量
	for(int j=head[i];j;j=a[j].next)//翻译为"j=head[i];while(j!=0){执行语句;j=a[j].next;}"就是从头找下去 
	if(!b[a[j].to])dfs(a[j].to);//往下搜
}
int main()
{
	cin>>n;
	while(cin>>x&&cin>>y)//输入
	{
		if(x+y==0)break;
        add(x,y);add(y,x);//无向图，两个都要
	}
	for(int i=1;i<=n;i++)
	{
	 if(b[i]==0){o=0;dfs(i);}//如果这个点没有被搜过，就搜
	 sum=max(sum,o);//找最大	   
	}
	cout<<sum;
}

3.广搜（邻接矩阵）

用广搜的方式去搜索这个矩阵，暴力，容易理解

#include
using namespace std;
int b[105],a[105][105],st[10005],x,y,n,o,sum,s,head,tail;
void bfs(int i)
{
	int head=0,tail=1;
	st[1]=i,b[i]=1;
	do{
		head++;
		for(int j=1;j<=n;j++)
		if(a[st[head]][j]&&!b[j])//判断有没有出现过
		{
			o++;//连通分量
			tail++;//尾巴加1
			b[j]=1;//出现过
			st[tail]=j;//存当前节点
		}
	}while(head<tail);
}
int main()
{
	cin>>n;
	while(cin>>x&&cin>>y)//输入
	{
		if(x+y==0)break;
		a[x][y]=1;a[y][x]=1;//双向图
	}
	for(int i=1;i<=n;i++)
	{
	 if(b[i]==0){o=0;bfs(i);} //搜没有搜过的点
	 sum=max(sum,o);	   //找最大
	}
	cout<<sum+1;//本身
}

4.广搜（邻接表）

用广搜去搜索已经建好的邻接表，快但难理解

#include
using namespace std;
int b[105],head[10005],st[10005],x,y,n,o,sum,tot;
struct stu//结构体
{
	int to,next;
}a[10005];
void add(int x,int y)//邻接表建立
{
	tot++;
	a[tot].to=y;//连接自己的
	a[tot].next=head[x];//下一个人
	head[x]=tot;//方便下一个人找自己
}
void bfs(int i)
{
	int h=0,tail=1;
	st[1]=i,b[i]=1;//找到了
	do{
		h++;
		for(int j=head[st[h]];j;j=a[j].next)//翻译为"j=head[sth[h]];while(j!=0){执行语句;j=a[j].next;}"就是从头找下去 
		if(!b[a[j].to])//有没有搜过
		{
		o++;//连通分量
		b[a[j].to]=1;//搜过
	    tail++;
		st[tail]=a[j].to;//搜下去
		}
	}while(h<tail);

}
int main()
{
	cin>>n;
	while(cin>>x&&cin>>y)//输入
	{
		if(x+y==0)break;
        add(x,y);add(y,x);//双向图
	}
	for(int i=1;i<=n;i++)
	{
	 if(b[i]==0){o=0;bfs(i);} 
	 sum=max(sum,o);	   //找最大
	}
	cout<<sum+1;//本身
}

5.STL（邻接表）

用STL中的队列模板来做，和广搜（邻接表）的速度一样
这里扩展队列的知识

和广搜（邻接表）的思路一样，就不在代码上写分析了

#include
#include
using namespace std;
int b[105],head[10005],x,y,n,o,sum,tot;
struct stu
{
	int to,next;
}a[10005];
void add(int x,int y)
{
	tot++;
	a[tot].to=y;
	a[tot].next=head[x];
	head[x]=tot;
}
void bfs(int i)
{
	int h=0,tail=1;
	queue<int>st;
	st.push(i);
	b[i]=1;
	while(st.size())
	{
	 int x=st.front(); 
	 st.pop();
	 for(int j=head[x];j;j=a[j].next)
		if(!b[a[j].to])
		{
			b[a[j].to]=1; 
			o++;
			st.push(a[j].to);
		}
	}
}
int main()
{
	cin>>n;
	while(cin>>x&&cin>>y)
	{
		if(x+y==0)break;
        add(x,y);add(y,x);
	}
	for(int i=1;i<=n;i++)
	{
	 if(b[i]==0){o=0;bfs(i);} 
	 sum=max(sum,o);	   
	}
	cout<<sum+1;
}

谢谢欣赏