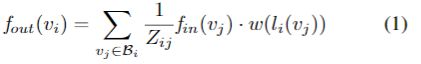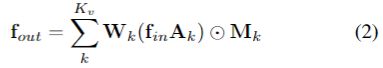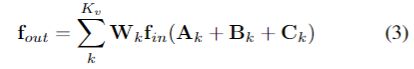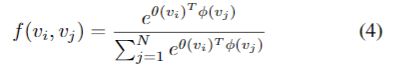翻译：Two-Stream Adaptive Graph Convolutional Networks for Skeleton-Based Action Recognition

Two-Stream Adaptive Graph Convolutional Networks for Skeleton-Based Action Recognition

双流自适应图卷积网络用于基于骨架的动作识别

论文地址：https://arxiv.org/abs/1805.07694

源码：https://github.com/lshiwjx/2s-AGCN

作者：Lei Shi，Yifan Zhang，Jian Cheng，Hanqing Lu

本文为CVPR2019 录用论文，由1National Laboratory of Pattern Recognition, Institute of Automation, Chinese Academy of Sciences2University of Chinese Academy of Sciences3CAS Center for Excellence in Brain Science and Intelligence Technology提出一种新的双流自适应图卷积网络（2sAGCN），用于基于骨架的动作识别。

摘要

在基于骨架的动作识别中，将人体骨架建模为时空图的图形卷积网络（GCN）取得了显著的性能。然而，在现有的基于GCN的方法中，图的拓扑结构是手动设置的，并且它固定在所有层和输入样本上。对于行动识别任务中的分层GCN和不同样本，这可能不是最佳选择。此外，在现有的方法中，很少研究骨骼数据的二阶信息（骨骼的长度和方向），这对于动作识别来说自然更具信息性和识别性。在这项工作中，我们提出了一种新的双流自适应图卷积网络（2sAGCN），用于基于骨架的动作识别。该模型中的图拓扑结构可以由BP算法以端到端的方式统一学习，也可以单独学习。这种数据驱动的方法提高了模型的灵活性，为适应各种数据样本带来了更广泛的通用性。此外，提出了一个双流框架，同时对一阶和二阶信息进行建模，这对识别精度有显著的提高。对两个大型数据集NTU-RGBD和Kinetics-Skeleton进行了大量的实验，证明我们的模型的性能超过了最先进的水平，并且有很大的差距。

介绍

基于骨架数据的动作识别方法因其对动态环境的适应性强、背景复杂而受到广泛研究和重视。传统的基于深度学习的方法将骨骼手动构造为一系列关节坐标向量或伪图像，其被馈送到RNN或CNN以生成预测。 然而，将骨架数据表示为矢量序列或2D网格不能完全表达相关关节之间的依赖性。 骨架自然地构造为非欧几里德空间中的图形，其中关节作为顶点并且它们在人体中作为边缘的自然连接。 先前的方法不能利用骨架数据的图形结构，并且难以概括为具有任意形式的骨架。 最近，图形卷积网络（GCN）在图像与图形之间推广了卷积，已成功应用于许多应用。 对于基于骨架的动作识别任务，Yan等人。 首先应用GCN来模拟骨架数据。 他们基于人体关节的自然连接构建空间图，并在连续帧中的相应关节之间添加时间边。 提出了一种基于距离的采样函数来构造图卷积层，并以此为基本模块来构造最终的时空图卷积网络（ST-GCN）。

然而，ST-GCN中的图构造过程存在三个缺点：（1）ST-GCN中使用的骨架图是启发式的预先定义的，只代表人体的物理结构，因此不能保证它对动作识别任务是最优的。例如，双手之间的关系对于识别诸如“拍手”和“阅读”之类的类很重要。然而，ST-GCN很难捕捉到双手之间的依赖关系，因为它们在预定义的人体图。（2）GCN的结构是层次结构，不同的层次包含多级语义信息。然而，ST-GCN中应用的图的拓扑结构在所有层上都是固定的，缺乏对所有层中包含的多级语义信息进行建模的灵活性和能力；（3）一个固定的图结构可能不适合所有不同作用类型的样本。例如对于“擦脸”和“摸头”这些类，手和头之间的联系应该更紧密，但对于其他一些类，如“跳起来”和“坐下来”则不是这样。这一事实表明，图表结构应该是数据相关的，然而，ST-GCN不支持这一点。

为了解决上述问题，本文提出了一种新的自适应图卷积网络。它参数化两种类型的图，其结构与模型的卷积参数一起训练和更新。一种类型是全局图，它表示所有数据的通用模式。另一种类型是单独的图形，它表示每个数据的唯一模式。这两种类型的图都针对不同的层进行了单独的优化，可以更好地适应模型的层次结构。这种数据驱动的方法提高了模型的灵活性，为适应各种数据样本带来了更广泛的通用性。

ST-GCN中另一个值得注意的问题是，每个顶点的特征向量只包含关节的二维或三维坐标，可以将其视为骨架数据的一阶信息。然而，代表两关节间骨骼特征的二阶信息并没有被利用。通常情况下，骨骼的长度和方向对于动作识别来说自然更具信息性和非犯罪性。为了利用骨骼数据的二阶信息，将骨骼的长度和方向表示为从其源关节指向目标关节的向量。与一阶信息类似，将矢量输入自适应图卷积网络中，对动作标签进行预测。提出了一种融合一阶和二阶信息的双流框架，进一步提高了系统的性能。

为了验证所提出的模型的优越性，即双流自适应图卷积网络（2s-AGCN），在两个大规模数据集上进行了大量实验：NTU-RGBD [27]和Kinetics-Skeleton [12] ]。 我们的模型在两个数据集上都实现了最先进的性能。

我们工作的主要贡献在于三个方面：（1）提出了一种自适应图卷积网络，以端到端的方式自适应地学习不同GCN层和骨架样本的图形拓扑，这样可以更好地适应动作识别任务和GCN的层次结构。 （2）使用双流框架明确地制定骨架数据的二阶信息并与一阶信息组合，这为识别性能带来了显着的改进。（3）在基于骨架的动作识别的两个大型数据集中，所提出的2s-AGCN显著超过了现有技术。 该代码将被发布以用于将来的工作并促进沟通。

2 相关工作

2.1 基于骨架的工作识别

基于骨架的动作识别的传统方法通常设计手工制作的特征来模拟人体[31,8]。 然而，这些基于手工特征的方法的性能几乎不令人满意，因为它不能同时考虑所有因素。 随着深度学习的发展，数据驱动方法已成为主流方法，其中最广泛使用的模型是RNN和CNN。 基于RNN的方法将骨架数据模拟为一系列坐标向量，每个坐标向量代表人体关节[6,27,22,29,33,19,20,3]。 基于CNN的方法基于手动设计的变换规则将骨架数据建模为伪图像[21,14,13,23,18,17]。 基于CNN的方法通常比基于RNN的方法更受欢迎，因为CNN具有更好的可并行性并且比RNN更容易训练。

然而，RNN和CNN都不能完全代表骨架数据的结构，因为骨架数据自然地以图的形式嵌入，而不是以矢量序列或二维网格的形式嵌入。最近，Yan等人[32]提出一种时空图卷积网络（ST-GCN），将骨架数据直接建模为图结构。它消除了设计手工部件分配或遍历规则的需要，从而比以前的方法获得更好的性能。

2.2 图卷积神经网络

关于图卷积的研究已经很多，构造GCN的原理主要遵循两条流：空间透视和光谱透视[28，2，11，25，1，16，7，5，9，24，15]。空间透视法直接对图形顶点及其邻接点进行卷积滤波，提取和归一化是基于人工设计的规则[7，25，9，24，15]，与空间透视法相比，光谱透视法利用图拉普拉斯矩阵的特征值和特征向量。这些方法借助于图傅立叶变换[28]在频域中执行图卷积，在每个卷积步骤[2，11，16，5]中不需要从图中提取局部连接区域。这项工作遵循空间透视法。

3 图卷积网络

3.1 图结构

一帧中的原始骨架数据始终作为矢量序列提供。 每个矢量表示相应人体关节的2D或3D坐标。 完整操作包含多个不同长度的帧，用于不同的样本。 我们使用时空图来模拟这些关节沿空间和时间维度的结构化信息。 该图的结构遵循ST-GCN [32]的工作。 图1中的左侧草图呈现了构造的时空骨架图的示例，其中关节被表示为顶点，并且它们在人体中的自然连接被表示为空间边缘（图1中的橙色线，左边）。 对于时间维度，两个相邻帧之间的对应关节与时间边缘连接（图1中的蓝线，左边）。 将每个关节的坐标向量设置为对应顶点的属性。

图1.（a）ST-GCN中使用的时空图的示意图。 （b）映射策略的说明。 不同的颜色表示不同的子集。

3.2图卷积

给定上面定义的图形，在图形上应用多层时空图卷积运算以提取高级特征。 然后使用全局平均池化层和softmax分类器，根据提取的特征来预测动作类别。

在空间维度中，顶点vi上的图卷积运算公式为[32]:

其中f表示特征图，v表示图的顶点。bi表示vi卷积的采样区域，定义为目标顶点（vi）的1距离相邻顶点（vj）。w是与原始卷积操作类似的加权函数，它根据给定的输入提供权重向量。注意，卷积的权向量数是固定的，而bi中的顶点数是可变的。为了用一个唯一的权重向量映射每个顶点，在ST-GCN[32]中专门设计了一个映射函数li。图1中的右草图显示了这种策略，其中×表示骨架的重心。bi是曲线所包围的区域。具体来说，该策略根据经验将内核大小设置为3，并自然地将bi分为3个子集：si1是顶点本身（图1中的红色圆圈，右）；si2是向心子集，其中包含靠近重心的相邻顶点（绿色圆圈）；si3是离心子集，包含离重心较远的相邻顶点（蓝圈）。zij表示包含vj的sik的基数。它旨在平衡每个子集的贡献.

3.3 实现

在空间维度中实现图卷积并不简单。 具体地，网络的特征图实际上是C×T×N张量，其中N表示顶点数，T表示时间长度，C表示信道数。 为了实现ST-GCN，将等式1转化为

其中Kv表示空间维的核大小。利用上面设计的分区策略，Kv设置为3. ，其中 ̄Ak类似于N×N邻接矩阵，其元素 ̄Aijk表示 顶点vj是否在顶点vi的子集Sik中。 它用于从对应的权重向量的fin中提取特定子集中的连通顶点。Λ iik =Σj( ̄Aijk）+α是归一化对角矩阵.α设置为0.001以避免空行。 Wk是1×1卷积运算的Cout×Cin×1×1权重向量，其表示等式1中的加权函数w。Mk是N×N注意力图，表示每个顶点的重要性.⊗表示点积。

 

对于时间维度，由于每个顶点的邻域数固定为2（两个连续帧中的对应关节），因此可以直接执行与经典卷积操作类似的图卷积。具体地说，我们在上面计算的输出特征图上进行kt×1卷积，其中kt是时间维度的核大小。

4 双流自适应图卷积网络

在本节中，我们详细介绍了我们提出的双流自适应图卷积网络（2sAGCN）的组成部分。

4.1 自适应图卷积层

上面描述的骨架数据的时空图卷积是基于一个预定义的图计算的，这可能不是第1节中解释的最佳选择。为了解决这个问题，我们提出了一种自适应图卷积层。它使图的拓扑结构与网络的其他参数一起以端到端的学习方式进行优化。该图对于不同的层和样本是唯一的，这大大提高了模型的灵活性。同时，它被设计为一个残差分支，保证了原模型的稳定性，具体来说，根据式2，图的拓扑结构实际上是由邻接矩阵和掩模（即AK和MK）分别决定的。AK决定两个顶点之间是否有连接，MK决定连接的强度。为了使图形结构具有适应性，我们将等式2改为以下形式：

主要区别在于图的邻接矩阵，它分为三部分：Ak，Bk和Ck。

第一部分（Ak）与方程式中的原始归一化N×N邻接矩阵Ak相同。 它代表了人体的物理结构。

第二部分（Bk）也是N×N邻接矩阵。 与Ak相反，Bk的元素与训练过程中的其他参数一起参数化和优化。 Bk的值没有限制，这意味着根据训练数据完全学习图表。 通过这种数据驱动的方式，模型可以学习完全针对识别任务的图形，并且针对不同层中包含的不同信息更加个性化。 注意，矩阵中的元素可以是任意值。 它不仅表明两个关节之间存在连接，而且还表明连接的强度。 它可以起到与等式2中Mk执行的注意机制的相同作用。然而，原始注意矩阵Mk是点乘以Ak，这意味着如果Ak中的一个元素是0，它将始终为0，而​​不管 Mk的值。 因此，它无法生成原始物理图中不存在的新连接。 从这个角度来看，Bk比Mk更灵活。

第三部分（ck）是一个数据相关图，它为每个样本学习一个唯一的图。为了确定两个顶点之间是否存在连接以及连接的强度，我们使用归一化的嵌入高斯函数来计算两个顶点的相似性。

其中N是顶点的总数。 我们使用点积来度量嵌入空间中两个顶点的相似性。 详细地，给定尺寸为Cin×T×N的输入特征映射fin，我们首先将其嵌入具有两个嵌入函数的Ce×T×N，即θ和φ。 在这里，通过大量实验，我们选择一个1×1卷积层作为嵌入函数。 将两个嵌入的特征图重新排列并重新整形为N×CeT矩阵和CeT×N矩阵。 然后将它们相乘以获得N×N相似度矩阵Ck，其元素Cijk表示顶点vi和顶点vj的相似度。 矩阵的值归一化为0-1，用作两个顶点的软边。 由于归一化高斯具有SoftMax操作，我们可以根据等式4计算Ck如下：

其中Wθ和Wφ分别是嵌入函数θ和φ的参数。

我们没有直接用BK或CK替换原始AK，而是将它们添加到其中。BK值和θ、φ参数初始化为0。这样可以在不降低原有性能的前提下增强模型的灵活性。

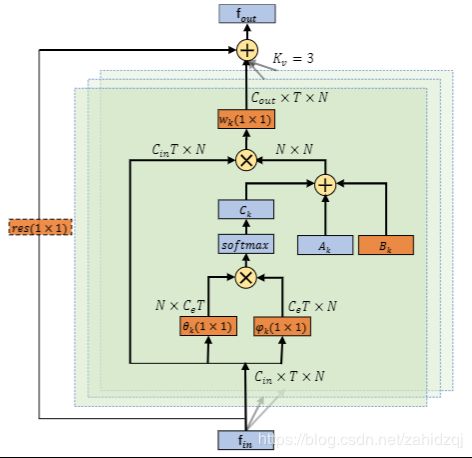
自适应图卷积层的总体结构如图2所示。除上面介绍的AK，Bk和Ck外，卷积的核大小（kv）与前面的设置相同，即3.wk是等式1中引入的加权函数，其参数为等式3中的wk。每个层都添加了一个类似于[10]的残差连接，这使得层可以插入到任何现有模型中，而不会破坏其初始行为。如果输入通道数与输出通道数不同，则在残差路径中插入1×1卷积（图2中带虚线的橙色框），以转换输入以匹配通道尺寸中的输出。

图2.自适应图卷积层的图示。每层中总共有三种类型的图，即Ak，Bk和Ck。 橙色框表示该参数是可学习的。（1×1）表示卷积的内核大小。 Kv表示子集的数量.⊕表示元素的总和.⊗表示matirx乘法。 只有当Cin与Cout不同时，才需要残留框（虚线）

4.2 自适应图卷积块

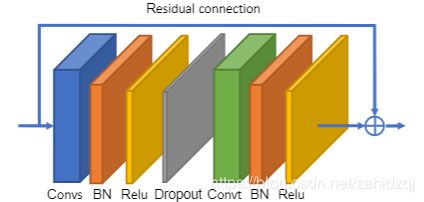
时间维度的卷积与ST-GCN相同，即在C×T×N特征图上执行KT×1卷积。空间GCN和时间GCN之后都有一个批标准化（BN）层和一个RELU层。如图3所示，一个基本块是一个空间GCN（convs）、一个时间GCN（convt）和一个附加的dropout层的组合，dropout率设置为0.5。为了稳定训练，为每个块添加一个残差连接

图3.自适应图卷积块的图示。 Convs表示空间GCN，Convt表示时间GCN，两者之后是BN层和ReLU层。 此外，为每个块添加残差连接。

4.3 自适应图卷积网络

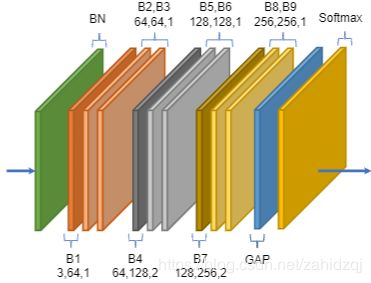
自适应图卷积网络（AGCN）是这些基本块的堆栈，如图4所示。 总共有9个块。 每个块的输出通道数为64,64,64,128,128,128,256,256和256.在开始时添加数据BN层以标准化输入数据。 执行全局平均池化层以将不同样本的特征映射池化为相同大小。 最终输出被发送到softmax分类器以获得预测。

图4.AGCN图示。共有9个区块（B1-B9）。每个块的三个数字分别代表输入通道数、输出通道数和步幅。GAP表示全局平均池化层

4.3 双流网络

正如第1节所介绍的，二阶信息，即骨骼信息，对于基于骨骼的动作识别也很重要，但在以前的工作中被忽略了。本文提出了一种二阶信息即骨骼信息的显式建模方法，该方法采用双流框架来增强识别能力。

特别是，由于每个骨骼都由两个关节绑定，因此我们定义靠近骨骼重心的关节是源关节，远离重心的关节是目标关节。每个骨骼都表示为从其源关节指向目标关节的向量，它不仅包含长度信息，还包含方向信息。例如，给定一个具有源关节v1=（x1，y1，z1）和目标关节v2=（x2，y2，z2）的骨骼，该骨骼的向量计算为ev1，v2=（x2−x1，y2−y1，z2−z1）。

由于骨骼数据的图形没有循环，因此可以为每个骨骼指定一个唯一的目标关节。关节的数量比骨骼的数量多一个，因为中心关节未指定给任何骨骼。为了简化网络的设计，我们在中心关节添加了一个值为0的空骨骼。这样，骨骼的图形和网络都可以设计成与关节相同的图形和网络，因为每个骨骼都可以绑定到一个唯一的关节，我们使用J-stream和B-stream分别表示关节和骨骼的网络。总体架构（2sAGCN）如图5所示。给定一个样本，我们首先根据关节的数据计算骨骼的数据。然后，关节数据和骨骼数据分别输入J流和B流。最后，将两个流的SoftMax分数相加，得到融合分数并预测动作标签。

图5.2sAGCN整体架构示意图。两个流的分数相加得到最终的预测。

5 实验

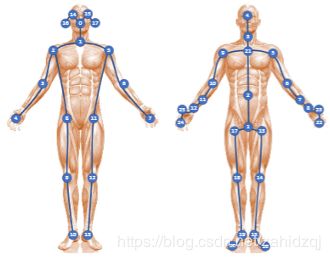
为了与ST-GCN进行直接比较，我们的实验是在相同的两个大规模动作识别数据集上进行的：NTU-RGBD [27]和Kinetics-Skeleton [12,32]。首先，由于NTU-RGBD数据集比Kinetics-Skeleton小，我们对其进行详尽的消融研究，以检验基于识别性能的所提出的模型组件的贡献。 然后，在两个数据集上评估最终模型以验证一般性，并与其他最先进的方法进行比较。 两个数据集中关节的定义及其自然连接如图6所示.

图6.左示意图显示Kinetics-Skeleton数据集的关节标签，右示意图显示NTU-RGBD数据集的关节标签。

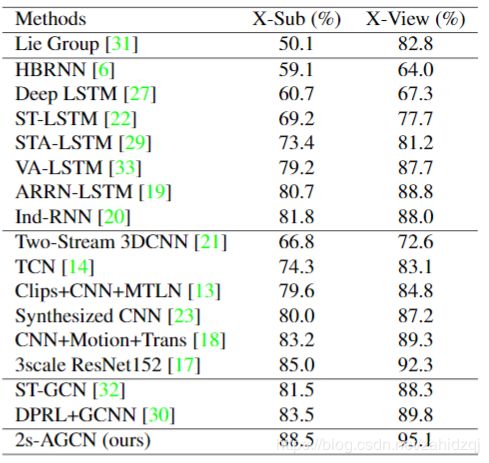
实验结果：与最先进的技术进行比较

表1.在NTU-RGBD数据集上与最新方法的验证准确性比较

表2.在Kinetics-Skeleton数据集上与最先进的方法进行验证准确性的比较