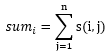[洛谷P2664]树上游戏-虚树-树上差分

树上游戏

题目描述

lrb有一棵树，树的每个节点有个颜色。给一个长度为n的颜色序列，定义s(i,j) 为i 到j 的颜色数量。以及

现在他想让你求出所有的sum[i]

输入输出格式

输入格式：

第一行为一个整数n，表示树节点的数量

第二行为n个整数，分别表示n个节点的颜色c[1],c[2]……c[n]

接下来n-1行，每行为两个整数x,y，表示x和y之间有一条边

输出格式：

输出n行，第i行为sum[i]

输入样例#1：

5
1 2 3 2 3
1 2
2 3
2 4
1 5

输出样例#1：

10
9
11
9
12

说明

sum[1]=s(1,1)+s(1,2)+s(1,3)+s(1,4)+s(1,5)=1+2+3+2+2=10
sum[2]=s(2,1)+s(2,2)+s(2,3)+s(2,4)+s(2,5)=2+1+2+1+3=9
sum[3]=s(3,1)+s(3,2)+s(3,3)+s(3,4)+s(3,5)=3+2+1+2+3=11
sum[4]=s(4,1)+s(4,2)+s(4,3)+s(4,4)+s(4,5)=2+1+2+1+3=9
sum[5]=s(5,1)+s(5,2)+s(5,3)+s(5,4)+s(5,5)=2+3+3+3+1=12

对于40%的数据，n<=2000
对于100%的数据，1<=n,c[i]<=10^5

---

很巧妙，同时也很难想，且特别麻烦的一道题……
当然是对于咱这种不看题解直接有想法就开始作死的人来说

---

思路:
第一反应是启发式合并…..
然而貌似不可做……
于是想到点分治……
然后发现不会统计答案（其实是觉得点分治很难写（事实证明咱错了））

于是考虑将每种颜色分开计算贡献。
可以发现，对于某一种颜色，这种颜色的点将整棵树分成了很多块。
对于每一块中的所有点，当前颜色对它们与外面的世界相连的所有边都有1的贡献。
而对于每一个本来就是这种颜色的点，它连出去的每一条边这种颜色都有贡献。

可以发现这可以用差分方便地统计答案。
然而对每一种颜色遍历一次整棵树来打标记，这样的复杂度是巨大的。

于是考虑建虚树优化每次遍历的节点数，就可以快速出解了!

注意为了方便打标记，和普通虚树不同的是，需要在虚树内添加每个当前颜色的节点的所有直接儿子。
每次对于一块的加减，可以在块的开始处（这个点一定是某个当前颜色的节点的某个直接儿子）打上等同于总点数减去块的大小的标记，再在块的所有结束节点处删去这个标记。

于是就可以AC了!
由于咱赌5毛钱出题人并没有想过这个算法，所以数据没有针对性。
于是暂时成为了速度第一~
（发博客时此题通过量：8）

#include

using namespace std;

inline int read()
{
    int x=0;char ch=getchar();
    while(ch<'0' || '9'while('0'<=ch && ch<='9')x=x*10+(ch^48),ch=getchar();
    return x;
}

typedef long long ll;
const int K=21;
const int N=1e5+9;
vector<int> g[N],col[N],p;
int n,to[N<<1],nxt[N<<1],beg[N],c[N],stk[N],tot;
int fa[N][K],siz[N],dep[N],id[N],ed[N],dfn,top;
ll sum[N];

inline void add(int u,int v)
{
    to[++tot]=v;
    nxt[tot]=beg[u];
    beg[u]=tot;
}

inline void dfs(int u)
{
    id[u]=++dfn;
    siz[u]=1;
    for(int i=beg[u];i;i=nxt[i])
        if(fa[u][0]!=to[i])
        {
            dep[to[i]]=dep[u]+1;
            fa[to[i]][0]=u;
            dfs(to[i]);
            siz[u]+=siz[to[i]];
        }
    ed[u]=dfn;
}

inline int lca(int a,int b)
{
    if(dep[a]>dep[b])swap(a,b);
    for(int i=K-1;i>=0;i--)
        if(dep[fa[b][i]]>=dep[a])
            b=fa[b][i];
    if(a==b)return a;
    for(int i=K-1;i>=0;i--)
        if(fa[a][i]!=fa[b][i])
            a=fa[a][i],b=fa[b][i];
    return fa[a][0];
}

inline bool cmp(int a,int b)
{
    return id[a]inline void dfs2(int u,int cc)
{
    int rectop,tots=0;
    for(int i=0;iif(c[u]==cc)
        {
            ll bcnt=siz[g[u][i]];
            for(int j=rectop+1;j<=top;j++)
                    bcnt-=siz[stk[j]];
            sum[g[u][i]]+=n-bcnt;
            tots+=n-bcnt;
            for(int j=rectop+1;j<=top;j++)
                sum[stk[j]]-=n-bcnt;
            top=rectop;
        }
    }

    if(c[u]==cc)
    {
        stk[++top]=u;
        sum[u]+=n;
        for(int i=beg[u];i;i=nxt[i])    
            if(to[i]!=fa[u][0])
                sum[to[i]]-=n;
    }
    else if(u==1)
    {
        int bcnt=siz[u];
        for(int i=1;i<=top;i++)
            bcnt-=siz[stk[i]];
        sum[u]+=n-bcnt;
        for(int i=1;i<=top;i++)
            sum[stk[i]]-=n-bcnt;
    }
}

inline void dfs3(int u)
{
    if(fa[u][0])
        sum[u]+=sum[fa[u][0]];
    for(int i=beg[u];i;i=nxt[i])
        if(to[i]!=fa[u][0])
            dfs3(to[i]);
}

int main()
{
    n=read();
    for(int i=1;i<=n;i++)
        col[c[i]=read()].push_back(i);
    for(int i=1,u,v;i1]=1;
    fa[1][0]=0;
    dfs(1);
    for(int i=1;ifor(int j=1;j<=n;j++)
            fa[j][i]=fa[fa[j][i-1]][i-1];

    for(int cc=1;ccif(col[cc].empty())continue;

        p.clear();
        sort(col[cc].begin(),col[cc].end(),cmp);
        for(int i=1,e=col[cc].size();i1],col[cc][i]));
            for(int j=beg[col[cc][i]];j;j=nxt[j])
                if(to[j]!=fa[col[cc][i]][0])
                    p.push_back(to[j]);
        }
        p.push_back(col[cc][0]);
        for(int j=beg[col[cc][0]];j;j=nxt[j])
            if(to[j]!=fa[col[cc][0]][0])
                p.push_back(to[j]);
        p.push_back(1);
        sort(p.begin(),p.end(),cmp);
        int size=unique(p.begin(),p.end())-p.begin();

        stk[top=1]=1;
        g[1].clear();
        for(int i=1;iwhile(top && id[p[i]]>ed[stk[top]])
                top--;
            g[stk[top]].push_back(p[i]);
            stk[++top]=p[i];
        }

        top=0;
        dfs2(1,cc);
    }

    dfs3(1);
    for(int i=1;i<=n;i++)
        printf("%lld\n",sum[i]);
    return 0;
}