Manacher算法 + 回文自动机学习笔记
Manacher算法
先来看这样一道题
最长回文子串
我们知道,这道题可以用后缀数组 O ( n l o g n ) O(nlogn) O(nlogn)的时间复杂度内求出
但是这题 1.1 ∗ 1 0 7 1.1 * 10 ^ 7 1.1∗107的范围明摆着是卡后缀数组的
虽说一般来说出题人不会这么丧心病狂,但是有时会需要统计例如以每一个字符为中心的最长回文串长度,这时使用后缀数组就会比较麻烦。幸运的是,还有一种非常简单的线性解法(甚至比后缀数组还好写)—— M a n a c h e r Manacher Manacher算法
Manacher算法的大体思想
其实很简单。
首先,我们将每两个字符间插入一个#。这样就能确保原串中的每个回文子串在新串中都对应着一个长度为奇数的回文子串。
在两侧插入两个未出现的字符防止溢出。
如果一个回文串长度 = len,定义它的回文半径 = ( l e n + 1 ) / 2 = (len + 1) / 2 =(len+1)/2
设 c n t i cnt_i cnti表示以 i i i为对称中心的最长回文子串的回文半径。
我们从左往右依次考虑,设当前考虑到第 i i i位
假设以 [ 1 , i − 1 ] [1, i - 1] [1,i−1]为对称中心的最长回文子串对称中心为 p o s pos pos, 最右边界为 m a x r maxr maxr。
显然有 c n t p o s + p o s = m a x r cnt_{pos} + pos = maxr cntpos+pos=maxr
当 m a x r < i maxr < i maxr<i时,我们直接从 i i i开始往两边暴力扩展并计算
否则,
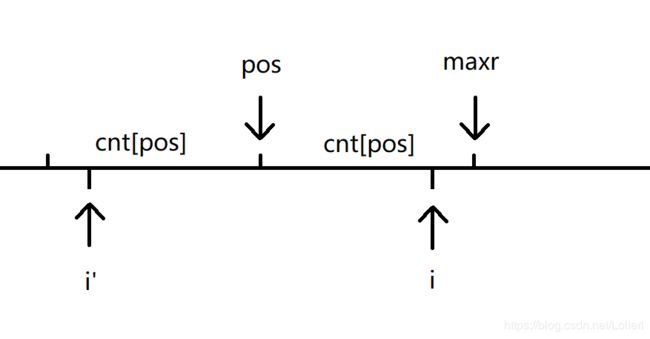
我们先考虑 i + c n t i < = m a x r i + cnt_i <= maxr i+cnti<=maxr的情况, 即当前回文子串右边界不超过 m a x r maxr maxr的情况
考虑 i i i关于 p o s pos pos的对称点 i ′ i' i′
我们发现,此时的每一个回文子串都恰好对应着一个以 i ′ i' i′为对称中心的相等的回文子串
什么意思?就是当当前回文子串的右边界不超过 m a x r maxr maxr时,我们将它的每个点都关于 p o s pos pos对称,由于小回文串的对称性,我们得到的是一个以 i ′ i' i′为对称中心的回文子串,且这两个回文子串由于大回文串的对称性而相等
而我们发现以 i ′ i' i′为中心的回文串我们先前已经计算过了
于是我们在 c n t i ′ 和 m a x r − i cnt_{i'}和maxr - i cnti′和maxr−i之间取个小(因为要确保 i + c n t i < = m a x r i + cnt_i <= maxr i+cnti<=maxr),然后继续暴力匹配即可
复杂度保证:
m a x r maxr maxr的长度单调不降且不会超过串长
由于每次匹配都会至少将 m a x r + 1 maxr + 1 maxr+1, 所以总复杂度是线性的
实现
代码:
#include回文自动机
M a n a c h e r Manacher Manacher算法虽然复杂度很优秀,但是功能有限仅限于统计长度。如果我们要统计一些其他的回文串相关的量,怎么实现呢?
比如这道题
第一眼:哇塞水题啊! m a n a c h e r manacher manacher + 差分就水过去了!
再仔细一看,发现它加了一个毒瘤的强制在线。
这里就要用到一种非常强大的数据结构——回文自动机。它是一种新颖的数据结构,2014年由一位俄罗斯信息学家提出。这里有一份原版记录
它可以回答以下询问:
- 询问每个前缀中本质不同回文子串个数
- 询问整个串中每个回文子串出现次数
- 一些其他问题
什么是回文自动机
回文自动机是一种有限状态自动机。
它和 m a n a c h e r manacher manacher算法没有太大的关系,思想更接近于AC自动机,如果已经熟练掌握AC自动机相关知识那么就会比较容易理解了。
回文自动机的结构是两颗树,我们先将它们叫做回文Trie树。其中的0号节点为长度为偶数的回文串的根,1号节点为长度为奇数的回文串的根。
它和trie一样,把信息存储在边上。不同点是它的每个节点(除了根)都表示一个回文串,一个节点向下连一条边 c h ch ch代表在它两边各加一个字符ch。只有1号节点例外,1号节点的孩子只增加一个字符,即为奇数长度回文串中心的字符。
容易证明任意回文串都可以在这两棵树上唯一地表示出来。
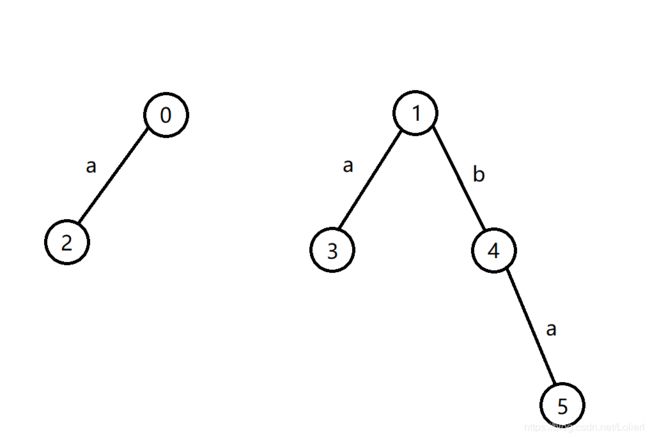
如图就是一棵回文trie树。它的每个节点所表示的回文串依次是(从2到5): a a , a , b , a b a aa, a, b, aba aa,a,b,aba
回文自动机的fail指针
和AC自动机类似,回文自动机被称为“自动机”是由于它的每个节点都有一个 f a i l fail fail指针,它指向当前节点所表示的回文串的最长回文后缀。
特殊地, 1 1 1号节点的 f a i l fail fail指针没有意义,原因一会会介绍到。 0 0 0号节点的 f a i l fail fail指针指向 1 1 1号节点。
回文自动机上还必须要记录每个节点所表示的最长回文串的长度,用 l e n len len表示。
上图中的 f a i l fail fail与 l e n len len的值如下表:
| i i i | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| f a i l i fail_i faili | 1 | 0 | 3 | 0 | 0 | 3 |
| l e n i len_i leni | 0 | -1 | 2 | 1 | 1 | 3 |
(此图只是为了帮助理解,真实构建时可能不会建出此形态的自动机)
注意我们定义 l e n 1 = − 1 len_1 = -1 len1=−1,原因是我们知道孩子的 l e n len len等于父亲的 l e n len len加 2 2 2,而我们将1的 l e n len len定义为 − 1 -1 −1这样它的孩子的 l e n len len就会直接被计算为 1 1 1,减少特判。还有一个好处一会会说到。
如何构建回文自动机
重点来了
之前已经介绍过,初始状态是有两个节点(0号和1号),它们的状态之前也已经说明。
我们从左往右加入字符串的每个字符
设 l a s t last last为上一次插入字符的节点编号,初始时 l a s t = 0 last = 0 last=0
对于每个字符我们需要在回文自动机上找到以它结尾的最长回文子串。
对于字符 i i i,
while(s[i - b[last].len - 1] != s[i])last = b[last].fail
这样求出的 l a s t last last即为新节点的父亲。
为什么呢?网上大多数dalao都说的很详细,还有高清大图。我比较懒我就大概讲讲自己的理解。
首先我们肯定要先考虑上一个位置在两边直接各加一个字符是否是回文串。
如果不是怎么办?那么我们就不停跳到它的最长回文后缀直到是回文为止。每次跳都能保证它是一开始 l a s t last last的一个回文后缀也就是指以 i − 1 i - 1 i−1结尾的回文子串,这样在它两边各加一个字符后,对应的一定是以当前字符为结尾的一个回文串。又由于每次都是跳最长的,所以第一次合法时取到的以 i i i结尾的回文子串也一定是最长的。
这个过程什么时候结束呢?由于 l e n 1 = − 1 len_1 = -1 len1=−1,所以在跳到1的时候必然是自己等于自己,必然可以回文。
然后我们就像 t r i e trie trie一样,在父亲下面生成孩子。
新孩子的 f a i l fail fail怎么计算呢?它就是从它父亲的 f a i l fail fail开始跳,跳到的第一个回文的位置。原因和上面类似,大家可以自己思考。
于是我们就愉快的建完了。
不同题目可能会需要在自动机上维护一些量。
比如
n u m i num_i numi:是 i i i节点表示的回文串后缀的本质不同回文串个数
维护方法: n u m i = n u m f a i l i + 1 num_i = num_{fail_i} + 1 numi=numfaili+1
s u m i sum_i sumi: i i i节点表示的回文串出现的次数
维护方法:每次 s u m i + + sum_i ++ sumi++,最后将 i i i的值累加到 f a i l i fail_i faili上
还有一些其他的量,大都不难通过 f a i l i fail_i faili和 i i i的父亲的值维护。
复杂度:
设 T = T = T= 字符集大小
则空间复杂度为 O ( n T ) , 时 间 复 杂 度 为 O ( n l o g T ) O(nT),时间复杂度为O(nlogT) O(nT),时间复杂度为O(nlogT)
(具体怎么证我也不知道qwq 背个结论吧)
如果空间需求太大可以使用指针也许也并没有什么用
实现:
【模板】回文自动机
模板题。注意由于要求以 i i i结尾,所以串长两两不等,这里的回文子串个数即为本质不同回文子串个数。
代码:
#include[APIO2014]回文串
经典的回文自动机题目。
做法:找出每个本质不同子串 维护 s u m sum sum 求 m a x max max即可
代码:
#include[SHOI2011]双倍回文
做法:题目中的条件经过分析之后等价于求最长的"长度为 4 4 4的倍数、且长度为它的长度的一半的后缀也为回文的回文子串"。所以在回文自动机上维护长度不超过 l e n / 2 len / 2 len/2的最长回文后缀为 t t t,然后统计所有长度为 4 4 4的倍数且 l e n t = = l e n i / 2 len_t == len_i / 2 lent==leni/2的回文串长度最大值即可。
代码:
#include