最小生成树的本质是什么？Prim算法道破天机

本文始发于个人公众号：TechFlow，原创不易，求个关注

今天是算法和数据结构专题20篇文章，我们继续最小生成树算法，来把它说完。

在上一篇文章当中，我们主要学习了最小生成树的Kruskal算法。今天我们来学习一下Prim算法，来从另一个角度来理解一下这个问题。

从边到点

我们简单回顾一下Kruskal算法的原理，虽然上篇文章当中用了很多篇幅，但是原理非常简单。本质上就是我们对图中所有的边按照长度进行排序，之后我们按照顺序依次把它作为树的骨干，加入到树上来。

在此过程当中，我们为了避免导致产生环，而破坏树结构，所以使用了并查集算法来作为维护。只会考虑那些不在一个连通块中的边，否则就会构成环路。

很多人在学习了这个算法之后，会将它理解成贪心问题，或者是并查集的一个使用场景。这么理解倒也没错，但是在这个问题当中，还有更好的解释。

这个解释就是边集的扩张。

整个Kruskal运行的过程是我们不断选择边加入树中的过程，对于n个点的图来说，我们需要n-1条边。如果我们专注于这个被选出来边的集合，那么算法开始的时候，它是空集，运行结束之后，它含有n-1条边，达到饱和。

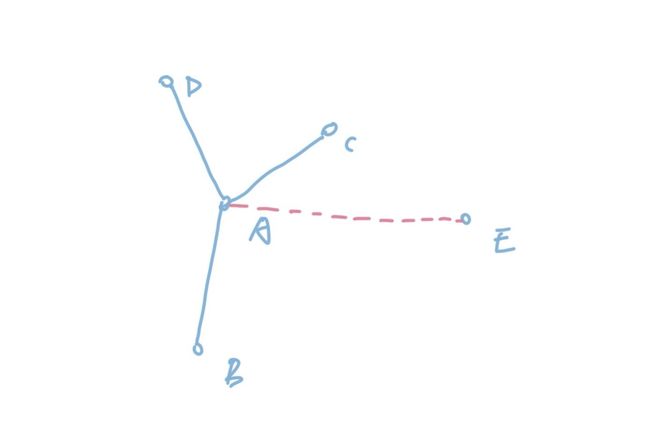
当然你也可以换个角度来看，如果我们的关注点在点上，那么最小生成树构建的过程也同样可以看成是点集的拓张。只不过点和边不同，边可以选择，但是点不可以，点只能通过选择边来覆盖。比如我们看下下图：

在图中，我们左边是一棵已经构成的树，当我们连通AE之后，我们就用边覆盖了E点。点是依托于边的，不通过边，是无法覆盖点的。

我们从空集开始，除了第一条边可以覆盖两个点之外，之后的每一条边都连通一个已经覆盖的点和一个没有覆盖的点。那么，同样也是通过n-1条边可以覆盖n个点。这个就是Prim算法的核心思路，也就是点集的拓张。

整体思路

我们明白了Prim的核心思想是点集的拓张之后就容易了，由于我们每次选择的边两边一定是一个已经覆盖的点和没有覆盖的点。所以我们生成的树是一条边一条边逐渐长大的，而不是像Kruskal那样东拼西凑起来的。

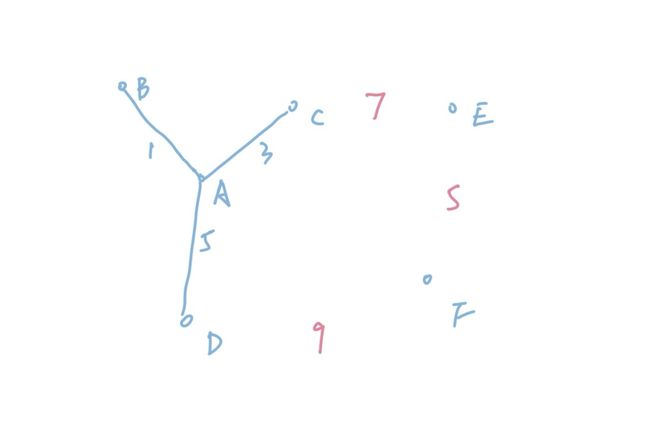
我们来看个例子：

我们已经连通了ABCD四个点，其中CE的长度是7，DF的长度是9，EF的长度是5。虽然EF的长度小于CE，但是由于我们必须要连通一个已经覆盖的点和没有覆盖的点，虽然EF的距离更小，我们也不能选择。只能选择CE，所以在整个算法运行的过程中间，这棵树是逐渐变大的。如果是Kruskal，我们肯定会先连通EF，再连通CE，整个算法运行的过程当中，各个部分都是隔开的，最后的树其实是逐渐“拼凑”出来的。

和Kruskal维护集合相比，我们维护点有没有覆盖过则要容易得多。因为树已经选择的边是不会修改的，所以我们只需要用一个数组标记一下每个位置的点有没有覆盖即可。简单的bool类型就可以实现，非常方便。

所以我们的问题只剩下了一个，如何保证我们生成出来的树的路径和最小呢？

关于这个问题的回答Prim和Kruskal一样，就是贪心。我们每次选择最小的边进行拓展，Kruskal是对所有边进行排序，然后依次判断能否选择。那么Prim算法怎么用贪心呢？

其实也很简单，我们也很容易想明白。Prim算法对边有限制，只能选择已经覆盖的点和没有覆盖的点之间的连边。我们给这些边起个名字，叫做可增广边。那么，显然我们要做的就是在可增广边当中选择一条最短的进行增广。

问题就只剩下了一个，我们怎么选择和维护这个最短的可增广边呢，难道每次拓充之后，都进行排序吗？

显然不是，因为每次都排序带来的开销太大了，我们可以用一个数据结构来维护这些边，让它们按照边的长度进行排序。这个数据结构我们应该很熟悉了，就是我们已经遇见过好几次的——优先队列。

我们排序的键也已经很明显了，就是边的长度，边是否合法的判断也很简单，我们只要判断一下是否存在没有覆盖的点即可。于是整个流程就串起来了，我们可以先来把流程理一下，写出它的流程：

选择一个点u，当做已经覆盖
把u所有相连的边加入队列
循环
    循环 从队列头部弹出边
        如果边合法
            弹出
            跳出循环
    获取边的两个端点
    将未覆盖的端点所有边加入队列
直到所有点都已经覆盖

最后，我们看下Python的实现，首先是优先队列的部分，这个逻辑我们可以利用现成的heapq来实现。

import heapq

class PriorityQueue:
  
    def __init__(self):
        self._queue = []
        self._index = 0

    def push(self, item, priority):
        # 传入两个参数，一个是存放元素的数组，另一个是要存储的元素，这里是一个元组。
        # heap内部默认从小到大排
        heapq.heappush(self._queue, (priority, self._index, item))
        self._index += 1

    def pop(self):
        return heapq.heappop(self._queue)[-1]

    def empty(self):
        return len(self._queue) == 0

然后是Prim算法的实现，这里为了存储方便，我们使用了邻接表来存储边的信息。邻接表其实是一个链表的数组，数组里的每一个元素都是一个链表的头结点。这个链表存储的是某一个节点的所有边信息。

比如邻接表中下标1的链表存储的就是与1这个节点相连的所有边的信息。这个数据结构在我们存储树和图的时候经常用到，不过也并不复杂，我们也不用真的实现一个链表，因为可以通过数组来模拟。

edges = [[1, 2, 7], [2, 3, 8], [2, 4, 9], [1, 4, 5], [3, 5, 5], [2, 5, 7], [4, 5, 15], [4, 6, 6], [5, 6, 8], [6, 7, 11], [5, 7, 9]]

if __name__ == "__main__":
    # 记录点是否覆盖
    visited = [False for _ in range(11)]
    visited[1] = True
    # 邻接表，可以理解成二维数组
    adj_table = [[] for _ in range(11)]
    # u和v表示两个端点，w表示线段长度
    # 我们把v和w放入下标u中
    # 把u和w放入下标v中
    for (u, v, w) in edges:
        adj_table[u].append([v, w])
        adj_table[v].append([u, w])

    que = PriorityQueue()

    # 我们选择1作为起始点
    # 将与1相邻的所有边加入队列
    for edge in adj_table[1]:
        que.push(edge, edge[1])

    ret = 0
    # 一共有7个点，我们需要加入6条边
    for i in range(7):
        # 如果队列为空，说明无法构成树
        while not que.empty():
            u, w = que.pop()
            # 如果连通的端点已经被覆盖了，则跳过
            if visited[u]:
                continue
            # 标记成已覆盖
            visited[u] = True
            ret += w
            # 把与它相连的所有边加入队列
            for edge in adj_table[u]:
                que.push(edge, edge[1])
            break
            
    print(ret)

结尾

到这里，关于Prim算法的介绍就结束了。其实本质上来说Prim和Kruskal是最小生成树算法的一体两面，两者的本质都是一样的，就是增广。只不过不同的是，两者一个是点的增广一个是边的增广而已。但是由于点的增广也依托于边，所以Prim当中既用到点来判断是否覆盖，又用到边的信息来增广点。

如果单纯从算法逻辑入手，没有能够理解它的本质，不仅很容易把这两个算法搞混淆，也容易在写代码的时候搞晕，不知道到底要维护什么，要拓展什么。

增广的思想在图论相关的算法当中经常用到（比如网络流），并不只是在最小生成树当中出现，因此理解这一概念对于我们后续的学习非常重要。希望大家都能领会其中的精髓。

今天的文章就到这里，原创不易，扫码关注我，获取更多精彩文章。