算法笔记---问题 A: 关键路径

题目描述

图的连接边上的数据表示其权值，带权值的图称作网。

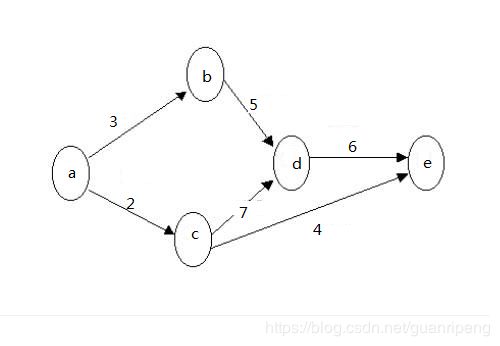
图可描述为顶点集为（a,b,c,d,e)

边集及其权值为(始点，终点 权值）：

a b 3
a c 2 
b d 5
c d 7
c e 4
d e 6    

网的源点是入度为0的顶点，汇点是出度为0的顶点。网的关键路径是指从源点到汇点的所有路径中，具有最大路径长度的路径。上图中的关键路径为a->c->d->e，其权值之和为关键路径的长度为15。

本题的要求是根据给出的网的邻接矩阵求该网的关键路径及其长度。

输入：

第一行输入一个正整数n（1<=n<=5)，其代表测试数据数目，即图的数目
第二行输入x(1<=x<=15)代表顶点个数，y(1<=y<=19)代表边的条数
第三行给出图中的顶点集，共x个小写字母表示顶点
接下来每行给出一条边的始点和终点及其权值，用空格相隔，每行代表一条边。

输出：

第一个输出是图的关键路径（用给出的字母表示顶点， 用括号将边括起来，顶点逗号相隔）
第二个输出是关键路径的长度
每个矩阵对应上面两个输出，两个输出在同一行用空格间隔，每个矩阵的输出占一行。

样例：

输入：
2
5 6
abcde
a b 3
a c 2
b d 5
c d 7
c e 4
d e 6
4 5
abcd
a b 2
a c 3
a d 4
b d 1
c d 3
输出：
(a,c) (c,d) (d,e) 15
(a,c) (c,d) 6

解题思路：

求关键路径的题一般都是有向无环图，且都是AOE（Activity On Edge）网
即图中的顶点表示事件，图中的边表示活动。
关键路径共有四部分需要求出来：
1、事件的最早发生时间
2、事件的最晚发生时间
3、活动的最早开始时间
4、活动的最晚开始时间

1、事件最早发生的时间，是从前往后顺序计算，取最大值
即ve[v] = max{ve[top] + weight}

2、求出事件的最迟发生时间，是从后往前顺序计算，取最小值
vl[top] = min{vl[v] - weight}

3、活动的最早开始时间 = 事件的最早发生时间

4、活动的最晚开始时间 = 事件的最晚发生时间 - 该活动所需时间

5、判断活动的最早开始时间和最晚开始时间是否一样，两个时间相同则表示该活动为关键路径上的活动。

下图为王道考研2020的知识点：

注意：

该题在输出关键路径的时候，需要找出图中的源点，不然可能不会通过测试数据。

下面为AC代码：

/*
 * @Description: 关键路径
 */
#include 
#include 
#include 
#include 
#include 
#include
using namespace std;
struct path_node
{
    int v; //表示弧头结点 即 a -> b 此时 v 表示 b；
    int weight;
    path_node(int v, int weight)
    {
        this->v = v;
        this->weight = weight;
    }
};

const int path_max_num = 20; //最大边数或者结点数
int n, x, y;                 //n表示图的数目，x表示结点数，y表示边的数目
vector<path_node> G[path_max_num];
int in_depth[path_max_num];             //入度数组
string vertex;                          //表示结点集合
int ve[path_max_num], vl[path_max_num]; //事件最早发生时间，事件最晚发生时间
stack<int> top_order;//表示拓扑序列
vector<int> path[path_max_num];//关键路径

/**
 * @description: 找出 ch 在 vertex 中的位置
 * @param : 当前结点的值
 * @return: ch 的位置
 */
int find_id_in_vertix(char ch)
{
    return vertex.find(ch);
}

//拓扑排序
bool topology_sort()
{
    fill(ve, ve + path_max_num, 0);
    fill(in_depth,in_depth + path_max_num,0);
    queue<int> q;
    //求出各个结点的入度
    for (int i = 0; i < x; i++)
    {
        for (int j = 0; j < G[i].size(); j++)
        {
            path_node node = G[i][j];
            in_depth[node.v]++;
        }
    }

    for (int i = 0; i < x; i++)
    {
        if (in_depth[i] == 0)
        {
            q.push(i);
        }
    }
    
    while (!q.empty())
    {
        int top = q.front();
        q.pop();
        top_order.push(top);
        for (int i = 0; i < G[top].size(); i++)
        {
            path_node node = G[top][i];
            int v = node.v;
            int weight = node.weight;
            in_depth[v]--;
            if (in_depth[v] == 0)
            {
                q.push(v);
            }
            //求出事件最早发生的时间，此时取最大值,从前往后顺序计算
            //ve[v] = max{ve[top] + weight}
            if (ve[top] + weight > ve[v])
            {
                ve[v] = ve[top] + weight;
            }
        }
    }
    if (top_order.size() != x)
    {
        return false; //表示当前的图不是有向无环图
    }
    return true;
}

//求出关键路径
int critical_path()
{
    if (topology_sort() == false)
    {
        //表示没有拓扑序列
        return -1;
    }
    //初始化 vl 数组
    int max_length = 0;
    for(int i = 0;i < x;i++){
        if(ve[i] > max_length){
            max_length = ve[i];
        }
    }
    fill(vl, vl + path_max_num, max_length);
    //直接使用top_order求出事件的最迟发生时间
    while (!top_order.empty())
    {
        int top = top_order.top();
        top_order.pop();
        for (int i = 0; i < G[top].size(); i++)
        {
            path_node node = G[top][i];
            int v = node.v;
            int weight = node.weight;
            //求出事件的最迟发生时间，此时取最小值，从后往前顺序计算
            //vl[top] = min{vl[v] - weight}
            if (vl[v] - weight < vl[top])
            {
                vl[top] = vl[v] - weight;
            }
        }
    }
	//初始化关键路径的数组
    for(int i = 0;i < x;i++){
        path[i].clear();
    }
    //遍历邻接表的所有边
    //计算活动的最早开始时间和最晚开始时间
    for (int i = 0; i < x; i++)
    {
        for (int j = 0; j < G[i].size(); j++)
        {
            path_node node = G[i][j];
            int v = node.v;
            int weight = node.weight;
            //活动的最早开始时间 e
            //活动的最晚开始时间 l
            int e = ve[i];          //活动的最早开始时间 = 事件的最早发生时间
            int l = vl[v] - weight; // 活动的最晚开始时间 = 事件的最晚发生时间 - 该活动所需时间
            //如果活动的最早开始时间等于活动的最晚开始时间
            if (e == l)
            {
                //表示当前结点为关键路径的结点
                //printf("(%c,%c) ", vertex[i], vertex[v]);
                //cout << "(" << vertex[i] << "," << vertex[v] << ")" << " ";
                path[i].push_back(v);
            }
        }
    }
    //求出源点
    int s;
    for(int i = 0;i < x;i++){
        if(ve[i] == 0){
            s = i;
            break;
        }
    }
    while(path[s].size()){
        printf("(%c,%c) ",vertex[s],vertex[path[s][0]]);
        s = path[s][0];
    }
    
    return max_length;
}

int main()
{
    cin >> n; //表示共有几个网络
    char u_ch, v_ch; //表示起始结点和终止结点 u_ch -> v_ch
    int weight;      //边的权值
    while(n--){
        cin >> x >> y; //顶点的个数为x，边数为y
        cin >> vertex; //表示结点的集合
        for (int i = 0; i < x; i++)
        {
            G[i].clear(); //初始化图
        }

        for (int i = 0; i < y; i++)
        {
            cin >> u_ch >> v_ch >> weight;
            int u = find_id_in_vertix(u_ch);
            int v = find_id_in_vertix(v_ch);
            G[u].push_back(path_node(v, weight));
        }
        int path_length = critical_path();
        cout << path_length << endl;
    }
    //system("pause");
    return 0;
}