TOF双频去距离模糊原理

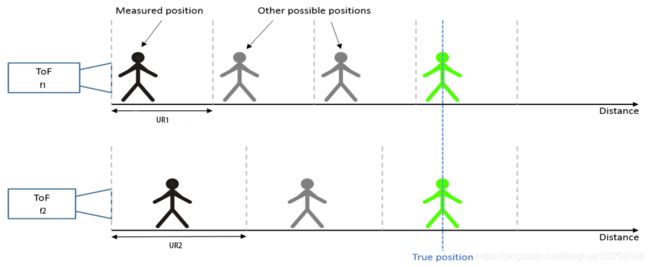
1. TOF距离模糊现象及原因

Continuous-Wave TOF (CW-TOF)法通过测量发射波与接收波的相位差来计算距离。假设相位差为phi, 调制频率为f_m, 则距离值计算为：
$$d=\frac{c}{2f_m}\ast (\frac{\varphi }{2\pi }+k)$$
式中，c为光速，约为3*10⁸m/s, k为正整数，代表整数周期的个数。如果仅仅使用一种调制频率进行距离测量，无法确认真实距离落在第几个距离周期，即无法确认k值，这种现象称为TOF测距的距离模糊现象，通常一次测量中默认k=0。
在调制频率为f_m时，整个周期的距离称之为当前调制频率下的模糊距离( Unambiguous Range)：
$$UR=\frac{c}{2f_m}$$

2. 双频测量

解决TOF距离模糊的一种方法为双频测量，即对着同一个物体使用两种不同的频率进行测量，通过两次测量结果确定出真实距离。
假设频率为$f_A$时的测量相位为${\varphi }_A$， 频率为$f_B$时的测量相位为${\varphi }_B$， 那么$f_A$时的最大测量距离$d_{uA}=\frac{c}{2f_A}$，$f_B$时的最大测量距离$d_{uB}=\frac{c}{2f_B}$。
将$f_A：f_B$转化为两个互为质数的整数对的比值$M_A：M_B$。
另外假设${\varphi }_A$对应的模糊次数为$n_A$, ${\varphi }_B$对应的模糊次数为$n_B$,则$n_A$的范围为0~M_A-1, $n_B$的范围为0~M_B-1。
另外将相位转换到[0, 1)的范围内，有：$P_A=\frac{{\varphi }_A}{2\pi }$, $P_B=\frac{{\varphi }_B}{2\pi }$。
真实距离$d$可计算为：
$$d=d_{uA}(n_A+P_A）=d_{uB}(n_B+P_B）$$
只有知道了$n_A$或者$n_B$的值才可以得到$d$。

当$n_A$与$n_B$的值正确时，$|d_{uA}(n_A+P_A)-d_{uB}(n_B+P_B)|$的值最小，又$d_{uA}\propto \frac{1}{f_A}\propto \frac{1}{M_A}$，$d_{uB}\propto \frac{1}{f_B}\propto \frac{1}{M_B}$，因此可以将$n_A$与$n_B$的求解转化为下式的最小值：
$$y(n_A,n_B)=|M_B\ast (n_A+P_A)-M_A\ast (n_B+P_B)|$$
最终$d$计算为：
$$d=\frac{c}{2}\ast [\frac{w\ast (n_A+P_A)}{f_A}+\frac{(1-w)\ast (n_B+P_B)}{f_B}]$$

下面以一个实例对上面所述方法进行验证。假设测量结果有：
$f_A=40Mhz$时，$d_{uA}=\frac{c}{2f_A}=3.75m$，测得的距离为1.5m；
$f_B=30Mhz$时，$d_{uB}=\frac{c}{2f_B}=5.00m$，测得的距离为4.0m；
此时有:
$$P_A=\frac{d_A\ast 2f_A}{c}=\frac{1.5\ast 2\ast 40\ast 10^6}{3\ast 10^8}=0.4$$
$$P_B=\frac{d_B\ast 2f_B}{c}=\frac{4.0\ast 2\ast 30\ast 10^6}{3\ast 10^8}=0.8$$
设$M_A=4,M_B=3$， 则$(n_A,n_B)=|M_B\ast (n_A+P_A)-M_A\ast (n_B+P_B)|=|3\ast (n_A+0.4)-4\ast (n_B+0.8)|=|3\ast n_A-4\ast n_B-2|$
又$n_A\in [0，3]$, $n_B\in [0,4]$ , 可算得当$n_A=2$, $n_B=1$时，$y(n_A,n_B)$的值最小。
此时，$d_{uA}(n_A+P_A)=3.75\ast (2+0.4)=9m$, $d_{uB}(n_B+P_B)=5.0\ast (1+0.8)=9m$，最终得到的真实距离$d=9m$。

另一种更直接的方法可以使用三步计算出真实距离。
第一步，利用一种称之为modified Chinese remainder theorem 的方法估算$n_B$:
$e=P_A\ast M_B-P_B\ast M_A$
$n_B=mod[k0\ast round(e),M_B]$
其中，k0满足$mod(k0\ast M_A,M_B)=1$的最小整数。
第二步，生成一个临时变量X：
$X=w\ast M_B\ast (n_A+P_A)+(1-w)\ast M_A\ast (n_B+P_B)$
$=M_A\ast n_B+M_A\ast P_B+w\ast (e-round(e))$
本质上X是上文中$d$的最终计算公式的另一种表达形式。
第三步，计算出真实距离d:
$$d=d_E\ast \frac{X}{M_A\ast M_B}=\frac{c}{2\ast gcd(f_A,f_B)}\ast \frac{X}{M_A\ast M_B}$$

继续前例来说明：
step1:
$e=0.4\ast 3-0.8\ast 4=1.2-3.2=-2$
$mod(k0\ast 4,3)=1$， 从而$k0=1$
$n_B=mod(-2,3)=1$
step2:
$X=M_A\ast n_B+M_A\ast P_B+w\ast (e-round(e))=4\ast 1+4\ast 0.8+0=7.2$
step3:
$d_E=\frac{c}{2gcd(f_A,f_B)}=\frac{3\ast 10^8}{2\ast 10\ast 10^6}=15$
$d=d_E\ast \frac{X}{M_A\ast M_B}=15\ast \frac{7.2}{4\ast 3}=9m$

参考资料：
[1]A. P. P. Jongenelen, D. G. Bailey, A. D. Payne, A. A. Dorrington, and D. A. Carnegie, “Analysis of errors in ToF range imaging with dual-frequency modulation,” Instrumentation and Measurement, IEEE Transactions on 60.5 (2011): 1861-1868.