算法竞赛宝典-递推算法

算法竞赛宝典-递推算法

Problem A
【递推】挖地雷 待更新

问题 B: 【递推】偶数３的个数

时间限制: 1 Sec 内存限制: 64 MB
题目描述
“报告，我军已探出地雷阵中所有的地雷位置，并且还发现了一份使用说明书。”一个黑暗军团的小兵匆忙跑来，交给修罗王一张纸。

只见这张纸上面写道：“我是一颗萌萌的地雷，拆除我很容易，看到我身上标着的整数Ｎ了吗？你只要输入这个Ｎ位数中有多少个数中有偶数个数字3就可以把我拆除哦，加油！你行的。”

输入
一个整数Ｎ。

输出
输出这个Ｎ位数中有多少个数中有偶数个数字３。

样例输入
2
样例输出
73

思路
对每一位数字而言，有两种选择：3或非3，非3的选择有9种方案（特别地，最高位只有8种）
因此使用数组存储i位数时 奇数个3与偶数个3的数量，转移一下即可
转移方法：偶数=偶数并且新一位不是3+奇数并且新一位是3
奇数=奇数并且新一位不是3+偶数并且新一位是3

#include 
using namespace std;
typedef long long ll;
const int N=3e5+5;
const int mod=10000;
int a[N],b[N];
int main()
{
    int n;
    scanf("%d",&n);
    if(n==1)
    {
        printf("9");
        return 0;
    }
    a[1]=8;
    b[1]=1;
    for(int i=2;i<=n;i++)
    {
        a[i]=a[i-1]*9+b[i-1];
        b[i]=a[i-1]+b[i-1]*9;
    }
    printf("%d",a[n]);
    return 0;
}

问题 C: 【递推】布阵

时间限制: 1 Sec 内存限制: 64 MB
题目描述
黑暗军团在城外的草地上布阵，如果把草地划分成很多大小一样的方格，看成无限大的棋盘，军团从中心点出发，每次只能向上或向左或向右移动一步（移动的过程中，走过的格子不能再次进入）。就能到达相邻的一个格子里，如果一共移动了N步，总共有多少种走法呢？

输入
一个整数即Ｎ，N≤30。

输出
输出步数。

样例输入
2
样例输出
7

思路：
移动共有上，左，右三种，我将其划分为上移（向上）和平移（左/右）两大类。
由于我们不能移动回已经走过的位置，平移操作方向一旦确定，便只可能向一个方向移动。也就是说，进行过平移操作的状态的下一步如果选择平移操作，方向是唯一确定的，而当上一步操作进行的是上移操作的时候，平移可以从左右两个方向当中选择一个。
而上移操作不受上述条件限制，任何一个状态皆可进行上移操作。
下面的代码中，数组a存储平移，数组b存储上移。
初始状态：2种平移1种上移。

#include 
using namespace std;
typedef long long ll;
const int N=3e2+5;
const int mod=10000;
ll a[N],b[N];
int main()
{
    int n;
    scanf("%d",&n);
    a[1]=2;
    b[1]=1;
    for(int i=2;i<=n;i++)
    {
        a[i]=a[i-1]+b[i-1]*2;
        b[i]=a[i-1]+b[i-1];
    }
    printf("%lld",a[n]+b[n]);
    return 0;
}

问题 D: 【递推】极值问题

时间限制: 1 Sec 内存限制: 64 MB
题目描述
修罗王：“等了这么久，怎么攻城的魔法炮还没有响？”

邪狼满头大汗：“这魔法炮使用起来太复杂了，每次操作都需要输入验证码，首先它会产生一个正整数k，你要根据这个数输入正确的m和n两个整数才能发射。”

修罗王：“这是谁设计的炮啊，不考虑客户体验，界面友好性吗？让我来看看…”

现已知m，n为整数，且满足下列两个条件：

（1）m、n属于{1，2，…，k}，即1≤m，n≤k

（2）（n²－mn－m²）²=1

你的任务是：根据输入的正整数k(1≤k≤109)，求一组满足上述两个条件的m、n，并且使m2+n2的值最大。例如从键盘输入k=1995，则输出m=987 ，n=1597。

样例输入
1995
样例输出
987 1597

思路
用n=m+k代入条件2，将表达式化简可以化简成(k²+mk-m²)²=1，平方内所有项取负号可得到与条件2相同的式子，因此符合条件的数列即为斐波那契数列，只需找到斐波那契数列当中最大的比n小的连续两项即可。

#include 
using namespace std;
typedef long long ll;
const int N=3e2+5;
const int mod=10000;
int main()
{
    int n,a=1,b=1;
    scanf("%d",&n);
    while(a+b<=n)
    {
        int tmp=b;
        b=a+b;
        a=tmp;
    }
    printf("%d %d",a,b);
    return 0;
}

问题 E: 【递推】区域划分问题

时间限制: 1 Sec 内存限制: 64 MB
题目描述
已知黑暗军团的魔法炮发射轨迹成直线，现有n座魔法炮产生n(n≤500)条直线将地面（可视为平面，因为魔法炮具有降维属性，即可将三维空间降为二维空间）分割成了许多区域，并且已有p（p≥2）条直线相交于同一点，问n条直线最多能将平面分割成多少个不同的区域？

输入
输入一个数n和p。

输出
输出分割的区域数。

样例输入
3 2
样例输出
7
思路
先考虑交于同一点的p条直线，共将平面分成p*2个区域，然后往这个平面增加n-p条直线。每一条直线可以被当前k条直线截成k+1段，就多分成k+1个区域。递推即可得到结果。

#include 
using namespace std;
typedef long long ll;
const int N=3e2+5;
const int mod=10000;
int main()
{
    int n,p;
    scanf("%d%d",&n,&p);
    int ans=p*2;
    for(int i=n-p,j=p+1;i>0;i--,j++)
        ans+=j;
    printf("%d",ans);
    return 0;
}

问题 F: 【递推】军事情报

时间限制: 1 Sec 内存限制: 64 MB
题目描述
俗话说，“不怕神一样的对手，就怕猪一样的队友。”虽然后世的历史学家们总是对修罗王的黑暗军团最终以惨败告终的原因争吵不休，但有一个原因是大家公认的，那就是邪狼把Ｎ封军事情报装在Ｎ个信封时，他居然全部都装错了信封。不管你信不信，反正我是信了，现求所有情报都装错信封共有多少种可能？

输入
一个整数N，1

输出
一个整数，即可能数。

样例输入
2
样例输出
1

思路
由于所有情报都装错了信封，那么对于第一个信封，除了应装的一个情报，总共有n-1种可能。而对于每一种可能性，不妨设第一个信封装了第k个情报，则第k个信封可以分成两种情况：1.装有第一个情报，此时可能出现的情况数就是剩余n-2个信封都装错的情况数，即a[n-2]；2.不是装有第一个情报。此时对于除去第一个信封以外的n-1个信封，第一个情报与第k个情报等效，出现的情况数即为除去第一个信封后n-1个信封都装错的情况数，即a[n-1]。因此递推式可推导。

#include 
using namespace std;
typedef long long ll;
const int N=3e2+5;
const int mod=10000;
int n;
ll a[N];
int main()
{
    scanf("%d",&n);
    a[1]=0;
    a[2]=1;
    for(int i=3;i<=n;i++)
        a[i]=(i-1)*(a[i-1]+a[i-2]);
    printf("%lld",a[n]);
    return 0;
}

问题 G: 【递推】密文传送

时间限制: 1 Sec 内存限制: 64 MB
题目描述
黑暗军团的情报采用密文传输，即把一些有规律的单词编成数字。其原理是：字母表中共有26个小写字母{a，b，…，z}，这些特殊的单词长度不超过20且字母按升序排列。把所有这样的单词放在一起，按字典顺序排列，一个单词的编码就对应着它在字典中的位置。例如：a→1， b→2， z→26， ab→27， ac→28。

你的任务就是对于所给的单词，求出它的编码。

输入
仅一行，被编码的单词。

输出
仅一行，对应的编码。如果单词不在字母表中，输出0。

样例输入
ab
样例输出
27

这个题不应该放在组合数学里面吗，怎么跑出来了
因为长度不超过20，数据很小，题目中也没说取模的事情，可以放心大胆的用除法了做的暴力一点

#include 
#include 
#include 
using namespace std;
typedef long long ll;
ll qpow(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1) ans=ans*a;
        a=a*a;
        b>>=1;
    }
    return ans;
}
ll C(ll x,ll y)
{
    if(y==0||y==x) return 1;
    if(x<y) return 0;
    ll a=1,b=1;
    for(int i=1;i<=min(y,x-y);i++)
    {
        a=a*i;
        b=b*(x-i+1);
    }
    return b/a;
}
int main()
{
    char ch[20];
    scanf("%s",ch);
    int n=strlen(ch);
    ll ans=0;
    for(int i=1;i<n;i++)
        ans+=C(26,i);
    char a='a'-1;
    for(int i=0;i<n;i++)
    {
        if(ch[i]<=a)
        {
            printf("0");
            return 0;
        }
        for(char j=a+1;j<ch[i];j++)
            ans+=C('z'-j,n-i-1);
        a=ch[i];
    }
    printf("%lld",ans+1);
    return 0;
}

问题 H: 【递推】标准汉诺塔问题

时间限制: 1 Sec 内存限制: 64 MB
题目描述
楚继光报怨道：“能量盘为什么要这样移动？真够麻烦的。”

“因为这样移动，暗含宇宙运行的奥义，它能够产生巨大的魔法力，将修罗王的魔法炮阵灭成渣。”墨老师一副高深莫测的神情。

如图所示，已知魔法学院的防御系统的能量模块上有三根柱子a，b，c，能量盘为中间有孔的圆盘状，能量盘直径依次递减，初始时b柱、c柱为空，所有盘片套在a柱上，并且上面的盘片总是比下面的盘片小，现需将a柱上的能量盘通过b柱移到c柱上，规则是每次移动只能移动最上面的能量盘，而且保持任何柱子上的能量盘的排列均是上面的盘片比下面的盘片要小。试问需要移动多少次？

输入
一个整数n，表示n个盘。

输出
一个整数，表示需要移动的次数。

样例输入
2
样例输出
3
思路：汉诺塔结论 移动次数为$2^n-1$
要是推一下的话…
就是每次移动可以拆分成三部分：将n-1个盘从初始柱移动到中间柱，再将最下面的一个移动到目标柱，再将n-1个移动到目标。第一步和第三步的步骤数相同，都是$a_{n-1}$，第二步仅需一步，则可得到递推式$a_n=2a_{n-1}+1$，再有$a_1=1$ 可得通项式$a_n=2^n-1$
这里计算用的快速幂，其实也可以直接使用位运算的

#include 
using namespace std;
typedef long long ll;
const int N=3e5+5;
ll qpow(ll x,ll y)
{
    ll ans=1;
    while(y)
    {
        if(y&1) ans=ans*x;
        x=x*x;
        y>>=1;
    }
    return ans;
}
int main()
{
    ll n;
    scanf("%lld",&n);
    printf("%lld",qpow(2,n)-1);
    return 0;
}

问题 I: 【递推】Hanoi双塔问题

时间限制: 1 Sec 内存限制: 64 MB
题目描述
楚继光：“防御系统还真有用，修罗王的魔法炮阵的火力果然减弱了，但好像还差一点点啊？”

墨老师：“哦，是吗，那试试双塔防御体系吧。”

如图所示，给定A，B，C三根足够长的细柱，在A柱上放有2n个中间有空的能量圆盘，共有n个不同的尺寸，每个尺寸都有两个相同的圆盘，注意这两个圆盘是不加区分的，图为n=3的情形。现要将这些圆盘移到C柱上，在移动过程中可放在B柱上暂存。每次只能移动一个圆盘，每个柱子的圆盘保持上小下大的顺序。要求输出最少移动次数。

输入
一个正整数，表示A柱上有2n个圆盘。

输出
仅一行，包含一个正整数，为最少移动次数。

样例输入
2
样例输出
6

提示
对于100%数据，1≤n≤200。
其实就是把汉诺塔的事情做两遍…
但是由于数据较大，会超过longlong最大值，这里使用的java的biginteger。

import java.math.BigInteger;
import java.util.Scanner;
 
public class Main {
 
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt();
        BigInteger x=BigInteger.valueOf(2);
        System.out.println(x.pow(n).subtract(BigInteger.ONE).multiply(BigInteger.valueOf(2)));
    }
}

问题 J: 【递推】四塔问题

时间限制: 1 Sec 内存限制: 64 MB
题目描述
墨老师：“现在可以了吗？”

楚继光：“开始是压制住了修罗王的魔法炮阵，但现在修罗王又加强了火力。”

墨老师：“那就用四塔防御系统好了。”

四塔防御系统一共有4根柱子，而不是3根，那么至少需要移动能量盘多少次，才能把所有的能量盘从第1根柱子移动到第4根柱子上呢？

为了编程方便，你只需输出这个结果%10000的值。

输入
含有多组测试数据，每组一个正整数N。（0

输出
一个正数，表示把N个能量盘从第1根柱子移动到第4根柱子需要的最少移动次数%10000的值。

样例输入
15
样例输出
129

其实下面这段在比赛场上完全可以打个表猜出来

现在有四个柱子，类比三个柱子的汉诺塔，我们可以将移动过程分成三步：先用四个柱子把x个盘从起始搬到中间的其中一个，再用三个柱子将剩下的n-x个盘搬到目标位置，再把前面x个盘搬到目标位置。
我们已知中间步骤为汉诺塔的操作，而前后两步骤步骤数相同，并且可以使用之前的结论。
$a[n]=2\cdot a[x]+2^{n-x}-1$
关键在于：如何对n个盘进行划分，分成这两个步骤。
假设我们知道了m个盘时的划分方法，即$x=x_m$时划分最优，无论x增加/减少都不会使划分更优
则m+1个盘时的划分方法可在m个盘的基础上进行讨论：
1.$a[m+1]=2\cdot a[x+1]+2^{m-x}-1$
2.$a[m+1]=2\cdot a[x]+2^{m-x+1}-1$
因此，可以求出两种方案的差值：
1.$a[m+1]-a[m]=2\cdot (a[x+1]-a[x])$
2.$a[m+1]-a[m]=2^{m-x+1}-2^{m-x}=2^{m-x}$
只要分析出两种方案差值的大小关系，就可以得到划分方法的选取方案了。
为了寻找规律， 我默认在可以选取方案1时优先选择方案1，仅当选取方案1的答案大于方案2才选取方案2。

我们先列出前几项数列的值： 1 3 5 9 13 17 25
再写出相邻两项的差：2 2 4 4 4 8

3=2*1+1
5=2*1+3（方案2）
9=2*3+3
13=2*5+3
17=2*5+7（方案2）
25=2*9+7...

假设我们按照使用方案2将上述序列划分层次，那么每一层增长的大小相同，并且使用方案1的次数为上一层的数的个数。而每一层多一次使用方案2，即每一层的个数成等差数列递增，我就是使用的这个性质求得的答案。

#include 
using namespace std;
typedef long long ll;
const int N=3e5+5;
const int mod=10000;
int a[N];
int main()
{
    ll n;
    scanf("%lld",&n);
    a[1]=1;
    for(int i=2,p=2,q=2,k=2;i<=n;i++,q--)
    {
        if(q==0) q=++p,k=k*2%mod;
        a[i]=(a[i-1]+k)%mod;
    }
    printf("%d",a[n]);
    return 0;
}

问题 K: 【递推】妖兽特攻队

时间限制: 1 Sec 内存限制: 64 MB
题目描述
不甘心失败的修罗王派出大小各不相同的一队妖兽站在河左岸的石墩（记为A）上，要过到对岸的石礅（记为D）上去执行军事任务。如图8.11所示，河心有几片荷叶（分别记为Y1…Ym）和几个石墩（分别记为S1…Sn）。

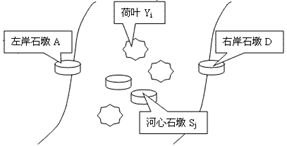
妖兽站队和移动方法规则如下：

（１）每只妖兽只能站在荷叶、石墩或者比它大一号的妖兽背上（统称为合法的落脚点）；

（２）一只妖兽只有背上没有其他妖兽的时候才能够从一个落脚点跳到另一个落脚点；

（３）妖兽允许从左岸A直接跳到河心的石墩、荷叶和右岸的石墩D上，允许从河心的石墩和荷叶跳到右岸的石墩D上；

（４）妖兽在河心的石墩之间、荷叶之间以及石墩和荷叶之间可以来回跳动；

（５）妖兽在离开左岸石墩后，不能再返回左岸；到达右岸后不能再跳回；

（６）假定石墩承重能力很大，允许无论多少只妖兽都可待在上面。但是由于石墩面积不大，至多只能有一只妖兽直接站在上面，而其他的妖兽只能依规则1落在比它大一号的妖兽背上；

（７）荷叶不仅面积不大，而且负重能力也有限，至多只能有一只妖兽站在上面；

（８）每一步只能移动一只妖兽，并且移动后需要满足站队规则；

（９）在一开始的时候，妖兽均站在A上，最大的一只妖兽直接站在石墩上，而其他的妖兽依规则6站在比其大一号的妖兽背上。

妖兽希望最终能够全部移动到D上，并完成站队。

设河心有M片荷叶和N个石墩，请求出这队妖兽至多有多少只，在满足站队和移动规则的前提下，能从A过到D。

例如当河心有一片荷叶和一个石墩时，此时最多有4只妖兽跳动9步能够过河。如图所示。

样例输入
1
1
样例输出
4

每个荷叶只能承载一个妖兽，而将石墩编号后，i个石墩能承载的就是前i-1个石墩承载的妖兽总和+荷叶承载的妖兽总和。最终所求答案就是前n个石墩承载的妖兽总和+荷叶承载的妖兽总和，即为假定存在第n+1号石墩时，其能承载的妖兽数。

#include 
using namespace std;
typedef long long ll;
const int N=3e5+5;
const int mod=10000;
ll a[N];
int main()
{
    int m,n;
    ll sum=0;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n+1;i++)
    {
        a[i]=sum+m+1;
        sum+=a[i];
    }
    printf("%lld",a[n+1]);
    return 0;
}

问题 L: 【递推】曲线分割

时间限制: 1 Sec 内存限制: 64 MB
题目描述
设有n条封闭曲线画在平面上，而任何两条封闭曲线恰好相交于两点，且任何三条封闭曲线不相交于同一点，问这些封闭曲线把平面分割成的区域个数。

输入
输入整数n。

输出
输出分割的区域个数。

样例输入
2
样例输出
4

每一条曲线可被前n-1条曲线交于（n-1）*2个点，即被分成（n-1）*2段，新增（n-1）*2个空间。

#include 
using namespace std;
typedef long long ll;
const int N=3e2+5;
const int mod=10000;
int n,a[N];
int main()
{
    scanf("%d",&n);
    a[1]=2;
    for(int i=2;i<=n;i++)
        a[i]=a[i-1]+(i-1)*2;
    printf("%d",a[n]);
    return 0;
}

Problem M
【递推】实数数列 待更新