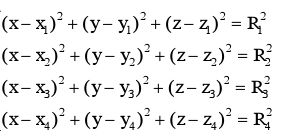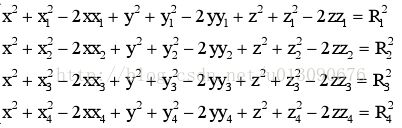ibeacon UWB GPS 空间四点定位算法

最近在研究uwb空间四点的精准定位，其实是基于RSSI原理的，蓝牙IBEACON,GPS也差不多基于这个原理

三维空间的四点定位算法：

已知四个基站点的坐标(x1,y1,z1)(x2,y2,z2)(x3,y3,z3)(x4,y4,z4)和到未知点(x,y,z)的距离R1,R2,R3,R4

所以四点定位使用矩阵求解方程的方式：

其中要求的点的坐标是(x,y,z)，已知的四个探针的位置为(x1,y1,z1)，(x2,y2,z2)，(x3,y3,z3)，(x4,y4,z4)，r1到r4为所求的点到四个探针的距离。

现在我们的任务就是求解上述方程，首先分解：

然后相减：

其中：

这时候就可以转换为矩阵相乘:

假设上面矩阵为A*B=C，那么此时只需要求解A的逆矩阵，然后把逆矩阵同时乘以等式两边，就可以求得x，y，z了。

具体求解逆矩阵的方法为高斯-约旦消元法

 

高斯-约旦消元法原理

假设 AX=E ，其中， A 为 n 阶系数矩阵（与上面的解线性方程组对照）；E 为单位矩阵，即

，其中

为单位列向量； X 为 n 个列向量构成的矩阵，即

，其中

为列向量。于是，可以把等式 AX=E 看成是求解 n 个线性方程组

，求出了所有的

之后，也即得到了矩阵 X。而由 AX=E 可知，矩阵 X 是 A 的逆矩阵，即

。这样，就求出了 A 的逆矩阵了。于是，求逆矩阵的过程被化成了解线性方程组的过程，因此我们可以用 Gauss-Jordan 消元法来求逆矩阵。求逆矩阵时，系数矩阵 A 和单位矩阵 E 可以共用一块存储区，在每一次约化过程中，系数矩阵逐渐被其逆矩阵替代。

示例

有如下的方程组：

显而易见，该方程组对应的系数矩阵 A 和右端向量矩阵 B（此处只有一个右端向量）分别为：

其实在求逆矩阵的过程中，矩阵 B 无关紧要，可以忽略，不过此处还是把它写出来了。下面，把单位矩阵 E 附在 A 的右边，构成另一个矩阵（A|E）：

下面，通过矩阵的初等变换，将 A 化为单位矩阵 E，而 E 则化为了 A 的逆矩阵。以下是转化步骤：

（1）主元选为 3，所以将 Row1 （第一行）与 Row2 （第二行）交换：

（2）主元所在行的所有元素除以主元：

（3）Row1 – Row2 ，Row3 – 2 × Row2 ：

现在，原来的矩阵 A 有一列被化为了单位阵的形式。

（4）重新选主元，这一次主元选为 5/3，于是 Row1 ÷ 5/3 （主元所在行的所有元素除以主元）：

（5）Row2 – (1/3) × Row1 ，Row3 – (4/3) × Row1 ：

现在，原来的矩阵 A 又有一列被化为了单位阵的形式。

（6）重新选主元，这一次主元选为 -1/5 ，于是 Row3 ÷ (-1/5) （主元所在行的所有元素除以主元）：

（7）Row1 – (2/5) × Row3 ，Row2 – (1/5) × Row3 ：

现在，原来的矩阵 A 的所有列都被化为了单位阵的形式。可见，以上过程非常适合于计算机编程求解。至此，我们完成了从 A 到 E 的转换，这个过程中使用了选主元的方法，但没有使用列交换。于是，原来的单位矩阵 E 就变成了

，即：

 

关键部分的C++代码：

/**
 * G-J消元法求矩阵逆矩阵
 *
 * @param 
 * @return 一个矩阵对象，为当前的矩阵的逆矩阵
 */
Matrix Matrix::inverseGJ(){
    int i,j,k;
    int dimension = row;
    Matrix output(row,col);
    //将输出矩阵初始化为单位矩阵
    output.eye();
 
    for(i=0;i     {
        for(j=0;i         {
            if(pmm[j*col+i]!=0)
            {
                swap(0,j);
                output.swap(0,j);
                break;
            }
        }
        for(j=0;j         {
            if(j==0)  //如果是第一行，将input[j][i]设置为1，其他元素均除以input[i][i]
            {
                for(k=dimension-1;k>=0;--k)
                    output.setElement(j,k,output.getElement(j,k)/pmm[j*col+i]);
                for(k=dimension-1;k>=i;--k)
                    pmm[j*col+k]/=pmm[j*col+i];
            }
            else  //如果不是第一行，将每一行的input[j][i]设置为0，该行其他元素都要倍数的减去第一行对应位置上的值
            {
                for(k=dimension-1;k>=0;--k)
                    output.setElement(j,k,output.getElement(j,k)-pmm[j*col+i]/pmm[i]*output.getElement(0,k));
                for(k=dimension-1;k>=i;--k)
                    pmm[j*col+k]=pmm[j*col+k]-pmm[j*col+i]/pmm[i]*pmm[k];
            }
        }
        swap(0,(i+1)%dimension);  //每次都将下一次需要处理的行和当前的第一行交换
        output.swap(0,(i+1)%dimension);
    }
    output.reorder(); //因为之前的交换操作，行顺序乱了，需要重新排列一下，即把第一行的数据放到最后一行后面
    
    return output;
}

具体C++代码请加微信：