5. 最长回文子串

难度：中等
题目描述：

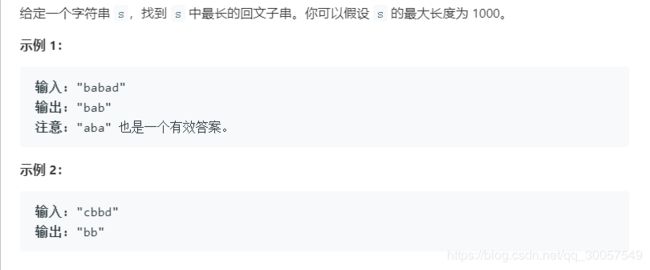
思路总结：一道比较好的动态规划题目。现阶段，重视的是速度，先大致了解下所有的题目类型。如果深挖的话，时间上很有可能来不及。

1. 状态 dp[i][j]——True表示在下标i和j组成的子串是一个回文串
2. 状态转移 dp[i][j] = True (if d[i+1][j-1] =True and s[i] == s[j+1])
3. 初始化 一个字符全为True，两个字符也进行初始化
   题解一：暴力法

class Solution:
    def longestPalindrome(self, s: str) -> str:
        #思路：遍历所有的子串，进行判断 时间复杂度O(n^3)
        def isPali(s):
            pureStr = ''.join(filter(str.isalnum, s))
            return pureStr == pureStr[::-1]
        if len(s) == 0:return ""
        max_ = s[0]
        for l in range(len(s)):
            for r in range(l+1, len(s)):
                if isPali(s[l:r+1]):
                    if len(max_) < r-l+1:
                        max_ = s[l:r+1]
        return max_

题解一结果：
肯定是超时
题解二：动态规划

"""
我的动态规划解法，还尼玛超时
class Solution:
    def longestPalindrome(self, s: str) -> str:
        #思路：动态规划。
        #状态转移方程：dp[i][j] = True (if d[i+1][j-1] =True and s[i] == s[j+1])
        n = len(s)
        if n == 0:return ""
        #初始化了一个字符和两个字符的回文串
        dp = [[True if i==j or (j==i+1 and s[i]==s[i+1]) else False for j in range(n)] for i in range(n)]
        count = 1
        while True:
            if count == 0:break
            count = 0
            for i in range(n):
                for j in range(n):
                    if dp[i][j] == False and i+1 < n and j-1 > 0 and dp[i+1][j-1] and s[i] == s[j]:
                        dp[i][j] = True
                        count += 1
        res = ()
        max_ = 0
        #找出最长子串下标
        for i in range(n):
            for j in range(n):
                if dp[i][j] == True and j-i+1 > max_:
                    max_ = j-i+1
                    res=(i,j)
        return s[res[0]:res[1]+1]
        
"""
class Solution:
    def longestPalindrome(self, s: str) -> str:
        #思路：动态规划。
        #状态转移方程：dp[i][j] = True (if d[i+1][j-1] =True and s[i] == s[j+1])
        n = len(s)
        if n <= 1:return s
        #初始化了一个字符和两个字符的回文串
        dp = [[False for j in range(n)] for i in range(n)]
        # dp[]
        res = s[0]
        for j in range(1,n):
            for i in range(j):
                if (j-i <=2 or dp[i+1][j-1]) and s[i] == s[j]:
                    dp[i][j] = True
                    if j-i+1 >len(res):
                        res = s[i:j+1]
        return res
        

题解二结果：