131.分割回文串&132.分割回文串Ⅱ

131.分割回文串

难度：中等&困难
先看下第一题。
题目描述：

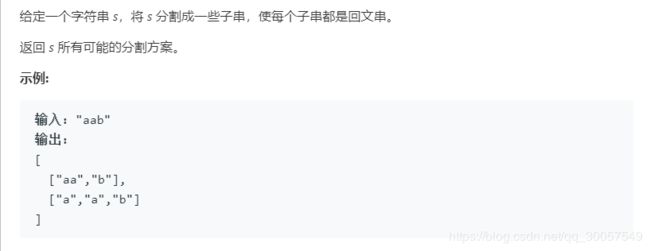
思路总结：分割字符串，初步看一下输入输出，发现输出是对字符串的分割，此时会立马想到分治法（回溯法亦可），采用递归实现。可以视作DFS。
题解一：

class Solution:
    def partition(self, s: str) -> List[List[str]]:
        #思路：自然而然想到暴力法，但是貌似又是超时，然后又想到了双指针，如果子
        #串不是回文串，那么从当前子串开头往后的子串也不是回文串，这种优化的理论
        #复杂度应该是O(n^2),这里“应该”一词预示着需要学习一下时间复杂度相关计
        #算方法了。
        #如果不好返回，就将tmp传进去
        def helper(s,tmp):
            if not s:res.append(tmp)
            for i in range(1,len(s)+1):
                if s[:i] == s[:i][::-1]:
                	#这里的s[:i]需要用[]包起来，因为tmp是list
                    helper(s[i:], tmp+[s[:i]]) 
        res = []
        helper(s,[])
        return res

题解一结果：

132.分割回文串Ⅱ

再看下第二题，这题如果有131的基础，很自然而然的想到将131递归传进去的分割序列换成分割长度，然后找最小。
难度：困难
题目描述：

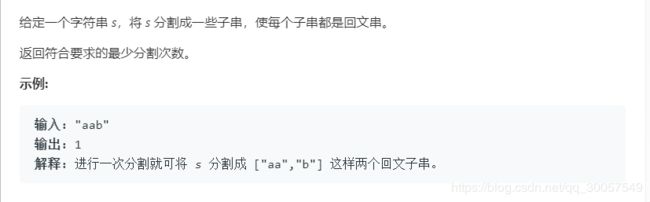
思路总结：有人将此题思路分为自上而下和自下而上，也有人提出分治、回溯等解法。这里我先用一种python自带的缓存函数返回值的工具函数实现一种自顶向下（分治）的解法来占个坑。日后填坑。
题解一：

import functools
class Solution:
    @functools.lru_cache(None)
    def minCut(self, s: str) -> int:
        if s == s[::-1]:return 0
        ans = float("inf")
        for i in range(1, len(s)+1):
            if s[:i] == s[:i][::-1]:
                ans = min(self.minCut(s[i:]) + 1, ans)
        return ans

题解一结果：

分割回文串总结

这两个题可以看做是一个题，只不过后一题在前一题的基础上更容易超时。（函数栈太长）