AcWing 343 排序

题目描述：

给定 n 个变量和 m 个不等式。其中 n 小于等于26，变量分别用前 n 的大写英文字母表示。

不等式之间具有传递性，即若 A>B 且 B>C ，则 A>C。

请从前往后遍历每对关系，每次遍历时判断：

• 如果能够确定全部关系且无矛盾，则结束循环，输出确定的次序；
• 如果发生矛盾，则结束循环，输出有矛盾；
• 如果循环结束时没有发生上述两种情况，则输出无定解。

输入格式

输入包含多组测试数据。

每组测试数据，第一行包含两个整数n和m。

接下来m行，每行包含一个不等式，不等式全部为小于关系。

当输入一行0 0时，表示输入终止。

输出格式

每组数据输出一个占一行的结果。

结果可能为下列三种之一：

1. 如果可以确定两两之间的关系，则输出 "Sorted sequence determined after t relations: yyy...y.",其中't'指迭代次数，'yyy...y'是指升序排列的所有变量。
2. 如果有矛盾，则输出： "Inconsistency found after t relations."，其中't'指迭代次数。
3. 如果没有矛盾，且不能确定两两之间的关系，则输出 "Sorted sequence cannot be determined."。

数据范围

2≤n≤26，变量只可能为大写字母A~Z。

输入样例1：

4 6
A

输出样例1：

Sorted sequence determined after 4 relations: ABCD.
Inconsistency found after 2 relations.
Sorted sequence cannot be determined.

输入样例2：

6 6
A

输出样例2：

Inconsistency found after 6 relations.

输入样例3：

5 5
A

输出样例3：

Sorted sequence determined after 4 relations: ABCDE.

分析：

本题考察Floyd算法在传递闭包问题上的应用。给定若干对元素和若干对二元关系，并且关系具有传递性，通过传递性推导出尽量多的元素之间的关系的问题被称为传递闭包。比如a < b,b < c,就可以推导出a < c，如果用图形表示出这种大小关系，就是a到b有一条有向边，b到c有一条有向边，可以推出a可以到达c，找出图中各点能够到达点的集合，就类似于Floyd算法求图中任意两点间的最短距离。Floyd求解传递闭包问题的代码如下：

void floyd(){
    for(int k = 0;k < n;k++)
        for(int i = 0;i < n;i++)
            for(int j = 0;j < n;j++)
                f[i][j] |= f[i][k] & f[k][j];
}

只是对原来算法在状态转移方程上略加修改 就能够求解传递闭包问题了。f[i][j] = 1表示i可以到达j ( i < j)，f[i][j] = 0表示i不可到达j。只要i能够到达k并且k能够到达j，那么i就能够到达j，这就是上面代码的含义。

对于本题而言，给定n个元素和一堆二元关系，依次读取每个二元关系，在读取第i个二元关系后，如果可以确定n个元素两两间的大小关系了，就输出在几对二元关系后可以确定次序，并且次序是什么；如果出现了矛盾，就是A < B并且B < A这种情况发生了就输出多少对二元关系后开始出现矛盾；如果遍历完所有的二元关系还不能确定所有元素间的大小关系，就输出无法确定。

可以发现，题目描述要求按顺序遍历二元关系，一旦前i个二元关系可以确定次序了就不再遍历了，即使第i + 1对二元关系就会出现矛盾也不去管它了。对于二元关系的处理和之前的做法一样，A < B，就将f[0][1]设为1，题目字母只会在A到Z间，因此可以映射为0到25这26个元素，如果f[0][1] = f[1][0] = 1，就可以推出f[0][0] = 1，此时A < B并且A > B发生矛盾，因此在f[i][i]= 1时发生矛盾。

下面详细分析下求解的步骤：首先每读取一对二元关系，就执行一遍Floyd算法求传递闭包，然后执行check函数判断下此时是否可以终止遍历，如果发生矛盾或者次序全部被确定就终止遍历，否则继续遍历。在确定所有的次序后，需要输出偏序关系，因此需要执行下getorder函数。注意这里的终止遍历仅仅是不再针对新增的二元关系去求传递闭包，循环还是要继续的，需要读完数据才能继续读下一组数据。

下面设计check函数和getorder函数。

int check(){
    for(int i = 0;i < n;i++)
        if(f[i][i]) return 0;
    for(int i = 0;i < n;i++){
        for(int j = 0;j < i;j++){
            if(!f[i][j] && !f[j][i])    return 1;
        }
    }
    return 2;
}

如果f[i][i] = 1就发生矛盾了，可以返回了；如果f[i][j] = f[j][i] = 0表示i与j之间的偏序关系还没有确定下来，就需要继续读取下一对二元关系；如果所有的关系都确定了，就返回2。

string getorder(){
    char s[26];
    for(int i = 0;i < n;i++){
        int cnt = 0;
        for(int j = 0;j < n;j++)    cnt += f[i][j];
        s[n - cnt - 1] = i + 'A';
    }
    return string(s,s + n);
}

确定所有元素次序后如何判断元素i在第几个位置呢？f[i][j] = 1表示i < j，因此计算下下i小于元素的个数cnt，就可以判定i是第cnt + 1大的元素了。

总的代码如下：

#include 
#include 
#include 
#include 
using namespace std;
const int N = 27;
int n,m,g[N][N],f[N][N];
void floyd(){
    memcpy(f,g,sizeof g);
    for(int k = 0;k < n;k++)
        for(int i = 0;i < n;i++)
            for(int j = 0;j < n;j++)
                f[i][j] |= f[i][k] & f[k][j];
}
int check(){
    for(int i = 0;i < n;i++)
        if(f[i][i]) return 0;
    for(int i = 0;i < n;i++){
        for(int j = 0;j < i;j++){
            if(!f[i][j] && !f[j][i])    return 1;
        }
    }
    return 2;
}
string getorder(){
    char s[26];
    for(int i = 0;i < n;i++){
        int cnt = 0;
        for(int j = 0;j < n;j++)    cnt += f[i][j];
        s[n - cnt - 1] = i + 'A';
    }
    return string(s,s + n);
}
int main(){
    while(cin>>n>>m,n || m){
        string str;
        int type = 1;
        memset(g,0,sizeof g);
        for(int i = 1;i <= m;i++){
            cin>>str;
            if(type != 1)   continue;
            int a = str[0] - 'A',b = str[2] - 'A';
            g[a][b] = 1;
            floyd();
            type = check();
            if(!type)   printf("Inconsistency found after %d relations.\n",i);
            else if(type == 2){
                string ans = getorder();
                printf("Sorted sequence determined after %d relations: %s.\n",i,ans.c_str());
            }   
        }
        if(type == 1)   printf("Sorted sequence cannot be determined.\n");
    }
    return 0;
}

 分析上面的代码可以发现，每读取一对二元关系就去执行一次floyd算法，时间复杂度是O(m*n^3)，显然冗余度很高，新增了a与b的大小关系，只需要更改由这条边可传递下去的关系即可，比如之前执行floyd已经确定A < C，新增了B < D，完全没必要再去求解A与C的大小关系了。因此，如果新读入的二元关系f[a][b]已经是1了，表示之前的算法已经使用了a与b这条边了，就不需要再执行传递闭包算法了，如果f[a][b] = 0，也只需要更新与a、b有关点的关系。

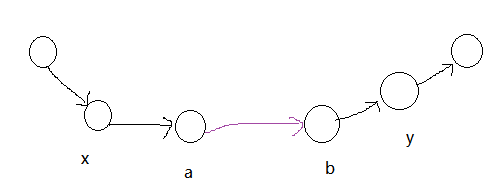
如上图所示，加入a与b这条边后，我们只需要遍历能够到达a的所有点x以及b能够到达所有的点y，用平方级复杂度就可以完成加一条边后关系的更新。f[a][b] = 1，首先我们需要更新f[x][b]与f[a][y]的值为1，表示x可以到达b了，a可以到达y了，最后再更新f[x][y] = 1。注意这里的x与y都是泛指，x指的是能够到达a的点，不一定是图中标的与a直接相连的那个点，也可能是图中x的上一点，也是可以到达a的。这样一来每读入一条边最多只要平方级别复杂度就可以完成更新，总的时间复杂度为O(m*n^2)，效率也大幅提升了。这种方法的代码如下：

#include 
#include 
#include 
#include 
using namespace std;
const int N = 27;
int n,m,f[N][N];
int check(){
    for(int i = 0;i < n;i++)
        if(f[i][i]) return 0;
    for(int i = 0;i < n;i++){
        for(int j = 0;j < i;j++){
            if(!f[i][j] && !f[j][i])    return 1;
        }
    }
    return 2;
}
string getorder(){
    char s[26];
    for(int i = 0;i < n;i++){
        int cnt = 0;
        for(int j = 0;j < n;j++)    cnt += f[i][j];
        s[n - cnt - 1] = i + 'A';
    }
    return string(s,s + n);
}
int main(){
    while(cin>>n>>m,n || m){
        string str;
        int type = 1;
        memset(f,0,sizeof f);
        for(int i = 1;i <= m;i++){
            cin>>str;
            if(type != 1)   continue;
            int a = str[0] - 'A',b = str[2] - 'A';
            if(!f[a][b]){
                f[a][b] = 1;
                for(int x = 0;x < n;x++){
                    if(f[x][a]) f[x][b] = 1;
                    if(f[b][x]) f[a][x] = 1;
                    for(int y = 0;y < n;y++){
                        if(f[x][a] && f[b][y])  f[x][y] = 1;
                    }
                }
            }    
            type = check();
            if(!type)   printf("Inconsistency found after %d relations.\n",i);
            else if(type == 2){
                string ans = getorder();
                printf("Sorted sequence determined after %d relations: %s.\n",i,ans.c_str());
            }   
        }
        if(type == 1)   printf("Sorted sequence cannot be determined.\n");
    }
    return 0;
}