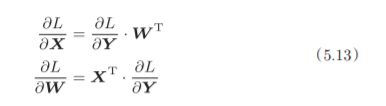神经网络基础学习笔记（四）误差反向传播法

目录

误差反向传播

前言：

5.1 计算

5.1.1　用计算图求解

5.2 链式法则

5.2.1 计算图的反向传播

5.2.2　什么是链式法则

5.3 反向传播

5.3.1　加法节点的反向传播

5.3.2　乘法节点的反向传播

5.3.3　苹果的例子

5.4 简单层的实现

5.4.1　乘法层的实现

5.4.2　加法层的实现​

5.5 激活函数层的实现

5.5.2　Sigmoid层

5.6.2　批版本的Affine层

5.7 误差反向传播法的实现

5.7.1　神经网络学习的全貌图

5.7.2　对应误差反向传播法的神经网络的实现

5.7.3　误差反向传播法的梯度确认

5.7.4　使用误差反向传播法的学习

5.8 小结

---

误差反向传播法

前言：

数值微 分虽然简单，也容易实现，但缺点是计算上比较费时间。本章我们将学习一 个能够高效计算权重参数的梯度的方法——误差反向传播法

正确理解误差反向传播法：一种是基于数学式； 另一种是基于计算图（computational graph）

5.1 计算

5.1.1　用计算图求解

节点用○表示，○中是计算的内容。

也可以表示为:

5.2 链式法则

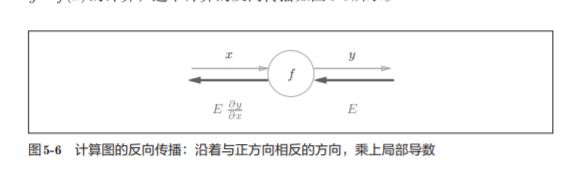
5.2.1 计算图的反向传播

5.2.2　什么是链式法则

以高数里面的复合函数为励志

z = (x + y) ^2

规则：

如果某个函数由复合函数表示，则该复合函数的导数可以用构成复 合函数的各个函数的导数的乘积表示。

5.2.3　链式法则和计算图

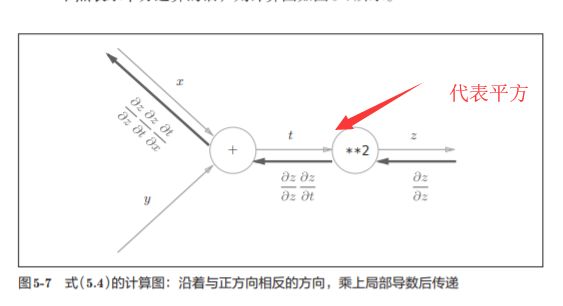
我们尝试将式（5.4）的链式法则的计算用计算图表示出来

有上面的公式运算易得：

5.3  反向传播

上一节介绍了计算图的反向传播是基于链式法则成立的。下面以+ * 等运算未例子

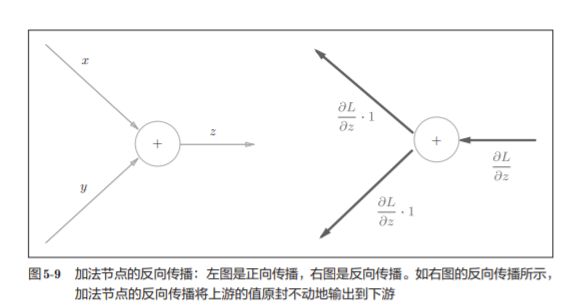
5.3.1　加法节点的反向传播

z = x + y的导数

则得到：

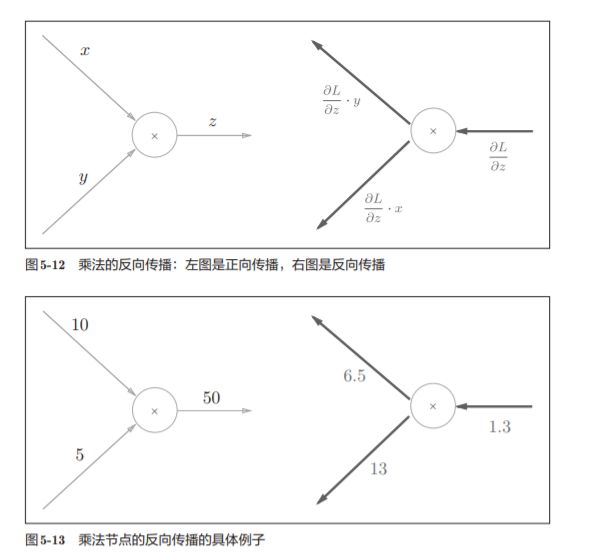
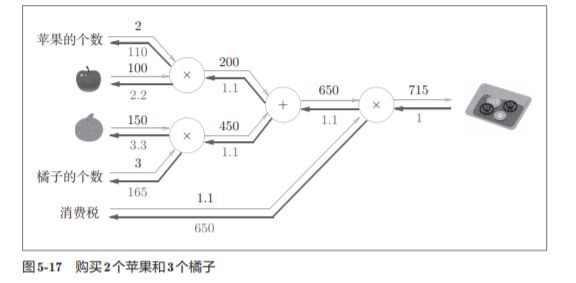
5.3.2　乘法节点的反向传播

“翻转值”---太直观了吧 就是xy求偏导的时候出现的情况

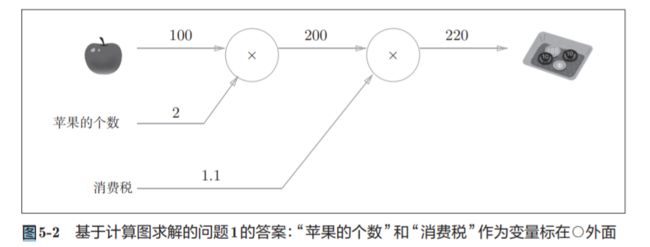
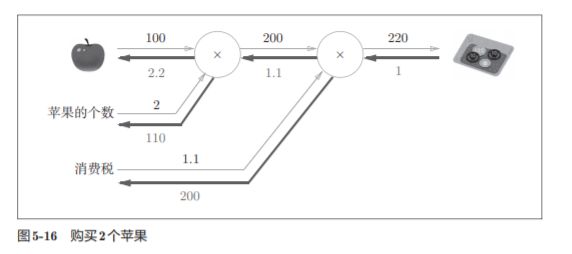
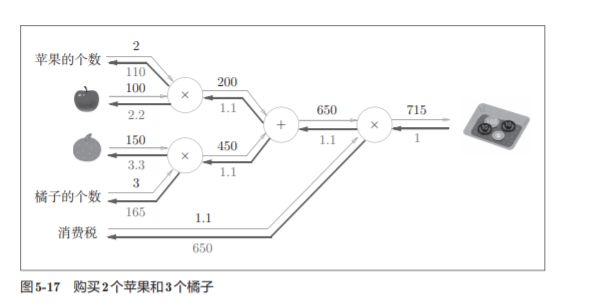
5.3.3　苹果的例子

练习：

答案：

5.4 简单层的实现

乘法节点称为“乘法层”（MulLayer），加法节点称为“加法层”

5.4.1　乘法层的实现

举个栗子：

实现代码：

注意： 每一层  要分开

各个变量的导数可由backward()求出

5.4.2　加法层的实现

加法层的forward()接收x和y两个参数，将它 们相加后输出。

backward()将上游传来的导数（dout）原封不动地传递给下游

实现代码：

5.5 激活函数层的实现

们将计算图的思路应用到神经网络中。

我们把构成神经 网络的层实现为一个类。先来实现激活函数的ReLU层和Sigmoid层

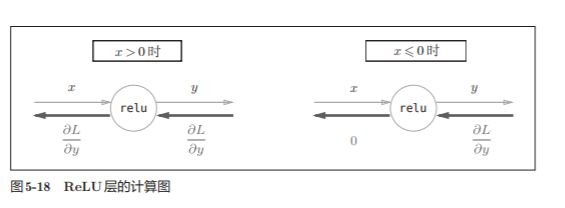
5.5.1　ReLU层

在神经网络的层的实现中，一般假定forward() 和backward()的参数是NumPy数组。

实现代码：

实现代码：

关于（x<=0）的解释

如果正向传播时的输入值小于等于0，则反向传播的值为0。 因此，反向传播中会使用正向传播时保存的mask，将从上游传来的dout的 mask中的元素为True的地方设为

5.5.2　Sigmoid层

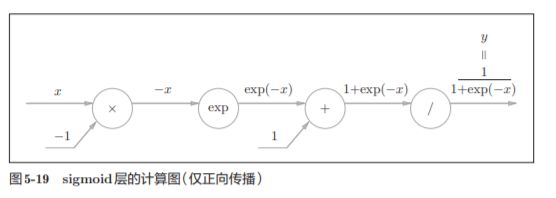
实现sigmoid函数。sigmoid函数由式（5.9）表示

计算图表示式（5.9）的话，则如图5-19所示

出现了新的“exp”和“/”节点，分别进行y = exp(x)，y=1/x

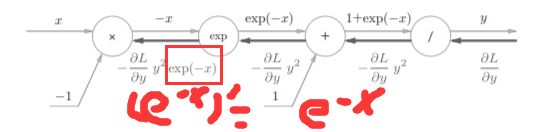
接下来计算他的方向传播

分为四个步骤，上书本的图比较直观

步骤1:

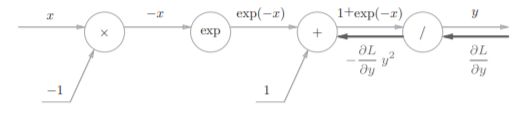
反向传播时，会将上游的值乘以−y 2 （正向传播的输出的 平方乘以−1后的值）后，再传给下游。

步骤2

“+”节点将上游的值原封不动地传给下游。计算图如下所示。

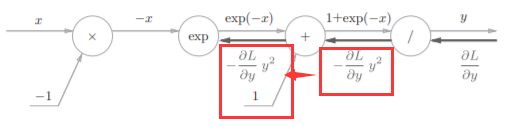
步骤3

步骤4

乘法的话就只需要做一下翻转就可以了

最后我们可以的得到：

因此，我们发现，我们通过正向传播的x和y就可以求出这个公式的数值

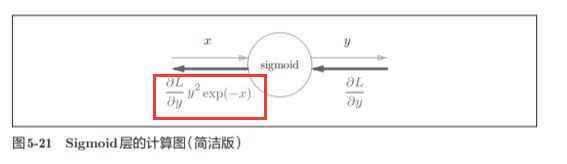
简洁版的计算图可以省略反向传播中的计算过程，因此计算效率更高

，可以不用在意Sigmoid层中琐碎的细节，而只需要 专注它的输入和输出

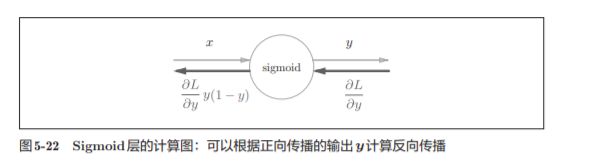
图5-21所表示的Sigmoid层的反向传播，只根据正向传播的输出 就能计算出来

5.6 Affine/Softmax层的实现

神经网络的正向传播中，为了计算加权信号的总和，使用了矩阵的乘 积运算

神经元的加权和可以用Y = np.dot(X, W) + B

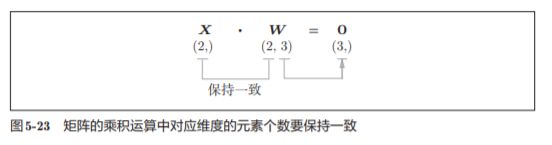
X和W 的乘积必须使对应维度的元素个数一致。

注意这里不是2行矩阵相乘法的意思

神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”A。因此，这里将进行仿射变换的处理实现为“Affine层”。

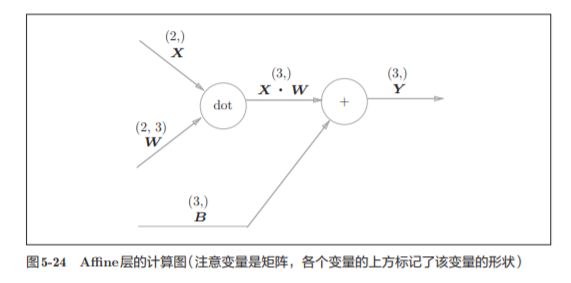
np.dot(X, W) + B的运算可用图5-24 所示的计算图表示出来

之前我们见到的计算图中各个节点间流动的是标量，而这个例子中各个节点 间传播的是矩阵

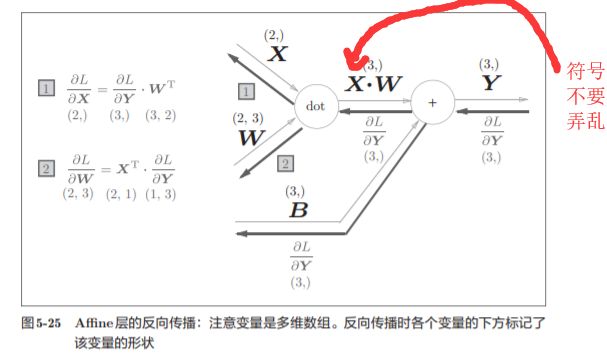
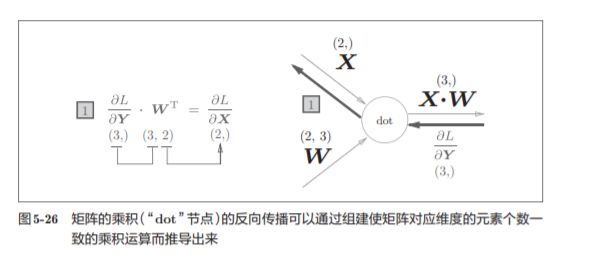
为什么要注意矩阵的形状呢？因为矩阵的乘积运算要求对应维度的元素 个数保持一致，通过确认一致性，就可以导出式（5.13）。

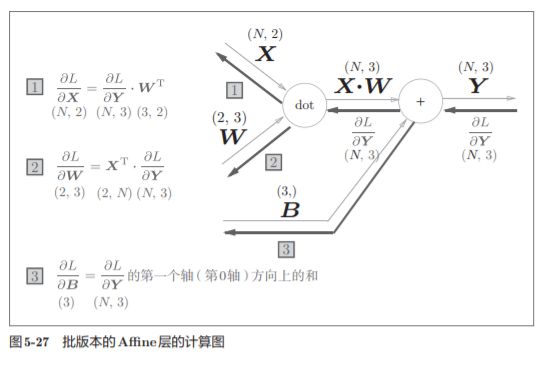
5.6.2　批版本的Affine层

在我们考虑N 个数据一起进行正向传播的情况，也就是批版本的Affi ne层。

与刚刚不同，现在输入X的形状是(N, 2)。之后就和前面一样，在 计算图上进行单纯的矩阵计算。

由于正向传播时，偏置会被加到每一个数据（第1个、第2个……）上。反向传播时，各个数据的反向传播的值需要汇总为偏置的元素。

这个例子中，假定数据有2个（N = 2）。偏置的反向传播会对这2个数据 的导数按元素进行求和

这里使用了np.sum()对第0轴（以数据为单位的轴，axis=0）方向上的元素进行求和

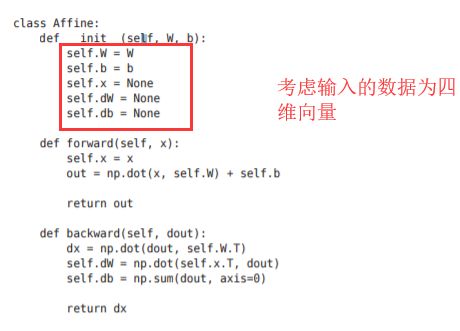
实现考虑了输入数据为张量（四维数据）的情况，与这里介绍的稍有差别

5.6.3　Softmax-with-Loss 层

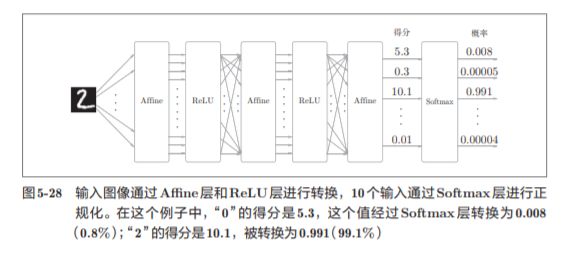
softmax函数，比如手写数字数字识别的时候：

因为手写数字识别要进行10类分类，所以向Softmax层的输 入也有10个。

注意：

神经网络中进行的处理有推理（inference）和学习两个阶段。神经网 络的推理通常不使用 Softmax层。也就是说，当神经网络的推理只需要给出一个答案 的情况下，因为此时只对得分最大值感兴趣，所以不需要 Softmax层。 不过，神经网络的学习阶段则需要 Softmax层。

考虑到这里也包含作为损失函数的交叉熵误 差（cross entropy error），所以称为“Softmax-with-Loss层”。Softmax-withLoss层（Softmax函数和交叉熵误差）的计算图如图5-29所示。

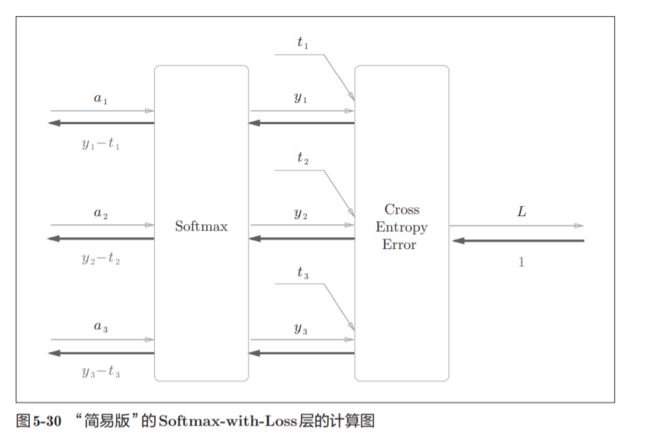
图5-29的计算图可以简化成图5-30

softmax函数记为Softmax层，交叉熵误差记为 Cross Entropy Error层。这里假设要进行3类分类，从前面的层接收3个输 入（得分）。如图5-30所示，Softmax层将输入（a1, a2, a3）正规化，输出（y1, y2, y3）。Cross Entropy Error层接收Softmax的输出（y1, y2, y3）和教师标签（t1, t2, t3），从这些数据中输出损失L。

Softmax层的反向传播得到了 （y1 − t1, y2 − t2, y3 − t3）这样“漂亮”的结果。由于（y1, y2, y3）是Softmax层的 输出，（t1, t2, t3）是监督数据，所以（y1 − t1, y2 − t2, y3 − t3）是Softmax层的输 出和教师标签的差分。

神经网络学习的目的就是通过调整权重参数，使神经网络的输出（Softmax 的输出）接近教师标签。

必须将神经网络的输出与教师标签的误差高 效地传递给前面的层

具体例子：

如思考教师标签是（0, 1, 0），Softmax层 的输出是(0.3, 0.2, 0.5)的情形。因为正确解标签处的概率是0.2（20%），这个 时候的神经网络未能进行正确的识别。此时，Softmax层的反向传播传递的 是(0.3, −0.8, 0.5)这样一个大的误差。因为这个大的误差会向前面的层传播， 所以Softmax层前面的层会从这个大的误差中学习到“大”的内容。

注意：

使用“平 方和误差”作为“恒等函数”的损失函数，反向传播才能得到（y1 − t1, y2 − t2, y3 − t3）这样“漂亮”的结果。

再举一个例子，比如思考教师标签是(0, 1, 0)，Softmax层的输出是(0.01, 0.99, 0)的情形（这个神经网络识别得相当准确）。此时Softmax层的反向传播 传递的是(0.01, −0.01, 0)这样一个小的误差。这个小的误差也会向前面的层 传播，因为误差很小，所以Softmax层前面的层学到的内容也很“小”。

Softmax-with-Loss层的实现

请注意反向传播时，将要传播 的值除以批的大小（batch_size）后，传递给前面的层的是单个数据的误差

5.7 误差反向传播法的实现

5.7.1　神经网络学习的全貌图

神经网络的学习分为下面4个步骤

的误差反向传播法会在步骤2中出现

在上一节的实验，我们采用数值微分的方法进行实现，虽然简单，但是消耗时间过长。

5.7.2　对应误差反向传播法的神经网络的实现

这里我们要把2层神经网络实现为TwoLayerNet

与上一章非常类似

不同点主要在于这里使用了层。通过使用层，获得识别结果 的处理（predict()）和计算梯度的处理（gradient()）只需通过层之间的传递就能完成。

只截取不同的部分:

请注意这个实现中的粗体字代码部分，尤其是将神经网络的层保存为 OrderedDict这一点非常重要。OrderedDict是有序字典，“有序”是指它可以 记住向字典里添加元素的顺序。神经网络的正向传播只需按照添加元 素的顺序调用各层的forward()方法就可以完成处理，而反向传播只需要按 照相反的顺序调用各层即可。

因为Affine层和ReLU层的内部会正确处理正 向传播和反向传播，所以这里要做的事情仅仅是以正确的顺序连接各层，再 按顺序（或者逆序）调用各层

只需像组装乐高 积木那样添加必要的层就可构件一个较大的神经网络。

5.7.3　误差反向传播法的梯度确认

两种求梯度的方法：

一种是基于数值微分的方 法，另一种是解析性地求解数学式的方法。后一种方法通过使用误差反向传 播法，即使存在大量的参数，也可以高效地计算梯度。使用误差反向传播法求梯度。

在确认误差反向传播法的实现是否正确时，是需要用到数值微分的。

确认数值 微分求出的梯度结果和误差反向传播法求出的结果是否一致（严格地讲，是 非常相近）的操作称为梯度确认（gradient check）。

这里误差的计 算方法是求各个权重参数中对应元素的差的绝对值，并计算其平均值。运行 上面的代码后，会输出如下结果

比如，第1层的偏置的误差是9.7e-13（0.00000000000097）。这样一来， 我们就知道了通过误差反向传播法求出的梯度是正确的，误差反向传播法的 实现没有错误。

5.7.4　使用误差反向传播法的学习

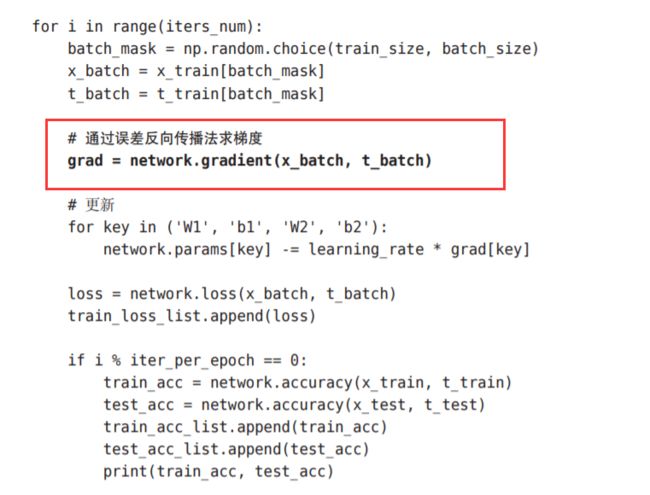
我们来看一下使用了误差反向传播法的神经网络的学习的实现。 和之前的实现相比，不同之处仅在于通过误差反向传播法求梯度这一点。

使用部分，与上一张的不同点只在于：

5.8 小结

使用计算图，介绍了神 经网络中的误差反向传播法，并以层为单位实现了神经网络中的处理，我们 学过的层有ReLU层、Softmax-with-Loss层、Affine层、Softmax层等，这 些层中实现了forward和backward方法，通过将数据正向和反向地传播，可 以高效地计算权重参数的梯度。通过使用层进行模块化，神经网络中可以自 由地组装层，轻松构建出自己喜欢的网络。