模拟IC设计——sigma delta ADC原理分析

一. ADC原理

对于 Nyquist 和 Shannon 定理的检验将证明：ADC 采样频率的选择与最大输入信号频率对输入信号带宽的比率有很强的相关性。

1. Nyquist准则（欠采样准则）

如果要从相等时间间隔取得的采样点中，毫无失真地重建模拟信号波形，则采样频率必须大于或等于模拟信号中最高频率成份的两倍。因而对于一个最大信号频率为 fMAX的模拟信号 fa，其最小采样频率 fs，则有 fs ≥ 2 * fMAX

Nyquist频率：采样频率的一半，即 fs/2。从理论上来讲奈奎斯特频率正好大于输入信号的最大频率。

2. Shannon定理

一个带宽为fb的模拟信号，采样速率必须为 fs > 2fb，才能避免信息的损失。信号带宽可以从 DC 到 fb（基带采样），或从 f1 到f2，其中 fb = f2-f1(欠采样)。

3. 信号混叠

具体参见链接：https://zhuanlan.zhihu.com/p/23923059

如果不满足采样定理条件，采样后的信号的频率就会重叠。即被采样信号中高于采样频率一半（fs/2）的那部分频率成分将被重建成低于fs/2信号。这种频谱的重叠导致的失真称为混叠。（可借助车轮效应理解）

（1）出现原因：
若采样频率小于2倍的信号频率，即 fs < 2 * fa，那么，采样后的信号将存在混叠。
理论上，如果信号中没有高于奈奎斯特频率的频率成分，那么则不存在混叠。

（2）解决办法：
a.提高采样频率 fs，一般实际应用中保证 fs 为 fMAX 的2.56~4倍。
b.加一个低通滤波器：抗混叠滤波器
   理想状态下，该滤波器可使低于奈奎斯特频率的频率通过，移除高于奈奎斯特频率的频率成分

4. 性能指标

1 静态指标

a.积分非线性（INL）：输入一输出特性曲线与连接两端点的直线之间的最大偏差
b.微分非线性（DNL）：在输入轴上两个连续码转换点之间的差值与理想 1LSB 值的最大偏差
c.失调：直线AB通过端点的垂直截距
d.增益误差：直线AB的斜率与理想值1之间的偏差

2 动态指标

a.信号与噪声失真比（SNDR）:是当输入为正弦时，输出端信号功率与总噪声及谐波功率的比。
b.动态范围：满量程正弦输入功率与肼限=0 dB时的正弦输入功率的比值
c.总谐波失真：所有谐波能量（除去基波）之和除以基频的能量

二. Σ-Δ 原理

0.常用单级分类

1 根据modulator是否使用开关电容电路分

a.连续时间模式（无开关电容）：
优点：功耗更小，无开关电容对时钟噪声不敏感，调制速度更快，常用于转换较高频率信号。
缺点：要通过RC值来确定的积分系数，而不是像离散时间模式是用电容比值来确定的；对反馈回来的脉冲波形比较敏感，它会影响输入信号。
b.离散时间模式则（有开关电容）
与前者相反。

2 根据modulator阶数分

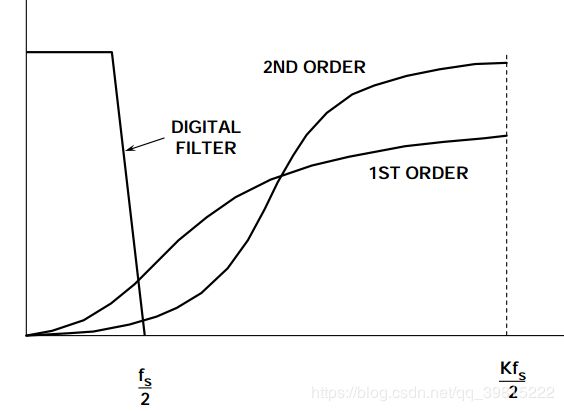
所谓阶数指的是sigma—Delta调制器中积分器的个数。一般阶数越高幅频特性越好，低频段的衰减也越厉害，高频段的通过性越好所能达到的有效位数越大，但是延迟也会很大，也会减小输入信号的摆幅，另外，由于噪声在高频的幅值过大，会使整个系统的稳定性降低。

3 根据量化器的位数分

可以分为一位调制器和多位调制器。使用多位量化器可以增加SNR，使系统容易稳定，产生较少的谐波分量，使降采样滤波器变得相对简单；但是多位量化器增加了ADC的复杂性，并且要求用于反馈的多位DAC有足够的精度来保证最后量化的精度。
 

1.基本原理

（图片来源于ANALOG DEVICES)  
1 过采样

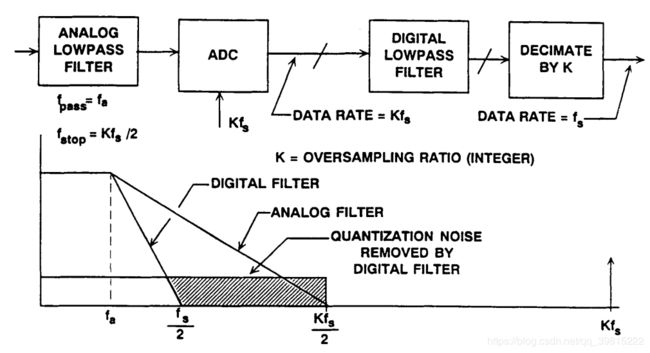
指以高于信号带宽2倍或其最高频率对其采样的过程。K即为过采样率（OSR）。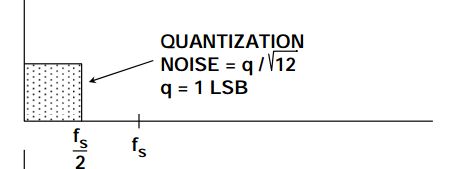

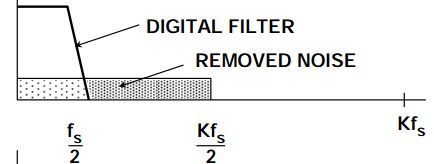
目的：a. 由于采用 Kfs 采样频率，均方根值为 q/√12 的量化噪声分布在 DC 到 Kfs/2 的带宽范围内，降低了某一频率下的噪声幅值，从而提高了信噪比，根据信噪比（SNR）和实际分辨率（ENOB）公式：
                    ENOB=(SNR-1.76)/6.02             （SNR=6.02*N+1.76）
          可见提高了实际分辨率
          b.同时减轻了模拟抗混叠滤波器的要求

2 量化噪声整形

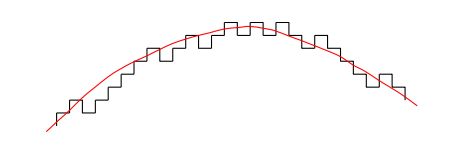（采样频率和量化值之间的关系，红线是实际电压值）
离散化的阶梯型与红色的模拟信号相减的值即为量化噪声。实际上，阶梯型线条包围的面积和模拟信号包围的面积是相等的，即二者能量总量是相等的。量化噪声是消除不了的。
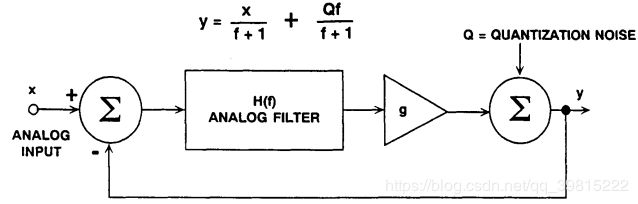
根据频域线性模型y和x的关系，f越大，Q引起的噪声就越大，即类似高通滤波器（x部分则是低通滤波器）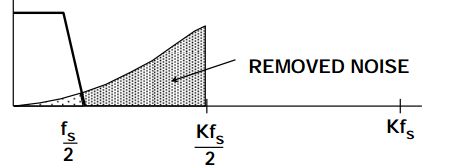

3 数字抽取滤波

通过数字滤波器将比较器输出的高频一位或多位量化值转换为频率较低的多位量化值。
可理解为降采样滤波器可将n个输入信号加起来，然后除以n，这样获得输入的平均值。
优点：当采样频率下降n倍时，fs/n及其谐波分量处的噪声被混叠到信号带内，其引入的噪声会比较小。

4 数据流的计算

该部分举例分析：
若调制器DAC的参考电压Vref为1V，现输入模拟电压值0.5V，则调制器输出为011101110111的序列，如图所示：3/4代表调制器分辨率为2，6/8代表分辨率为3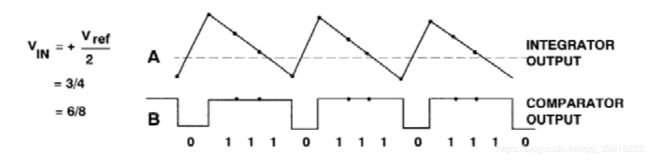

则实际电压Vin=(3/4-2/4)*(1-(-1))=0.5V, 即Vin=(weight(1)-1/2)*Vref*2

5 频域线性模型

输出值y和输入值x，以及量化噪声Q，信号频率f之间的关系

2.ADC组成

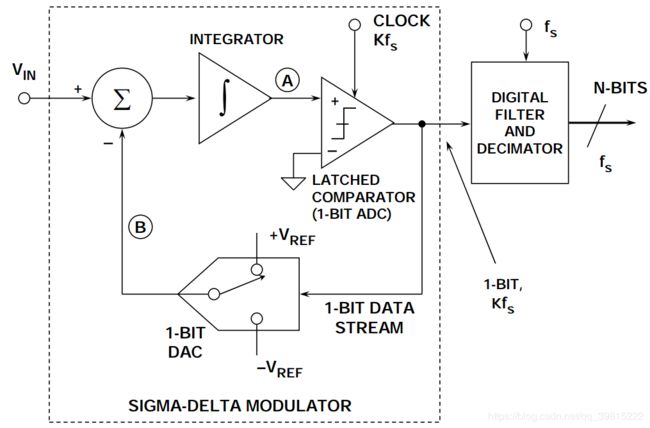（图片来源于ANALOG DEVICES)  
（1）模拟部分：
         a.模拟抗混叠滤波器，
         b.ADC部分：一个比较器、一个基准电压源、一个开关以及一个或多个的积分器与模拟求和电路
（2）数字部分：
         一个DSP（通常但不总是低通滤波器使用）

三.设计流程

1.数字抽取滤波器设计

在设计数字滤波器时，滤波器的采样频率就是前端AD的采样频率。

不同阶数的CIC滤波器的延迟问题：
       当数字滤波器处理来自Σ-Δ调制器的数据流的移动平均值时，存在一个相关的建立时间。该延迟对所有FIR滤波器是固定的，但对不同阶数的CIS滤波器，该延迟是不同的。通常用两项来描述该延迟：群延迟和建立时间。群延迟描述从输入端存在模拟信号到在数字输出端看到它的延迟时间。例如对于单音正弦波，群延迟就是从模拟输入端存在该正弦波电压峰值到该峰值出现在数字输出端的时间差。
       建立时间是指数字滤波器的全部均值时间。如果模拟输入端有一个阶跃，那么需要经过滤波器的完全建立时间， ADC的数据输出才与阶跃之前的输入无关。还可能存在其他延迟，如滤波器的计算时间等。

       本次设计的数字抽取滤波器为3阶的CIC滤波器，与一般的FIR滤波器相比，后者则需要大量的乘法器，而前者只需要加法器和延时，简化了运算，适合用于抽取前级和内插后级等告诉场合，但是也有明显不足：幅频特性无法像 FIR 那样灵活设计，因而有时在抽取的后级会用 FIR 来整形。因此该设计主要由级联积分梳状(CIC)抽取滤波器、CIC补偿滤波器和半带(HB)滤波器组成。
       cIc抽取滤波器作为数字抽取滤波器的第一级来达到降速作用；
       CIC补偿滤波器用来补偿通带的衰减；
       HB滤波器则用作抽取滤波器的阻带衰减及进一步降低采样频率。

用FDAtool设计CIC decimator时，通带增益不是0dB，需要级联一个常数增益滤波器，CIC滤波器增益为D^Q，D是抽取因子，Q是级数，常数增益滤波器增益设置为1/（D^Q），就行，在脚本中输入  G=dfilt.scalar，G.Gain=1/(D^Q)；然后从工作区引入滤波器，设置完参数和CIC级联。