树状数组与前缀和差分数组以及二维树状数组
树状数组与前缀和差分数组以及二维树状数组
- 树状数组
- 基本思想
- 树状数组实现
- 初始化
- 差分数组与前缀和数组
- 成段修改单点查询
- 成段修改成段查询
- 二维树状数组
- 单点修改成段求和
- 成段修改单点查询
- 成段修改成段求和
- 树状数组的其他应用
- 逆序对
- 二维平面排序
树状数组
基本思想
树状数组有称作Binary Index Tree,顾名思义,就是一种以二进制为索引的数据结构。令源数组记作 A A A,现在考虑求取源数组的前缀和。例如求 Σ i = 1 11 A i \Sigma_{i=1}^{11}{A_{i}} Σi=111Ai。将 11 11 11分解为二进制,有 11 = 8 + 2 + 1 11=8+2+1 11=8+2+1。因此,源数组中11个元素之和转化为了树状数组中3个元素之和。即:
∑ i = 1 11 A i = C 11 + C 10 + C 8 \sum_{i=1}^{11}{A_{i}}=C_{11}+C_{10}+C_8 i=1∑11Ai=C11+C10+C8
当然这个式子之所以成立是因为 C C C数组中的元素实际上是对应的源数组元素之和。如下图所示:
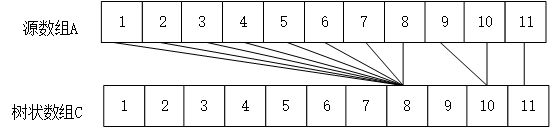
实际上有:
C 11 = A 11 C 10 = A 10 + A 9 C 8 = Σ i = 1 8 A i C_{11}=A_{11} \\ C_{10}=A_{10}+A_9\\C_{8}= \Sigma_{i=1}^{8}{A_{i}} C11=A11C10=A10+A9C8=Σi=18Ai
因此合适安排 C C C数组的内容,即可以在 l o g log log时间内求取前缀和。因为任何数的二进制表示中1的数量都是 l o g log log的。当然,如果仅仅只是静态求和,并不需要树状数组,但是树状数组还可以支持 l o g log log时间的修改操作。
树状数组实现
从实现上说,每个 C i C_i Ci都是从 A i A_i Ai往前累加一定的数量,例如:
C 1 = A 1 C 2 = A 2 + A 1 C 3 = A 3 C 4 = A 4 + A 3 + A 2 + A 1 C 5 = A 5 C 6 = A 6 + A 5 ⋯ C_1=A_1\\C_2=A_2+A_1\\C_3=A_3\\C_4=A_4+A_3+A_2+A_1\\C_5=A_5\\C_6=A_6+A_5\\\cdots C1=A1C2=A2+A1C3=A3C4=A4+A3+A2+A1C5=A5C6=A6+A5⋯
如何确定数量呢?就是 i i i的二进制表示的最低位1所代表的数量。例如:10的二进制表示为1010,所以 C 10 C_{10} C10是两个数相加;5的二进制表示为101,所以 C 5 C_5 C5是一个数相加……这个数量非常容易得到,一般称之为 l o w b i t lowbit lowbit函数,有两个版本,本质上是一样的,如下:
inline int lowbit(int n){return n & (-n);}
inline int lowbit(int n){return n & ( n ^ (n-1) );}
这里面牵涉到补码与位运算,可以具体推导一下。
查询的原理直接如上所示,其代码也非常简单:
//查询源数组[1, x]的区间和
int query(int x){
int sum = 0;
for(;x;x-=lowbit(x)) sum += C[x];
return sum;
}
修改的话,需要考虑每当修改了一个 A i A_i Ai,有哪些包含了该元素的 C j C_j Cj需要修改。结论也很简单:
//将源数组x位置上的数增加delta,源数组索引范围1~N
void modify(int x,int delta){
for(;x<=N;x+=lowbit(x))C[x] += delta;
}
从这里可以看出,树状数组支持单点修改成段求和操作,均可在 l o g log log时间内完成。
初始化
树状数组一个很有意思的点是初始化。假设源数组与树状数组初始均为零,则树状数组就是通过依次调用 m o d i f y ( i , A i ) modify(i, A_i) modify(i,Ai)来实现的。
同时,其实不需要专门保存源数组,因为所有源数组的操作与查询全部都映射到了树状数组上,即所有需要用到的信息树状数组都有保存,无需额外再保存源数组。在很多数据结构中都是这样的情况,源数据结构其实不用保存。
差分数组与前缀和数组
成段修改单点查询
考虑源数组A,令前缀和数组为S,有 S i = Σ A i S_i=\Sigma{A_i} Si=ΣAi。反过来称A是S的差分数组。即,如果令A为源数组,则其差分数组D为:
D 1 = A 1 D i = A i − A i − 1 D_1=A_1\\D_i=A_i-A_{i-1} D1=A1Di=Ai−Ai−1
此时,如果给源数组进行成段修改操作,则相当于差分数组中的两个单点操作。如下:
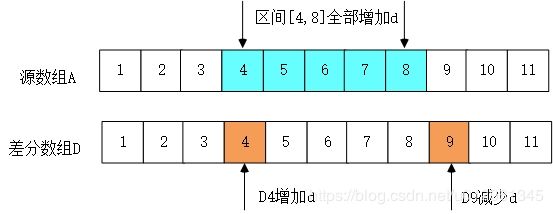
因此,如果针对差分数组D建立一个树状数组,就可以在 l o g log log时间内完成D上的单点操作,也就相当于可以在 l o g log log时间内完成源数组的成段修改操作。不过因为此时树状数组求的是差分数组的前缀和,实际上就是A中某个元素的值,所以,此时树状数组支持的是成段修改、单点查询。
因此可以发现,树状数组要么支持单点修改、成段查询,要么支持成段修改、单点查询。能不能够两个操作都成段呢?
成段修改成段查询
令源数组为A,差分数组为D,则:
∑ i = 1 n A i = D 1 + ( D 1 + D 2 ) + ( D 1 + D 2 + D 3 ) + ⋯ + ( D 1 + ⋯ + D n ) = n ⋅ ∑ i = 1 n D i − ∑ i = 1 n ( i − 1 ) ⋅ D i \sum_{i=1}^{n}A_i=D_1+(D_1+D_2)+(D_1+D_2+D_3)+\cdots+(D_1+\cdots+D_n)\\=n\cdot{\sum_{i=1}^{n}D_i}-\sum_{i=1}^{n}(i-1)\cdot{D_i} i=1∑nAi=D1+(D1+D2)+(D1+D2+D3)+⋯+(D1+⋯+Dn)=n⋅i=1∑nDi−i=1∑n(i−1)⋅Di
这个式子实际上是由两个前缀和构成的,因此可以建立两个树状数组,一个用来操作差分数组,另一个用来操作 ( i − 1 ) ⋅ D i (i-1)\cdot{D_i} (i−1)⋅Di数组。
因此使用2个树状数组即可完成对源数组的成段修改、成段求和操作。
POJ3468,很直白的题目,成段修改,成段求和:
/*
成段修改,区间求和
*/
#include 二维树状数组
单点修改成段求和
在一维基础上,二维树状数组非常好理解且容易实现。只需分别按照行列坐标相加即可。例如:
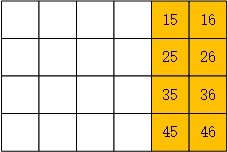
C 46 = ( A 46 + A 45 ) + ( A 36 + A 35 ) + ( A 26 + A 25 ) + ( A 16 + A 15 ) C_{46}=(A_{46}+A_{45})+(A_{36}+A_{35})+(A_{26}+A_{25})+(A_{16}+A_{15}) C46=(A46+A45)+(A36+A35)+(A26+A25)+(A16+A15)
因此二维数组数组可以解决子矩阵和的问题。
//查询源数组[(1,1),(r,c)]的子矩阵和
int query(int r, int c){
int sum = 0;
for(;r;r-=lowbit(r))for(int j=c;j;j-=lowbit(j))sum += C[r][j];
return sum;
}
对于单点修改,也是类似的。
//将源矩阵(r,c)位置上的数增加delta,矩阵为N行M列,从1开始索引
void modify(int r, int c, int delta){
for(;r<=N;r+=lowbit(r))for(int j=c;j<=M;j+=lowbit(j))C[r][j] += delta;
}
成段修改单点查询
与一维情况类似,使用差分可以使得树状数组支持单点查询、成段修改操作。考虑源数组A和差分数组D,令: D 11 = A 11 D i j = A i j + A i − 1 , j − 1 − A i − 1 , j − A i , j − 1 D_{11}=A_{11}\\D_{ij}=A_{ij}+A_{i-1,j-1}-A_{i-1,j}-A_{i,j-1} D11=A11Dij=Aij+Ai−1,j−1−Ai−1,j−Ai,j−1
反过来有: A i j = ∑ u = 1 , v = 1 i , j D u , v A_{ij}=\sum_{u=1,v=1}^{i,j}D_{u,v} Aij=u=1,v=1∑i,jDu,v
即A是D的前缀和数组。
同样的,源数组上的单点查询会变为差分数组上的求和操作;而源数组上的成段修改操作,会变为差分数组上的4个单点操作。对差分数组建立树状数组即可支持相应的操作。
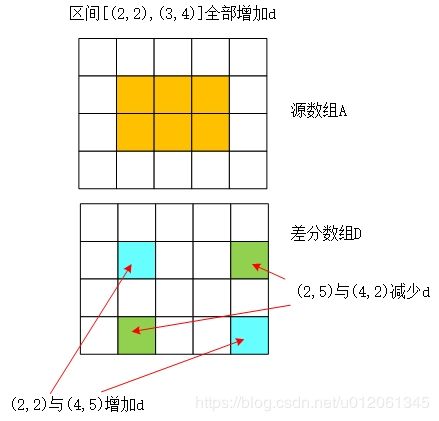
POJ2155在二维数组上要求支持成段修改、单点查询,正好使用差分数组实现。而且该数组是01的,只需做异或和即可。
/*
N×N的矩阵,2种操作
C x1 y1 x2 y2:子矩阵内的所有元素改变状态
Q r y:问(r,y)位置上的元素值
*/
#include 成段修改成段求和
与一维情况类似,考虑源数组中成段求和的情况,变成了差分数组的四重求和:
∑ i , j A i , j = ∑ i = 1 r ∑ j = 1 c ∑ u = 1 i ∑ v = 1 j D u , v \sum_{i,j}A_{i,j}=\sum_{i=1}^{r}\sum_{j=1}^{c}\sum_{u=1}^{i}\sum_{v=1}^{j}D_{u,v} i,j∑Ai,j=i=1∑rj=1∑cu=1∑iv=1∑jDu,v
统计以后可以发现,对每一个 D u , v D_{u,v} Du,v在和式中一共出现了 ( r − u + 1 ) ⋅ ( c − v + 1 ) (r-u+1)\cdot{(c-v+1)} (r−u+1)⋅(c−v+1)次。例如 D 1 , 1 D_{1,1} D1,1出现了 r × c r\times{c} r×c次,而 D r , c D_{r,c} Dr,c出现了1次。所以原式可以写成:
r ⋅ c ⋅ ∑ i = 1 r ∑ j = 1 c D i , j + ∑ i = 1 r ∑ j = 1 c D i , j ⋅ ( i − 1 ) ⋅ ( j − 1 ) − c ⋅ ∑ i = 1 r ∑ j = 1 c D i , j ⋅ ( i − 1 ) − r ⋅ ∑ i = 1 r ∑ j = 1 c D i , j ⋅ ( j − 1 ) r\cdot{c}\cdot\sum_{i=1}^{r}\sum_{j=1}^{c}D_{i,j}+\sum_{i=1}^{r}\sum_{j=1}^{c}D_{i,j}\cdot{(i-1)}\cdot{(j-1)}-c\cdot\sum_{i=1}^{r}\sum_{j=1}^{c}D_{i,j}\cdot{(i-1)}-r\cdot\sum_{i=1}^{r}\sum_{j=1}^{c}D_{i,j}\cdot{(j-1)} r⋅c⋅i=1∑rj=1∑cDi,j+i=1∑rj=1∑cDi,j⋅(i−1)⋅(j−1)−c⋅i=1∑rj=1∑cDi,j⋅(i−1)−r⋅i=1∑rj=1∑cDi,j⋅(j−1)
于是,可以使用4个二维树状数组来实现这个求和操作。因此可以使用4个树状数组来支持源数组的成段修改、成段求和操作。
洛谷4514是一个非常直白的成段修改成段求和的题目。
/*
N×M的矩阵,2种操作成段修改成段更新
Luogu提交要开启O2优化
*/
#include 树状数组的其他应用
树状数组与线段树等不但可以用来求和,还可以用来进行某种情况的计数。只需要改变i与Ai的含义即可。如果源数据中有一个数是a,则树状数组对应的源数组的位置a上加1。这样,查询树状数组所得到的和其实就是满足某些条件的值的数量。相当情况下,这样的处理需要使用到离散化。
逆序对
逆序对问题可以使用经典的分支策略实现,也就是归并排序的一个流程。设原始数据序列为 D D D,令数组A记录: A i A_i Ai表示D中值为i的元素的数量。则对D从后往前,对每一个 D i D_i Di,查询数组A中 [ 1 , D i − 1 ] [1,D_i-1] [1,Di−1]中的和,即可得到D中以 D i D_i Di为首的逆序对数量。
洛谷1908是一个基本的逆序对问题,如果用树状数组或者线段树,需要离散化。
/*
逆序对
*/
#include 二维平面排序
考虑这样一个问题:给定平面点集,对每一个点,问其左下(即x、y坐标均小于)有多少个点。将点集按任一坐标例如按x升序(x相等则按y升序)排序。令数组A记录: A i A_i Ai表示y坐标为i的点的数量。然后遍历点集,对每一个点 P i P_i Pi,查询数组A中 [ 1 , P i . y − 1 ] [1,P_i.y-1] [1,Pi.y−1]的和,即可知道答案。同理也可以求出左上、右下、右上等各方的点的数量。当然,对于严格与不严格的情况,处理上有一定的不同,不过并不复杂。
POJ2481给定区间,要求对每一个区间求出其真父集,相当于求左上点。
/**
给定N个区间[s,e]。
如果a区间能够真包含b区间,则称a比b强壮。
对每一个区间,问比其强壮的区间有多少个
*/
#include