Java篇 - 进制与位运算应用实例

为什么要写这章呢？

阅读过JDK源代码的同学都知道，JDK里充斥着大量的位运算，位运算比一般的运算操作符在效率上快很多，而位运算与进制有着紧密的联系。使用位运算不仅能提高运算效率，还能实现一些奇yin巧技。

看看JDK里的一些位运算的代码：

// java.util.Arrays

public static void parallelSort(char[] a) {
        int n = a.length, p, g;
        if (n <= MIN_ARRAY_SORT_GRAN ||
            (p = ForkJoinPool.getCommonPoolParallelism()) == 1)
            DualPivotQuicksort.sort(a, 0, n - 1, null, 0, 0);
        else
            new ArraysParallelSortHelpers.FJChar.Sorter
                (null, a, new char[n], 0, n, 0,
                 ((g = n / (p << 2)) <= MIN_ARRAY_SORT_GRAN) ?
                 MIN_ARRAY_SORT_GRAN : g).invoke();
    }

// java.math.BigInteger

private static int[] multiplyToLen(int[] x, int xlen, int[] y, int ylen, int[] z) {
        int xstart = xlen - 1;
        int ystart = ylen - 1;

        if (z == null || z.length < (xlen+ ylen))
            z = new int[xlen+ylen];

        long carry = 0;
        for (int j=ystart, k=ystart+1+xstart; j >= 0; j--, k--) {
            long product = (y[j] & LONG_MASK) *
                           (x[xstart] & LONG_MASK) + carry;
            z[k] = (int)product;
            carry = product >>> 32;
        }
        z[xstart] = (int)carry;

        for (int i = xstart-1; i >= 0; i--) {
            carry = 0;
            for (int j=ystart, k=ystart+1+i; j >= 0; j--, k--) {
                long product = (y[j] & LONG_MASK) *
                               (x[i] & LONG_MASK) +
                               (z[k] & LONG_MASK) + carry;
                z[k] = (int)product;
                carry = product >>> 32;
            }
            z[i] = (int)carry;
        }
        return z;
    }

// java.util.Collections的二分查找

private static 
    int indexedBinarySearch(List> list, T key) {
        int low = 0;
        int high = list.size()-1;

        while (low <= high) {
            int mid = (low + high) >>> 1;
            Comparable midVal = list.get(mid);
            int cmp = midVal.compareTo(key);

            if (cmp < 0)
                low = mid + 1;
            else if (cmp > 0)
                high = mid - 1;
            else
                return mid; // key found
        }
        return -(low + 1);  // key not found
    }

进入主题，我们先来看看进制的概念以及进制的分类，转换。

 

1. 进制。

计算机中我们经常使用的进制主要有：二进制、八进制、十进制、十六进制。

二进制，逢二进一，用两个阿拉伯数字：0、1；  

八进制，逢八进一，用八个阿拉伯数字：0、1、2、3、4、5、6、7；

十进制，逢十进一，用十个阿拉伯数字：0到9；  

十六进制，逢十六进一，但我们只有0~9这十个数字，所以用A，B，C，D，E，F这五个字母来分别表示10，11，12，13，14，15，字母不区分大小写。

计算机使用二进制存储数据，为什么不使用八进制、十进制、十六进制？

1.易于物理实现：二进制采用两种物理状态，而十进制是10种，显然前者简单。

2.二进制仅有3种运算规则（可以记成或，且，非），十进制多达55种。

3.机器可靠性高：两种状态较分明。

4.通用性强：与真与假相对应。

5.二进制最简单，只有0和1，计算速度是最快的。

既然二进制优势这么明显，为什么还会存在八进制、十进制、十六进制？

简单来说，就是为了阅读方便。二进制数书写冗长、易错、难记，而十进制数与二进制数之间的转换过程复杂，所以一般用十六进制数或八进制数作为二进制数的缩写。

 

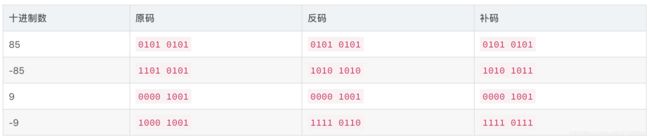
2. 原码 反码 补码。

数值在计算机中是以补码的方式存储的，在探求为何计算机要使用补码之前， 让我们先了解原码， 反码和补码的概念。对于一个数， 计算机要使用一定的编码方式进行存储。 原码， 反码， 补码是计算机存储一个具体数字的编码方式。

一个数在计算机中的二进制表示形式，叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号，正数为0， 负数为1。比如，十进制中的数+2 ，计算机字长为8位，转换成二进制就是[00000010]。如果是 -2 ，就是 [10000010] 。因为第一位是符号位，所以机器数的形式值就不等于真正的数值。例如上面的有符号数 [10000010]，其最高位1代表负，其真正数值是 -2 而不是形式值130（[10000010]转换成十进制等于130）。所以将带符号位的机器数对应的真正数值称为机器数的真值。

原码就是符号位加上真值的绝对值， 即用第一位表示符号， 其余位表示值。
反码的表示方法是: 正数的反码是其本身；负数的反码是在其原码的基础上，符号位不变，其余各个位取反。
补码的表示方法是: 正数的补码就是其本身；负数的补码是在其原码的基础上，符号位不变，其余各位取反，最后+1。 (即在反码的基础上+1)。

举例：

那么计算机为什么要使用补码呢？

首先，根据运算法则减去一个正数等于加上一个负数， 即: 1-1 = 1+(-1)， 所以计算机被设计成只有加法而没有减法，而让计算机辨别”符号位”会让计算机的基础电路设计变得十分复杂，于是就让符号位也参与运算，从而产生了反码。 

用反码计算，出现了”0”这个特殊的数值，0带符号是没有任何意义的。而且会有[0000 0000]和[1000 0000]两个编码表示0。于是设计了补码，负数的补码就是反码+1，正数的补码就是正数本身，从而解决了0的符号以及两个编码的问题: 用[0000 0000]表示0，用[1000 0000]表示-128。 
注意-128实际上是使用以前的-0的补码来表示的，所以-128并没有原码和反码。使用补码，不仅仅修复了0的符号以及存在两个编码的问题， 而且还能够多表示一个最低数。这就是为什么8位二进制，使用补码表示的范围为[-128， 127]。

 

3. 进制转换。

JDK给我们提供了很多显示的进制转换函数：

int n1 = 14;

// 十进制转成十六进制
Integer.toHexString(n1);

// 十进制转成八进制
Integer.toOctalString(n1);

// 十进制转成二进制
Integer.toBinaryString(12);

// 十六进制转成十进制
Integer.valueOf("FFFF",16).toString();

// 十六进制转成二进制
Integer.toBinaryString(Integer.valueOf("FFFF",16));

// 十六进制转成八进制
Integer.toOctalString(Integer.valueOf("FFFF",16));

// 八进制转成十进制
Integer.valueOf("576",8).toString();

// 八进制转成二进制
Integer.toBinaryString(Integer.valueOf("23",8));

// 八进制转成十六进制
Integer.toHexString(Integer.valueOf("23",8));

// 二进制转十进制
Integer.valueOf("0101",2).toString();

// 二进制转八进制
Integer.toOctalString(Integer.parseInt("0101", 2));

// 二进制转十六进制
Integer.toHexString(Integer.parseInt("0101", 2));

知其然必先知其所以然，我们来挨个分析下。

(1) 十进制转二进制

方法为：十进制数除2取余法，即十进制数除2，余数为权位上的数，得到的商值继续除2，依此步骤继续向下运算直到商为0为止。

如150：

150 % 2 = 75 余 0
75 % 2 = 37 余 1
37 % 2 = 18 余 1
18 % 2 = 9 余 0
9 % 2 = 4 余 1
4 % 2 = 2 余 0
2 % 2 = 1 余 0
1 % 2 = 0 余 1

除到商为0为止，然后逆序。
所以150的二进制为：10010110

 

(2) 二进制转十进制

方法为：把二进制数按权展开，相加即得十进制数。

如10010110：
总共8位。

1 * 2^7 + 0 * 2^6 + 0 * 2^5 + 1 * 2^4 + 0 * 2^3 + 1 * 2^2 + 1 * 2^1 + 0 * 2^0
= 128 + 0 + 0 + 16 + 0 + 4 + 2 + 0
= 150

 

(3) 二进制转八进制

方法为：3位二进制数按权展开，相加得到1位八进制数（注意：从右向左分，分割成3位时，不足补0）。

如：10010110
010 010 110  （凑9位，第一位补0）

0 * 2^2 + 1 * 2^1 + 0 * 2^0 = 2
0 * 2^2 + 1 * 2^1 + 0 * 2^0 = 2
1 * 2^2 + 1 * 2^1 + 0 * 2^0 = 6

八进制为：226

 

(4) 八进制转二进制

方法为：八进制数通过除2取余法，得到二进制数，对每个八进制为3个二进制，不足时在最左边补零。

如：226

2 ->  2 % 2 = 1 余 0
      1 % 2 = 0 余 1
      -------- 010

2 ->  2 % 2 = 1 余 0
      1 % 2 = 0 余 1
      -------- 010

6 ->  6 % 2 = 3 余 0
      3 % 2 = 1 余 1
      1 % 2 = 0 余 1
      -------- 110

10010110 （去掉第一个的0）

 

(5) 二进制转十六进制

方法为：与二进制转八进制方法近似，八进制是取三合一，十六进制是取四合一，不足时补0（从右向左分）。

如：100101100

0001 : 0 * 2^3 + 0 * 2^2 + 0 * 2^1 + 1 * 2^0 = 1
0010 : 0 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2^0 = 2
1100 : 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 0 * 2^0 = 12

十六进制：0-9，a-f(A-F)，小a = 10, b = 11, c = 12
12超过了9，对应C

结果为：12C

 

(6) 十六进制转二进制

方法为：十六进制数通过除2取余法，得到二进制数，对每个十六进制为4个二进制，不足时在最左边补零。

如: 12C

1 : 1 % 2 = 0 余 1
    ------ 0001

2 : 2 % 2 = 1 余 0
    1 % 2 = 0 余 1
    ------ 0010

C(12): 12 % 2 = 6 余 0
       6 % 2 = 3 余 0
       3 % 2 = 1 余 1
       1 % 2 = 0 余 1
       ------- 1100

100101100

 

(7) 其他转换

十进制与八进制与十六进制之间的转换 ：

十进制转八进制或者十六进制有两种方法

第一：间接法—把十进制转成二进制，然后再由二进制转成八进制或者十六进制。

第二：把十进制转八进制或者十六进制按照除8或者16取余，直到商为0为止。

 

八进制或者十六进制转成十进制 ：

方法为：把八进制、十六进制数按权展开、相加即得十进制数。

 

十六进制与八进制之间的转换：

八进制与十六进制之间的转换有两种方法。

第一种：他们之间的转换可以先转成二进制然后再相互转换。

第二种：他们之间的转换可以先转成十进制然后再相互转换。

 

贴上测试代码：

public static void main(String[] args) {
        /**
         * 十进制转2进制，除以2，余1
         * 2进制转8进制，从右向左按3位分段，不够补0，然后与2获取结果。
         * 2进制转16进制，从右向左按4位分段，不够补0。
         */
        // ====== 十进制转二进制 =======
        int n = 298;
        /*
         * 298 % 2 = 149 ... 0
         * 149 % 2 = 74 ... 1
         * 74 % 2 = 37 ... 0
         * 37 % 2 = 18 ... 1
         * 18 % 2 = 9 ... 0
         * 9 % 2 = 4 ... 1
         * 4 % 2 = 2 ... 0
         * 2 % 2 = 1 ... 0
         * 1 % 2 = 0 ... 1
         *
         * 100101010
         */
        System.out.println(Integer.toBinaryString(n));

        // ====== 二进制转十进制 ======
        /*
         * 100110010
         *
         * 1*2^8 + 0*2^7 + 0*2^6 + 1*2^5 + 1*2^4 + 0*2^3 + 0*2^2 + 1*2^1 + 0*2^0
         * = 256 + 0 + 0 + 32 + 16 + 0 + 0 + 2 + 0
         * = 306
         */
        // Integer.valueOf最终是转成10进制输出
        System.out.println(Integer.valueOf("100110010", 2));

        // ====== 二进制转八进制 ======
        /*
         * 0110110
         *
         * 000 : 0*2^2 + 0*2^1 + 0*2^0 = 0
         * 110 : 1*2^2 + 1*2^1 + 0*2^0 = 6
         * 110 : 1*2^2 + 1*2^1 + 0*2^0 = 6
         *
         * 066，将第一个补的0去掉，最终为66
         */
        System.out.println(Integer.toOctalString(Integer.parseInt("0110110", 2)));

        // ====== 八进制转成二进制 ======
        /*
         * 53 （以0开头，0～7组成（小于8））
         *
         * 5 : 5 % 2 = 2 ... 1
         *     2 % 2 = 1 ... 0
         *     1 % 2 = 0 ... 1
         *     -------- 101
         *
         * 3 : 3 % 2 = 1 ... 1
         *     1 % 2 = 0 ... 1
         *     -------- 011
         *
         * 101011
         */
        System.out.println(Integer.toBinaryString(Integer.valueOf("53",8)));

        // ====== 二进制转十六进制 ======
        /*
         * 0111001
         *
         * 0011: 0*2^3 + 0*2^2 + 1*2^1 + 1*2^0 = 3
         * 1001: 1*2^3 + 0*2^2 + 0*2^1 + 1*2^0 = 9
         *
         * 39
         */
        System.out.println(Integer.toHexString(Integer.parseInt("0111001", 2)));

        // ====== 十六进制转二进制 ======
        /*
         * 783
         *
         * 7: 7 % 2 = 3...1
         *    3 % 2 = 1...1
         *    1 % 2 = 0...1
         *    ------ 0111
         *
         * 8: 8 % 2 = 4...0
         *    4 % 2 = 2...0
         *    2 % 2 = 1...0
         *    1 % 2 = 0...1
         *    ------ 1000
         *
         * 3: 3 % 2 = 1...1
         *    1 % 2 = 0...1
         *    ------ 0011
         *
         * 011110000011，去掉第一个补的0
         * 11110000011
         */
        System.out.println(Integer.toBinaryString(Integer.valueOf("783",16)));
    }

 

4. 进制应用实例

public final class _02_Hex_Practice {

    /**
     * Int转字节数组
     *
     * 1、(inta >> i * 8) & 0xff
     *
     * 移位 清零从左往右，按8位获取1字节。
     *
     * 2、这里使用的是小端法。地位字节放在内存低地址端，即该值的起始地址。
     * 补充：32位中分大端模式（PPC）和小段端模式（x86）。
     *
     * ------------------------------------------------------------------------------------------------------------------
     * 记得在学计算机原理的时候，了解到计算机内的存储都是利用二进制的补码进行存储的。
     *
     * 复习一下，原码反码补码这三个概念：
     *
     * 对于正数（00000001）原码来说，首位表示符号位，反码 补码都是本身
     * 对于负数（100000001）原码来说，反码是对原码除了符号位之外作取反运算即（111111110），补码是对反码作+1运算即（111111111）
     * ------------------------------------------------------------------------------------------------------------------
     * 补充：0xff
     *
     * 当将-127赋值给a[0]时候，a[0]作为一个byte类型，其计算机存储的补码是10000001（8位）。
     * 将a[0] 作为int类型向控制台输出的时候，jvm作了一个补位的处理，因为int类型是32位所以补位后的补码就是
     * 1111111111111111111111111 10000001（32位），这个32位二进制补码表示的也是-127.
     *
     * 发现没有，虽然byte->int计算机背后存储的二进制补码由10000001（8位）
     * 转化成了1111111111111111111111111 10000001（32位）很显然这两个补码表示的十进制数字依然是相同的。
     *
     * 但是我做byte->int的转化 所有时候都只是为了保持 十进制的一致性吗？
     * 不一定吧？好比我们拿到的文件流转成byte数组，难道我们关心的是byte数组的十进制的值是多少吗？我们关心的是其背后二进制存储的补码吧
     *
     * 所以大家应该能猜到为什么byte类型的数字要&0xff再赋值给int类型，其本质原因就是想保持二进制补码的一致性。
     *
     * 当byte要转化为int的时候，高的24位必然会补1，这样，其二进制补码其实已经不一致了，&0xff可以将高的24位置为0，低8位保持原样。
     * 这样做的目的就是为了保证二进制数据的一致性。
     *
     * 当然拉，保证了二进制数据性的同时，如果二进制被当作byte和int来解读，其10进制的值必然是不同的，因为符号位位置已经发生了变化。
     *
     * 象例2中，int c = a[0]&0xff;  a[0]&0xff=1111111111111111111111111 10000001&11111111=000000000000000000000000 10000001 ，
     * 这个值算一下就是129，
     *
     * 所以c的输出的值就是129。有人问为什么上面的式子中a[0]不是8位而是32位，因为当系统检测到byte可能会转化成int或者说byte与int类型进行运算的时候，
     * 就会将byte的内存空间高位补1（也就是按符号位补位）扩充到32位，再参与运算。上面的0xff其实是int类型的字面量值，所以可以说byte与int进行运算。
     * ------------------------------------------------------------------------------------------------------------------
     */
    private static byte[] int2Bytes(int inta) {
        // 32位Int可存于长度为4的字节数组
        byte[] bytes = new byte[4];
        for (int i = 0; i < bytes.length; i++) {
            // 移位和清零
            // >> 8 获取一个字节
            bytes[i] = (byte) (int) ((inta >> i * 8) & 0xff);
        }
        return bytes;
    }

    /**
     * 字节数组转Int
     */
    private static int bytes2Int(byte[] bytes) {
        int inta = 0;
        for (int i = 0; i < bytes.length; i++) {
            // 移位和清零
            inta += ((bytes[i] & 0xff) << i * 8);
        }
        return inta;
    }

    private static void test01() {
        // 将我的学号转换成字节码
        byte[] bytes = int2Bytes(1206010035);
        System.out.println(bytes[0] + " " + bytes[1] + " " + bytes[2] + " " + bytes[3]);
        // 字节码就可以转换回学号
        System.out.println(bytes2Int(bytes));
    }

    /**
     * long 转 byte数组
     */
    public static byte[] long2Bytes(long longa) {
        // 64位
        byte[] bytes = new byte[8];
        for (int i = 0; i < bytes.length; i++) {
            // 移位和清零
            // 移动8位获取一个字节，一个字节占8位
            bytes[i] = (byte) (long) (((longa) >> i * 8) & 0xff);
        }
        return bytes;
    }

    /**
     * byte数组 转 long
     */
    public static long bytes2Long(byte[] bytes) {
        long longa = 0;
        for (int i = 0; i < bytes.length; i++) {
            // 移位和清零
            longa += (long) ((bytes[i] & 0xff) << i * 8);
        }
        return longa;
    }

    public static void main(String[] args) {
        test01();
    }
}

 

5.  位运算使用

package io.kzw.advance._02_bit_hex;

/**
 * Java位运算使用.
 *
 * @author kzw on 2018/09/15.
 */
public final class _03_Bit {

    /*
     * ###### 前言
     *
     * 日常开发中位运算不是很常用，但是巧妙的使用位运算可以大量减少运行开销，优化算法。
     * 举个例子，翻转操作比较常见，比如初始值为1，操作一次变为0，再操作一次变为1。
     * 可能的做法是使用三木运算符，判断原始值为1还是0，如果是1，设置为0，否则设置为0.
     *
     * 但是使用位运算，不用判断原始值，直接改变值就可以：
     *
     * 1^num // num为原始值
     *
     * 当然，一条语句可能对代码没什么影响，但是在高重复，大数据量的情况下将会节省很多开销。
     *
     * 以下是自己整理的关于java位运算的部分内容，如有错误，还请指出，以共同进步，先行致谢。
     */
    private static void reverse() {
        int number = 1;
        for (int i = 0; i < 5; i++) {
            number = 1 ^ number;
            /*
             * 0
             * 1
             * 0
             * 1
             * 0
             */
            System.out.println(number);
        }
    }

    /*
     * ###### java支持的位运算符
     *
     * &：按位与。
     *
     * |：按位或。
     *
     * ~：按位非。
     *
     * ^：按位异或。
     *
     * <<：左位移运算符。
     *
     * >>：右位移运算符。
     *
     * <<<：无符号右移运算符。
     *
     * 位运算符中, 除～以外, 其余均为二元运算符。操作数只能为整型和字符型数据。
     *
     * Java使用 补码 来表示二进制数, 在补码表示中, 最高位为符号位, 正数的符号位为0, 负数为1。
     *
     * 补码的规定如下:
     *
     * 一、正整数的原码、反码、补码完全一样，即符号位固定为0，数值位相同
     * 二、负整数的符号位固定为1，由原码变为补码时，规则如下：
     *    1、原码符号位1不变，整数的每一位二进制数位求反，得到反码
     *    2、反码符号位1不变，反码数值位最低位加1，得到补码
     *
     *
     * 00000000000000000000000000000001  (-1)
     * 为何有那么多0、1，java中int是32位的。
     */

    /*
     * ###### 按位&
     *
     * 按位与的运算规则:
     * 0 0 1 1
     *    &
     * 0 1 0 1
     *    |
     *
     * 0 0 0 1
     *
     * 规则总结：只有两个操作数对应位同为1时，结果为1，其余全为0. （或者是只要有一个操作数为0，结果就为0）。
     */
    private static void test01() {
        /*
         * 10 & 12
         *
         * 10 % 2 = 5..0
         * 5 % 2 = 2..1
         * 2 % 2 = 1..0
         * 1 % 2 = 0..1
         * - 1010
         *
         * 同理：12 -> 1100
         * 也是补码哦
         * 1010 & 1100 = 1000
         * 转成10进制：1*2^3 + 0*2^2 + 0*2^1 + 0*2^0 = 8
         */
        System.out.println("10 & 12 = " + (10 & 12));

        /*
         * -6 & -2
         *
         * 以补码来存储，比如以8位的-6来表示，也可以是16位的，前面补1即可，凑足16位。
         *
         * -6:
         * 6 % 2 = 3..0
         * 3 % 2 = 1..1
         * 1 % 2 = 0..1
         * ---110
         *
         * 然后8位的来表示的话，前面补0，00000110
         * 取反，11111001, +1: 11111010，如果要表示成32位的，补1
         *
         * 得表示的二进制补码：11111111111111111111111111111010
         *
         * -2:
         * 2 % 2 = 1..0
         * 1 % 2 = 0..1
         * ---10
         * 00000010，取反: 11111101, +1: 11111110
         * 表示成32位：11111111111111111111111111111110
         *
         * 11111111111111111111111111111010
         *                &
         * 11111111111111111111111111111110
         *                =
         * 11111111111111111111111111111010
         *
         * 此时符号位为1，结果为补码，想求原码，需要-1取反
         * 11111111111111111111111111111001
         * 00000000000000000000000000000110
         * = 6
         * 加上符号位：-6，最终结果为-6
         *
         * 正数都是正常操作，负数就得先取补码，计算机都是补码操作，正数的补码和原码相同。
         * 补码&完成后，得到的是补码，其实正数也是一样，但是正数不需要还原。然后负数想得到原值，得 -1 取反。
         * 因为负数的补码为反码 + 1，负数的反码（除去符号位，其他位置取反）。最后得到的值，再加上符号位。
         */
        System.out.println("-6 & -2 = " + (-6 & -2));
    }

    /*
     * ###### 按位| （按位&，两个都为1则为1，按位|则是有一个为1则为1）
     *
     * 按位或的运算规则：
     * 0011
     *   |
     * 0101
     *   =
     * 0111
     *
     * 规则总结：只有两个操作数对应位同为0时，结果为0，其余全为1.（或者是只要有一个操作数为1，结果就为1）。
     */
    private static void test02() {
        /*
         * 6 | 12
         *
         * 1010 | 1100 = 1110 = 14
         */
        System.out.println("10 | 12 = " + (10 | 12));
    }

    /*
     * ###### 按位～（取反）
     *
     * 按位非的运算规则：
     * ~01 = 10
     */
    private static void test03() {
        System.out.println("~6 = " + (~6));
    }

    /*
     * ###### 按位^（异或），两个位都不相同时，则为1，相同时为0
     *
     * 按位异或的运算规则：两位不同时才为1，相同时为0
     * 0011
     *  ^
     * 0101
     *  =
     * 0110
     */
    private static void test04() {
        /*
         * 6 ^ 12
         *
         * 1010 ^ 1100 = 0110 = 6
         */
        System.out.println("10 ^ 12 = " + (10 ^ 12));
    }

    /*
     * ###### 左位移（<<，带符号）
     *
     * 规则：
     * 1）丢弃最高位，低位补0；
     * 2）如果移动位数超过了该类型的最大位数，那么编译器会对移动的位数取模操作；
     * 3）在没有溢出的情况下，对于正数和负数都相当于乘2操作；
     * 4）如果移近高级位（32/64）,那么该值将变为负数；
     */
    private static void test05() {
        /*
         * 2 << 2 = 8
         *
         * 00000010 << 2 = 00001000 = 1 * 2^3 = 8
         */
        System.out.println("2 << 2 = " + (2 << 2));
    }

    /*
     * ###### 右位移（>>，带符号）
     *
     * 规则：
     * 1）丢弃低位，高位补符号位；(负数补1，正数补0);
     * 2）对于正数和负数都相当于除2操作；
     */
    private static void test06() {
        /*
         * -6 >> 2 = -2
         *
         * -6：
         * 6 % 2 = 3..0
         * 3 % 2 = 1..1
         * 1 % 2 = 0..1
         *
         * 00000110，取反：11111001, +1 = 11111010
         *
         * -6的二进制补码为:11111010（在计算机里存储用的反码）
         *
         * 11111010>>2 = 11111110
         *
         * 注意：此时高位为1，为负数，需要取其原码才能得到它的值，如果高位为0，则不用。
         *
         * 负数求原码：-1再取反
         * -1: 11111101
         * ~: 00000010
         *
         * 得到原码：00000010 = 2
         *
         * 加上符号位: -2
         */
        System.out.println("-6 >> 2 = " + (-6 >> 2));
    }

    /*
     * ###### 无符号右移（>>>，无符号右移，只有右移才有无符号哦，丢弃高位，全部补0，0为正数，1为负数。）
     *
     * 低位移除，高位补0。
     * 注意，无符号右移（>>>）中的符号位（最高位）也跟着变，无符号的意思是将符号位当作数字位看待。
     * 如：-1>>>1结果为2147483647。这个数字应该比较熟悉，看两个输出语句就知道是什么了：
     *
     * System.out.println(Integer.toBinaryString(-1>>>1));
     * System.out.println(Integer.toBinaryString(Integer.MAX_VALUE));
     *
     * 输出结果为：
     * 1111111111111111111111111111111
     * 1111111111111111111111111111111
     *
     * -1>>>1竟然得到了int所能表示的最大整数，精彩。
     *
     * 除了使用-1>>>1能得到Integer.MAX_VALUE，以下的也能得到同样的结果：
     * //maxInt
     * System.out.println(~(1 << 31));
     * System.out.println((1 << -1)-1);
     * System.out.println(~(1 << -1));
     * 使用位运算往往能很巧妙的实现某些算法完成一些复杂的功能。
     */
    private static void test07() {
        /*
         * -6 >>> 2
         *
         * -6：
         * 6 % 2 = 3..0
         * 3 % 2 = 1..1
         * 1 % 2 = 0..1
         *
         * 00000000000000000000000000000110，取反：11111111111111111111111111111001, +1 = 11111111111111111111111111111010
         *
         * -6的二进制补码为:11111111111111111111111111111010（在计算机里存储用的反码）
         *
         * 11111111111111111111111111111010>>>2 = 00111111111111111111111111111110 = 1073741822
         *
         * 为什么上面 -6 >> 2位，与这边-6>>>2，一个用8位表示，一个用32位表示，其实int应该用32位表示，
         * 但是上面 -6 >> 2，补位完后高位为1，需要重新取反，而这边高位为1，结果无需取反。
         */
        System.out.println("-6 >>> 2 = " + (-6 >>> 2));
    }

    public static void main(String[] args) {
        /**
         * 总结：正数的反码，补码都是它本身。负数的补码为反码 + 1。
         * 计算机内部是以补码存储的。
         *
         * 高位为0为正数，高位为1为负数。
         *
         * 负数的各种位操作，得先获取负数的补码，就是取反+1，然后操作，最后得到的是补码，然后 - 1，取反，最后再加上符号就得到了结果。
         *
         * << , >>（带符号，正数高位补0，负数补1）, >>> （无符号右移，高位都补0），没有无符号<<<。
         *
         * &：都为1才为1，| ：一个为1则为1， ~:取反, ^ : 相同时为0，不同时才为1。
         */
//         reverse();
        // test01();
        // test02();
        // test03();
        // test04();
        // test05();
        // test06();
        // test07();
    }
}

 

 

6. 位运算应用实例

package io.kzw.advance._02_bit_hex;

/**
 * 位运算使用.
 *
 * @author kzw on 2018/09/15.
 */
public final class _04_Bit_Practice {

    /*
     * ###### [常见使用] 1. m * 2^n
     *
     * 可以使用m<> 32=" + (1 >> 32));
        // 1
        System.out.println("1 >> 0=" + (1 >> 0));
        // 0
        System.out.println("1 >> 31=" + (1 >> 31));
        // 0
        System.out.println("1 >> -1=" + (1 >> -1));
        // 0
        System.out.println("1 >> 30=" + (1 >> 30));
        // 0
        System.out.println("1 >> -2=" + (1 >> -2));
    }

    /*
     * ###### [常见使用] 2. 判断一个数的奇偶性
     *
     * n & 1 == 1 ? ”奇数” : ”偶数”
     *
     * 为什么与1能判断奇偶？所谓的二进制就是满2进1，那么好了，偶数的最低位肯定是0（恰好满2，对不对？），
     * 同理，奇数的最低位肯定是1.int类型的1，前31位都是0，无论是1&0还是0&0结果都是0，那么有区别的就是1的最低位上的1了，
     * 若n的二进制最低位是1（奇数）与上1，结果为1，反则结果为0.
     */
    private static void test02(int n) {
        System.out.println(n + "是 : " + ((n & 1) == 1 ? "奇数" : " 偶数"));
    }

    /*
     * ###### [常见使用] 3. 不用临时变量交换两个数
     *
     * 其实java中的异或运算法则完全遵守数学中的计算法则：
     * ①    a ^ a =0
     * ②    a ^ b =b ^ a
     * ③    a ^b ^ c = a ^ (b ^ c) = (a ^ b) ^ c;
     * ④    d = a ^b ^ c 可以推出 a = d ^ b ^ c.
     * ⑤    a ^ b ^a = b.
     */
    private static void test03() {
        int a = 3;
        int b = 4;
        a = a ^ b;
        b = b ^ a; // b = b ^ (a ^ b) --> b = a
        a = a ^ b; // (a ^ b) ^ (b ^ (a ^ b)) --> a = b
        // a = 4, b = 3
        System.out.println("a = " + a + " ,b = " + b);
    }

    /*
     * ###### [常见使用] 4. 取绝对值
     *
     * (a^(a>>31))-(a>>31)
     *
     * 先整理一下使用位运算取绝对值的思路：若a为正数，则不变，需要用异或0保持的特点；
     * 若a为负数，则其补码为源码翻转每一位后+1，先求其源码，补码-1后再翻转每一位，此时需要使用异或1具有翻转的特点。
     *
     * 任何正数右移31后只剩符号位0，最终结果为0，任何负数右移31后也只剩符号位1，溢出的31位截断，空出的31位补符号位1，
     * 最终结果为-1.右移31操作可以取得任何整数的符号位。
     *
     * 那么综合上面的步骤，可得到公式。a>>31取得a的符号，若a为正数，a>>31等于0，a^0=a，不变；若a为负数,a>>31等于-1 ，a^-1翻转每一位.
     */
    private static void test04(int n) {
        System.out.println(n + "的绝对值 = " + ((n ^ (n >> 31)) - (n >> 31)));
    }

    /*
     * ###### [常见使用] 5. 如何快速求取一个整数的7倍？
     *
     * (x<<3)-x
     */
    private static void test05(int n) {
        System.out.println(n + "的7倍 = " + ((n << 3) - n));
    }

    /*
     * ###### [常见使用] 6. 如何实现位操作求两个数的平均值?
     *
     * (x&y)+((x^y)>>1)
     */
    private static void test06(int x, int y) {
        System.out.println(x + "和" + y + "的平均值 = " + ((x & y) + ((x ^ y) >> 1)));
    }

    public static void main(String[] args) {
        // test01();
        // test02(3);
        // test02(10);
        // test03();
        // test04(-10);
        // test05(7);
        // test06(3,5);
    }
}

 

 

昨天加班，今天老况休息，但是陪了一天闺女，各种跑。上班累的是脑子，休息累的是身体，反正总得累一个。

这篇文章是我之前总结的，大部分用了源代码，算是偷个懒哈，今天晚上8点多才到家。

我的github链接：https://github.com/kuangzhongwen

代码都在里面。

明天的博客将会好好更，准备讲解下Java线程，线程的状态切换，以及线程池的原理。昨天临下班前还和同事讨论，为什么Java中的线程池，能够保证线程不死（按理线程执行完后就会死亡）。其实无外乎就是无限循环，在android framework源代码中ActivityThread，Looper, Zygote等都使用了无限循环。

 

先好好休息啦，准备明天新的一天～