传统波束形成的算法实现
最近学习了传统波束形成(CBF)的原理,尝试着写出识别一个单声源的波束形成程序。下面按照程序说明一下。
1、初始化
设置一些常数,例如抽样频率,所要计算的频率,时间步等。
clear all;
close all;
clc;
%---------初始化常量----------%
c = 334; % 声速c
fs = 1000; % 抽样频率fs
T = 0.1; % ??
t = 0:1/fs:T; % 时间 [0,0.1]
L = length(t); % 时间长度
f = 500; % 感兴趣的频率
w = 2*pi*f; % 角频率
k = w/c; % 波数 k2、阵元设置
下面是阵元部分,包括阵元个数,间距设置。
M = 18; % 阵元个数接下来是阵元坐标,声源位置,这里设置的是(12,10,12)点,同时设置阵元的高斯白噪声。
%---------各阵元坐标---------%
M = 18; % 阵元个数
% Nmid = 12; % 参考点
% d = 3; % 阵元间距
% m = (0:1:M-1)
yi = zeros(M,1); % 生成一个M*1维的零矩阵
zi = [0;3;6;9;12;15;18;21;24;12;12;12;12;12;12;12;12;12];
xi = [12;12;12;12;12;12;12;12;12;0;3;6;9;12;15;18;21;24];
%xi = xi.' % 列向量 m*d 阵元数*阵元间距
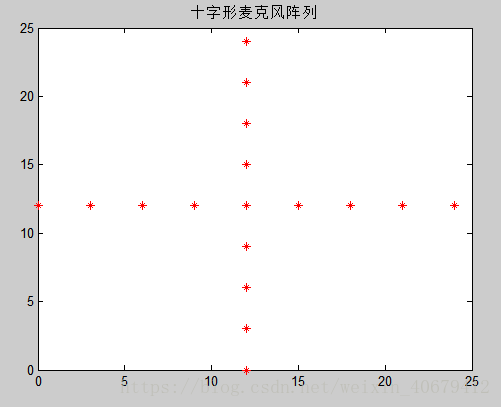
figure(1)
plot(xi,zi,'r*');
title('十字形麦克风阵列')%--------- 声源位置----------%
x1 = 12;
y1 = 10;
z1 = 12; %声源位置 (12,10,12) x,z为水平面
x2 = 12;
y2 = 0;
z2 = 12;
Ric1 = sqrt((x1-xi).^2+(y1-yi).^2+(z1-zi).^2); % 声源到各阵元的距离
Ric2 = sqrt((x1-x2).^2+(y1-y2).^2+(z1-z2).^2);
Rn1 = Ric1 - Ric2; %声源至各阵元与参考阵元的声程差矢量
s1 = cos(2*w*t); % 参考阵元接收到的矢量
Am = 10^(-1); % 振幅
n1 = Am * (randn(M,L)+j*randn(M,L)); % 各阵元高斯白噪声
p1 = zeros(M,L);
3、延迟求和
整个程序最关键的部分,延迟求和,同时得到各阵元接收的声压信号矩阵。以及协方差矩阵,这个还有疑问,要把论文读懂来理解。
%--------------------------各阵元的延迟求和--------------------------------%
for k1 = 1:M
p1(k1,:) = Ric2/Ric1(k1)*s1.*exp(-j*w*Rn1(k1)/c);
% 接收到的信号
end
p = p1+n1; % 各阵元接收的声压信号矩阵
R = p*p'/L; % 接收数据的自协方差矩阵 A.'是一般转置,A'是共轭转置
4、扫描整个声源平面
我们设置步长为0.1,扫描范围是20x20的平面,双重for循环得到M*1矢量矩阵,最后得到交叉谱矩阵(cross spectrum matrix)。由DSP理论,这个就是声音的功率。
%-------扫描范围------%
step_x = 0.1; % 步长设置为0.1
step_z = 0.1;
y = y1;
x = (9:step_x:15); % 扫描范围 9-15
z = (9:step_z:15);
for k1=1:length(z)
for k2=1:length(x)
Ri = sqrt((x(k2)-xi).^2+(y-yi).^2+(z(k1)-zi).^2);
Ri2 = sqrt((x(k2)-x2).^2+(y-y2).^2+(z(k1)-z2).^2);
% 该扫描点到各阵元的聚焦距离矢量
Rn = Ri-Ri2;
% 扫描点到各阵元与参考阵元的程差矢量
b = exp(-j*w*Rn/c); % 声压聚焦方向矢量
Pcbf(k1,k2) = abs(b'*R*b); % CSM
end
end
5、归一化处理
归一化处理的程序
%--------------------------------------归一化------------------------------%
for k1 = 1:length(z);
pp(k1) = max(Pcbf(k1,:)); % Pcbf 的第k1行的最大元素的值
end
Pcbf = Pcbf/max(pp); % 所有元素除以其最大值 归一化幅度6、作图
观察得到的结果
%-------------------------------作图展示-----------------------------------%
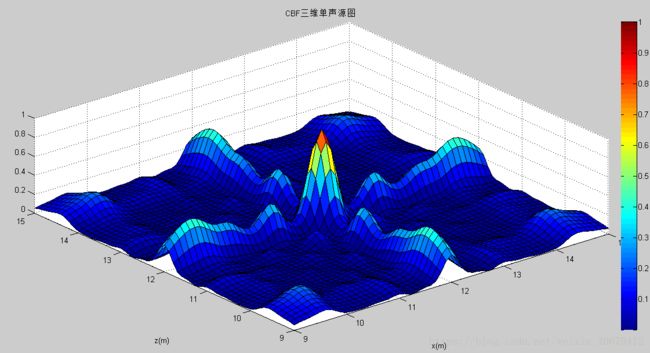
figure(2)
surf(x,z,Pcbf);
xlabel('x(m)'),ylabel('z(m)')
title('CBF三维单声源图')
colorbar
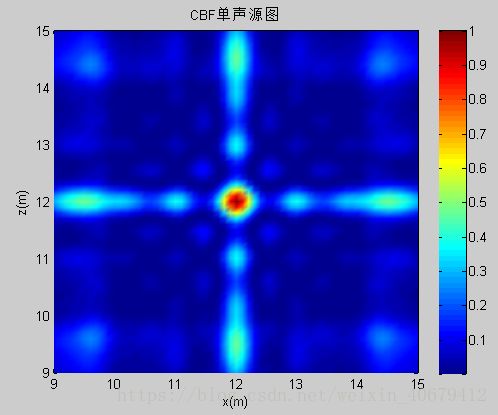
figure(3)
pcolor(x,z,Pcbf);
shading interp;
xlabel('x(m)');
ylabel('z(m)');
title('CBF单声源图')
colorbar7、结果
十字型阵列最终得到的结果效果并不理想,没有达到一个点声源的理想结果。
可以看出下图三维点声源的效果并不理想。
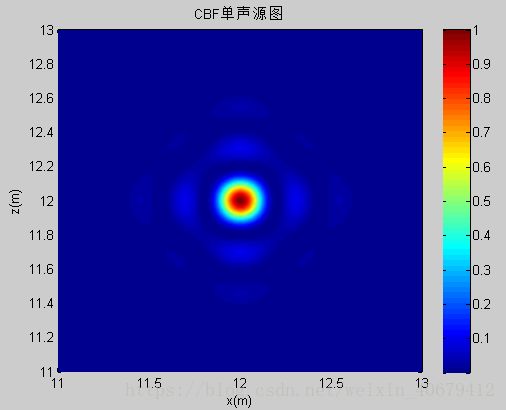
接下来是矩形阵列的结果:
可以看出下图三维点声源的效果还可以。
论文中给出的结果,很明显的点声源分布。
接下来是继续熟悉CBF算法,提高可扩展性,同时学习声源反卷积成像算法(DAMAS),下一篇进行算法总结。