数据结构基础知识
排序
参考:https://www.bilibili.com/video/av38482633/?spm_id_from=trigger_reload
目录
排序
插入排序
直接插入排序
折半排序
希尔排序
交换排序
冒泡排序
快速排序
选择排序
堆排序
流量单位计算
什么是计数排序
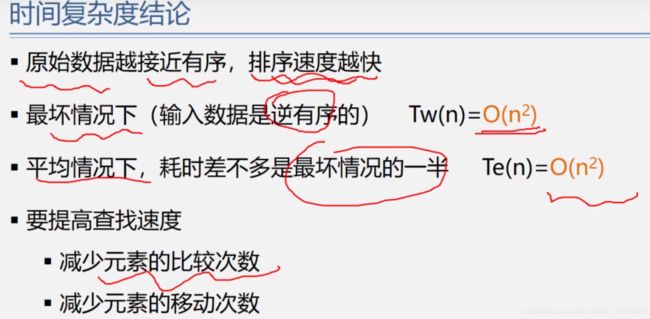
复杂度分析:
什么是基数排序?
复杂度分析(原始数列的规模是N,最大最小整数的差值是M)
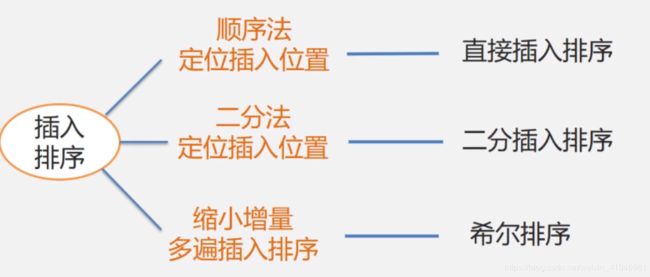
插入排序
(有序插入,在有序序列中插入一个元素,保持序列有序,有序长度增加)
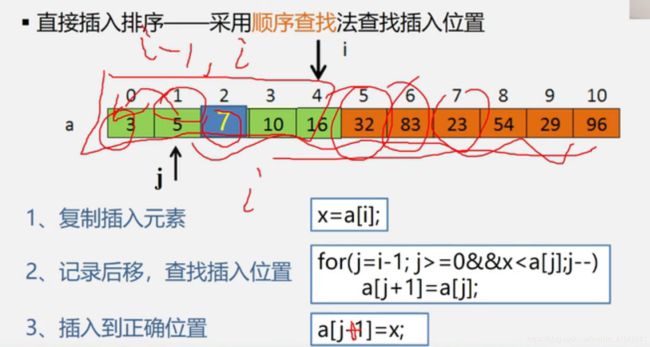
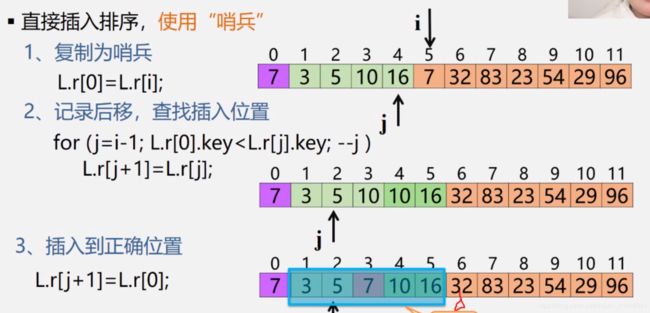
直接插入排序
——零号位为哨兵,i位要排序,顺序查找j,依次比较哨兵,大则j往后移覆盖,否则原地不动,i赋值j+1(比较后单向移动,不是交换)
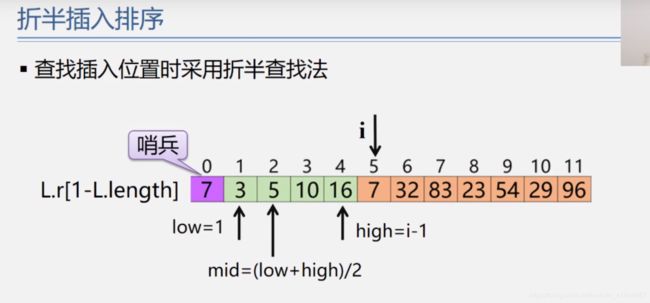
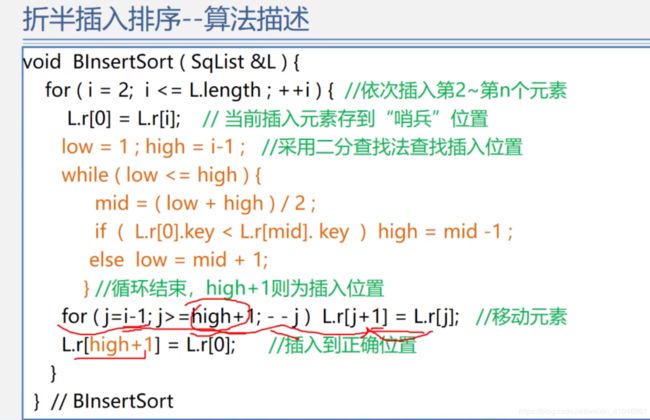
折半排序
(循环比较mid=(low+height)/ 2 与哨兵位置的大小,如果哨兵小,则到左半区查找,height=mid-1,否则右半区low=mid+1,直至low大于height,确定插入位置,然后将插入位置后面的所有对象都往后移动位置,将哨兵插入height+1)
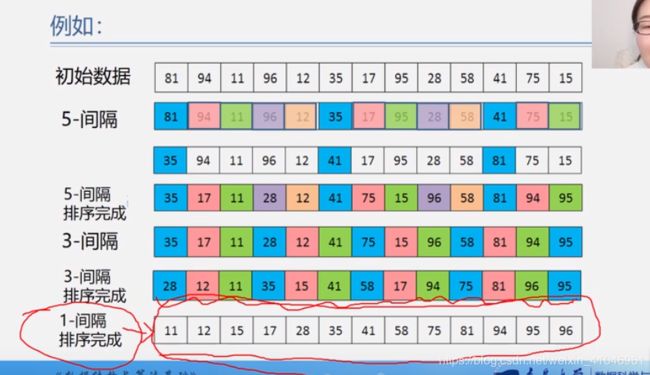
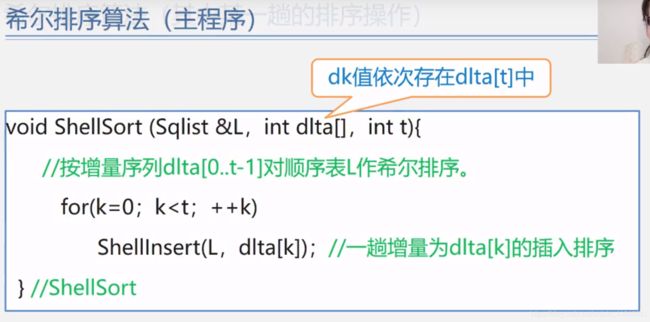
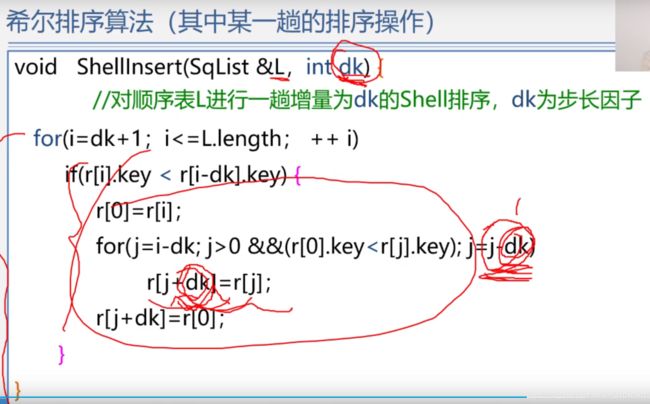
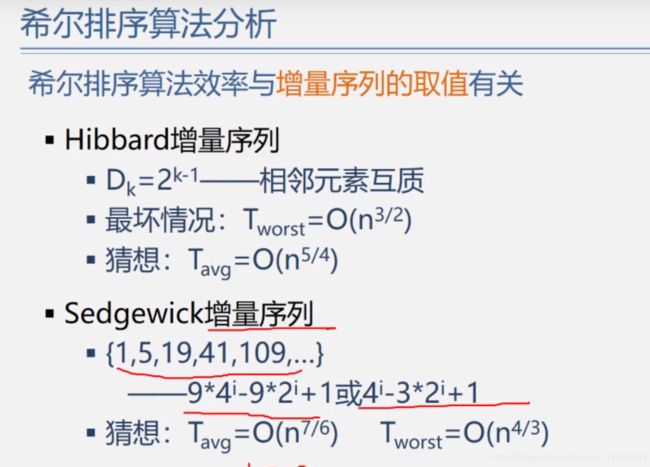
希尔排序
(算法是一步一步来的,两两对比,相隔n个数据,然后模仿直接插入排序,完事儿后接着下一个数据接着同样的以上来插入排序,最后一个间隔数值一定是1)
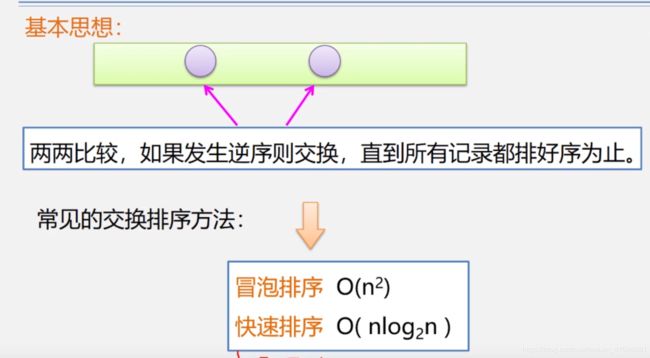
交换排序
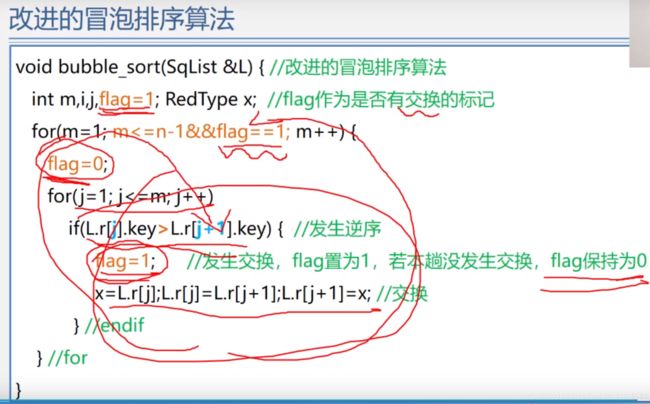
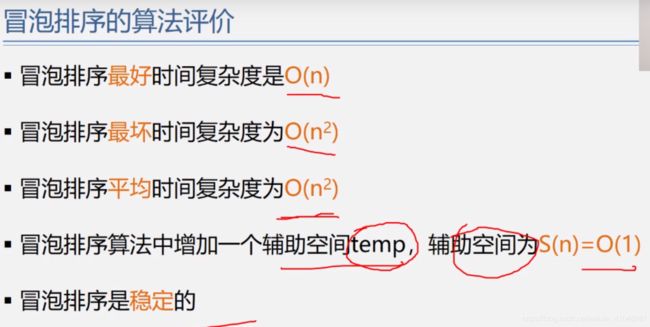
冒泡排序
(基于简单的交换思想,两两比较,大的沉底,前小后大,需要一个临时空间暂存交换操作中的元素)
![]()
如果发现一次排序后没有交换数据,那咋说明前排的数据都是有序的了,不需要再冒泡排序了
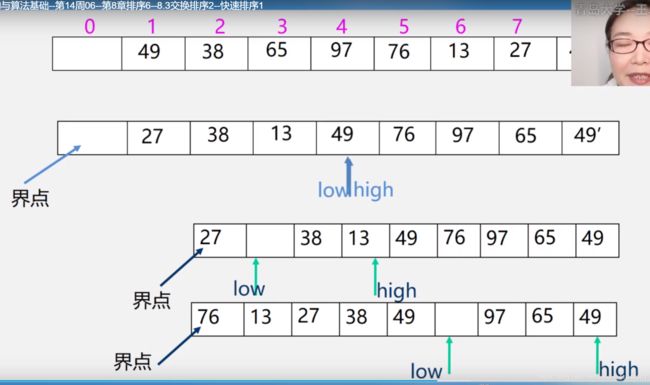
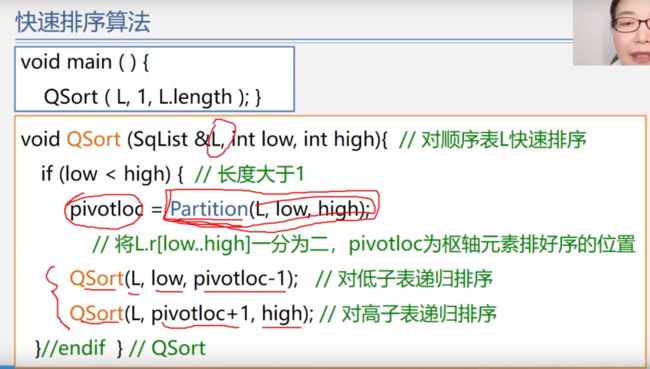
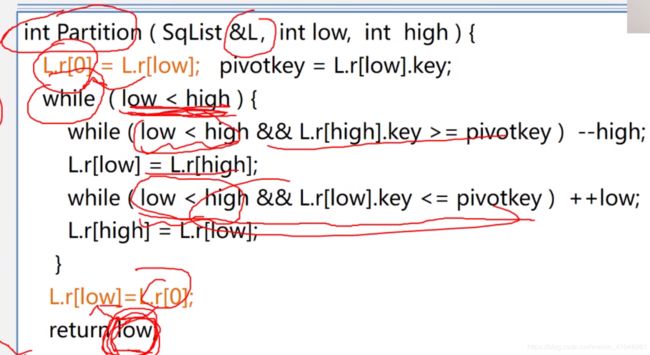
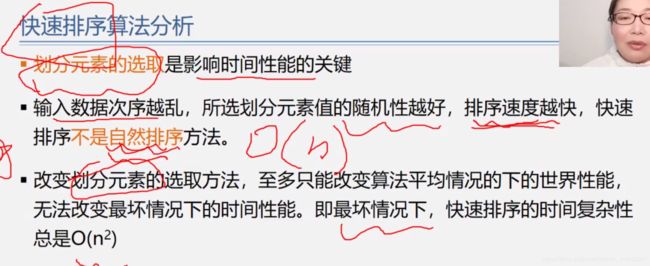
快速排序
(改进的交换排序,取中点放捎点,low、hign指针比较捎点大小分为左右区域,之后左右区域递归,不稳定)
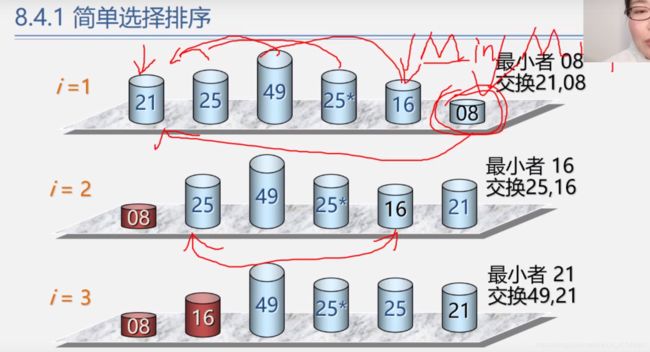
选择排序
简单选择排序(选择未排序里最小的并与第一个进行交换,之后依次步骤一样)
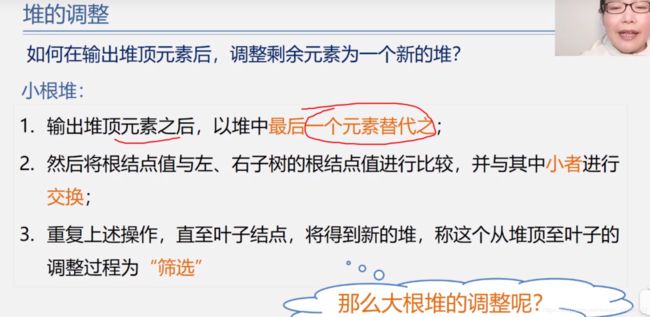
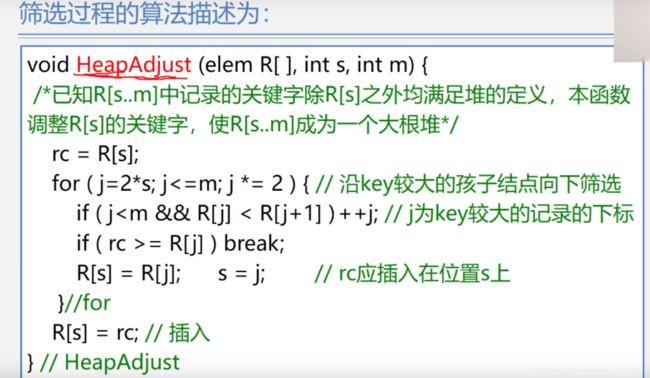
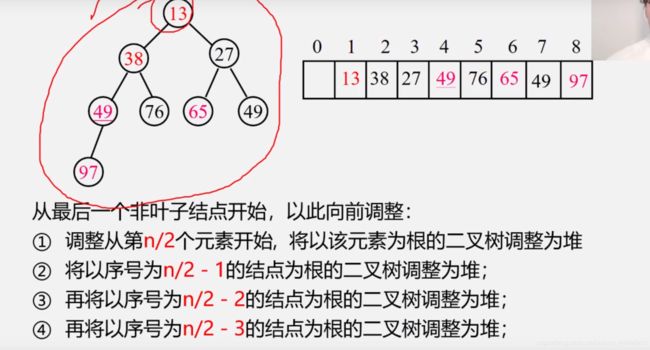
堆排序
无序的话就按数组顺序,由根往下排,并从第一个非叶子节点(n/2 | 0)开始堆调整,直至符合堆的定义
流量单位计算
流量单位G,M,K,B,是什么意思?
G, M, K, B, 都是数据或数据流量的单位符号。
其中,B 是字节的符号,字节 是数据或数据流量的基本单位。 它们之间的换算关系是:
它们之间的换算关系是: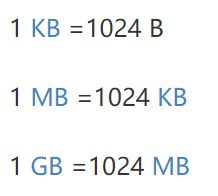
什么是计数排序
先考一道算法题:
数组里有20个随机整数,取值范圉从0到10,要求用最快的速度把这20个整数从小到大进行排序。有没有比快速排序 0( nlogn)更快的排序方法呢?有的,就是用计数排序。
让我们先来回顾一下咱们以前所学过的排序算法,无论是冒泡排序,还是快速排序等等,都是基于元素之间的比较来进行排序。有一种特殊的排序算法叫做【计数排序】,这种排序算法不是基于元素比较,而是利用数组下标来确定元素的正确位置。
基于上题中,整数的取值范围只是从0-10之间,让我们根据这个整数取值范围,建立一个长度为11的数组。数组下标从0到10,元素初始值全为0。
假定20个随机整数的值如下
9,3,5,4,9,1,2,7,8,1,3,6,5,3,4,0,10,9,7,9
如何给这些无序的随机整数排序呢?
非常简单,让我们遍历这个无序的随机数列,每一个整数按照其值对号入座,对应数组下标的元素进行加1操作。
比如第一个整数是9,那么数组下标为9的元素加1:
第二个整数是3,那么数组下标为3的元素加1:
最终,数列遍历完毕时,数组的状态如下
数组每一个下标位置的值,代表了数列中对应整数出现的次数
有了这个“统计结果”,排序就很简单了。直接遍历数组,输出数组元素的下标值,
元素的值是几,就输出几次
0,1,1,2,3,3,3,4,4,5,5,6,7,7,8,9,9,9,9,10
显然,这个输出的数列已经是有序的了。
这就是计数排序的基本过程,它适用于一定范围的整数排序。在取值范围不是很大的情况下,它的性能甚至快过那些0(nlogn)的排序。
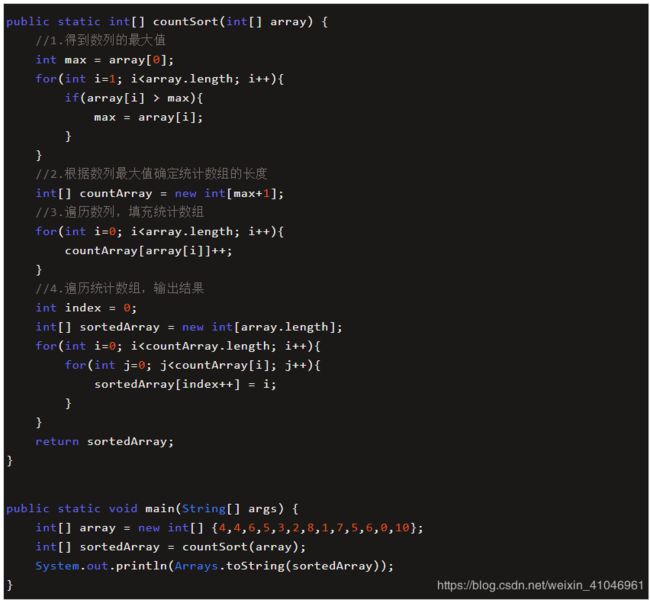
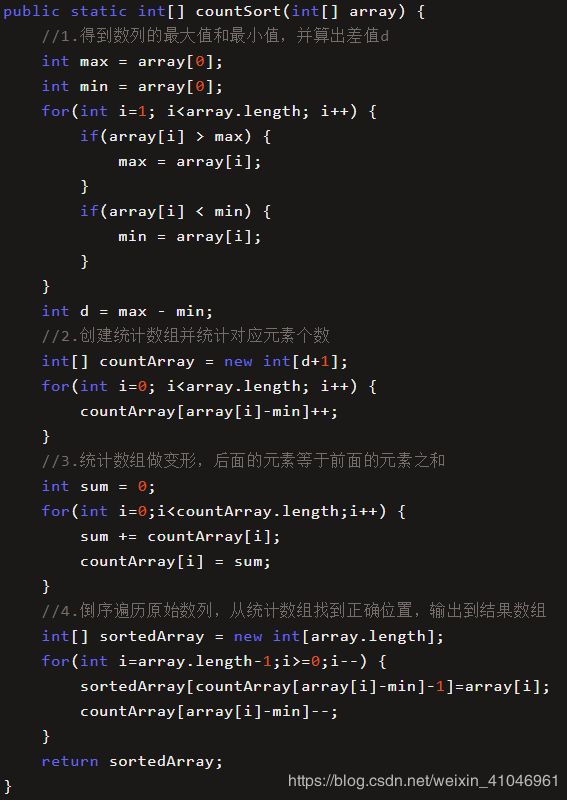
初步代码如下:
这段代码在一开头补充了一 一个步骤,就是求得数列的最大整数值max。后面创建的统计数组countArray ,长度就是max+1 ,以此保证数组的最后-一个下标是max。
只以数列的最大值来决定统计数组的长度,其实并不严谨。而应该以最大值和最小值的差来作为数组的大小。不然会浪费空间。
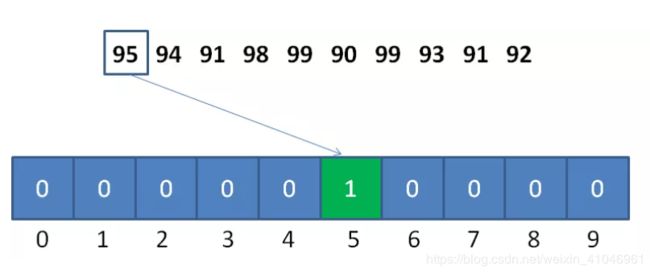
我们不再以(输入数列的最大值+1 )作为统计数组的长度,而是以(数列最大值和最小值的差+1 )作为统计数组的长度。同时,数列的最小值作为-一个偏移量,用于统计数组的对号入座。

以这个数列为例,统计数组的长度为99-90+1 = 10 , 偏移量等于数列的最小值90。对于第一个整数95 ,对应的统计数组下标是95-90 = 5 ,如图所示:
此外,朴素版的计数排序只是简单地按照统计数组的下标输出了元素值,并没有真正给原始数列进行排序。
如果是单纯的给整数排序,这样并没有问题。但如果放在现实业务里,比如给学生的考试分数排序,遇到相同的分数就会分不清谁是谁。
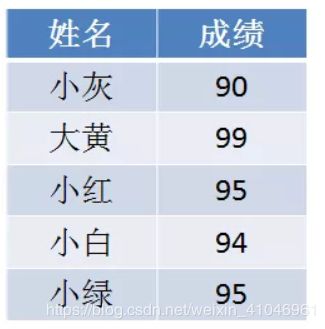
给定一个学生的成绩表,要求按成绩从低到高排序,如果成绩相同,则遵循原表固有顺序。
那么,当我们填充统计数组以后,我们只知道有两个成绩并列95分的小伙伴,却不知道哪一个是小红,哪一一个是小绿:
我们需要稍微改变之前的逻辑,在填充完统计数组以后,对统计数组做一下变形。![]()
统计数组从第二个元素开始,每一个元素都加上前面所有元素之和。
这样相加的目的,是让统计数组存储的元素值,等于相应整数的最终排序位置。比如下标是9的元素值为5,代表原始数列的整数9,最终的排序是在第5位。
接下来,我们创建输出数组sortedArray,长度和输入数列一致。然后从后向前遍历输入数列:
第一步,我们遍历成绩表最后一行的小绿:
小绿是95分,我们找到countArray下标是5的元素,值是4,代表小绿的成绩排名位置在第4位。(位置下标是3,因为成绩最少的是第一位,而他下标的位置对应就是0)
同时,我们给countArray下标是5的元素值减1,从4变成3,,代表着下次再遇到95分的成绩时,最终排名是第3。
这样一来,同样是95分的小红和小绿就能够清楚地排出顺序了,也正因此,优化版本的计数排序属于稳定排序。
![]()
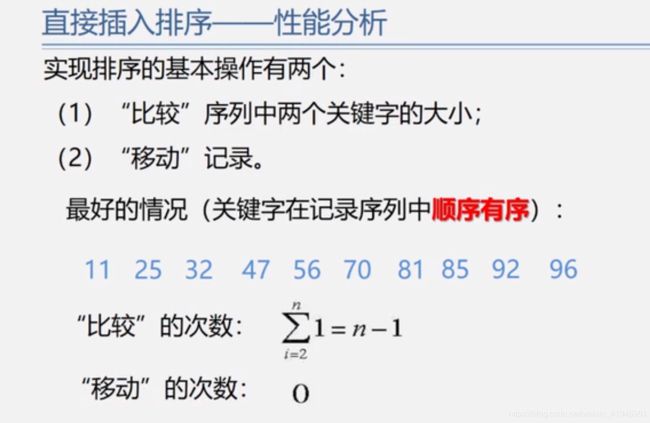
复杂度分析:
如果原始数列的规模是N,最大最小整数的差值是M,你说说计数排序的时间复杂度和空间复杂度是多少?
代码第1, 2, 4步都涉及到遍历原始数列,运算量都是N,第3步遍历统计数列,运算量是M,所以总体运算量是3N+M,去掉系数,时间复杂度是0 (N+M)。
至于空间复杂度,如果不考虑结果数组,只考虑统计数组大小的话,空间复杂度是0 (M) 。
而计数排序存在它的局限性,主要表现在两点:
1.当数列最大最小值差距过大时,并不适用计数排序。
比如给定20个随机整数,范围在0到1亿之间,这时候如果使用计数排序,需要创建长度1亿的数组。不但严重浪费空间,而且时间复杂度也随之升高。
2.当数列元素不是整数,并不适用计数排序。
如果数列中的元素都是小数,比如25.213,或是0.00000001这样子,则无法创建对应的统计数组。这样显然无法进行计数排序。
对于这些局限性,另一种线性时间排序算法做出了弥补,这种排序算法叫做[桶排序],我们后续将会讲到。
参考: 什么是计数排序?
什么是基数排序?
让我们接着来看两个特殊的需求:
需求 A,为一组给定的手机号排序:
18914021920
13223132981
13566632981
13660891039
13361323035
........
........
按照计数排序的思路,我们要根据手机号的取值范围,创建一个空数组。
可是,11 位手机号有多少种组合?恐怕要建立一个大得不可想象的数组,才能装下所有可能出现的 11 位手机号!
需求 B,为一组英文单词排序:
banana
apple
orange
peach
cherry
........
........
计数排序适合的场景是对整数做排序,如果遇到英文单词,就无能为力了。
如何有效处理诸如手机号、英文单词等复杂元素的排序呢?仅仅靠一次计数排序很难实现。
这时候,我们不妨把排序工作拆分成多个阶段,每一个阶段只根据一个字符进行计数排序,一共排序 k 轮(k 是元素长度)。
或许这样的描述有些抽象,我们来举一个例子。
数组中有若干个字符串元素,每个字符串元素都是由三个英文字母组成:
bda,cfd,qwe,yui,abc,rrr,uee
如何将这些字符串按照字母顺序排序呢?
由于每个字符串的长度是 3 个字符,我们可以把排序工作拆分成 3 轮:
第一轮:按照最低位字符排序。排序过程使用计数排序,把字母的 ascii 码对应到数组下标,第一轮排序结果如下:
![]()
第二轮:在第一轮排序结果的基础上,按照第二位字符排序。
![]()
需要注意的是,这里使用的计数排序必须是稳定排序,这样才能保证第一轮排出的先后顺序在第二轮还能继续保持。
比如在第一轮排序后,元素 uue 在元素 yui 之前。那么第二轮排序时,两者的第二位字符虽然同样是 u,但先后顺序万万不能变,否则第一轮排序就白做了。
第三轮:在第二轮排序结果的基础上,按照最高位字符排序。
如此一来,这些字符串的顺序就排好了。
像这样把字符串元素按位拆分,每一位进行一次计数排序的算法,就是基数排序(Radix Sort)。
基数排序既可以从高位优先进行排序(Most Significant Digit first,简称MSD),也可以从低位优先进行排序(Least Significant Digit first,简称LSD)。
不过,如果排序的字符串长度不规则呢?这个问题不难解决。我们以最长的字符串为准,其他度不足的字符串,在末尾补0即可。在排序时,我们把字符 0 当做是比 a 更小的字符,排序结果如下:
ape000
apple0
banana
he0000
orange
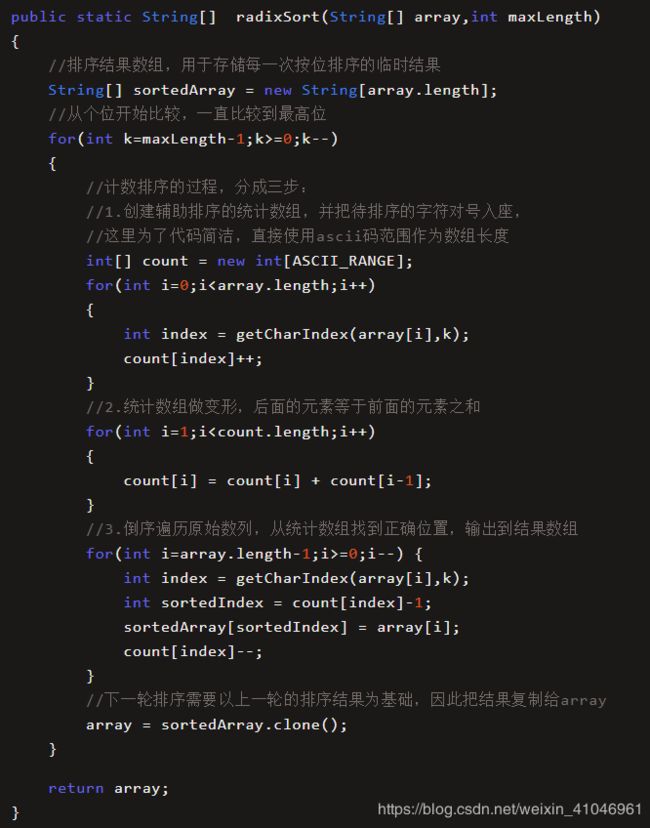
代码如下:
备注:
ASCII ((American Standard Code for Information Interchange): 美国信息交换标准代码)是基于拉丁字母的一套电脑编码系统,主要用于显示现代英语和其他西欧语言。它是最通用的信息交换标准,并等同于国际标准ISO/IEC 646。ASCII到目前为止共定义了128个字符 。
空字符的ASCII码如下:
![]()
这段代码基于一个大循环来实现,循环进行 k 次,k 就是数组中最长字符串元素的字符数。
复杂度分析(原始数列的规模是N,最大最小整数的差值是M)
原本计数排序的时间复杂度是0 (n+m),而基数排序总共执行了k次计数排序,所以时间复杂度是0 (k (n+m)),其中k是字符串的最大长度, m是字符范围。
至于空间复杂度,由于基数排序的辅助数组是反复重用的,所以基数排序的空间复杂度和计数排序-样,都是0(n+m),其中m是字符的取值范围大小。
参考:什么是基数排序?