（Java）leetcode-42 Trapping Rain Water（接雨水）

题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

注：下面的解法整理自leetcode windliang大佬的题解

思路1：东张西望

我们分别求每一列能装多少水。

求每一列的水，我们只需要关注3列：当前列，以及左边最高的列，右边最高的列就够了。

因为这3列的高度决定了当前列能装多少水，与其他列无关。

装水的多少，根据木桶效应，我们只需要看左边最高的墙和右边最高的墙中较矮的一个就够了。

所以，根据较矮的那个墙和当前列的墙的高度可以分为三种情况。

1. 较矮的墙的高度大于当前列的墙的高度
2. 较矮的墙的高度小于当前列的墙的高度
3. 较矮的墙的高度等于当前列的墙的高度

下面就这3种情况分类讨论。

• （1）较矮的墙的高度大于当前列的墙的高度
  
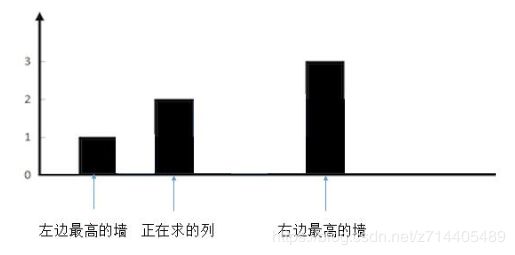
  把正在求的列左边最高的墙和右边最高的墙确定后，为了方便理解，我们把无关的墙去掉，因为留下的三列的高度决定了当前列能装多少水，与其他列无关。去掉干扰后如下图所示：
  
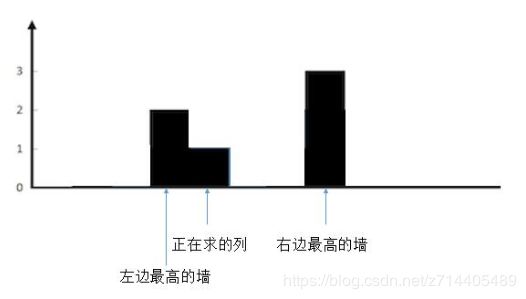
  这样就很清楚了，现在想象一下，往两边最高的墙之间注水。正在求的列会有多少水？

很明显， 较矮的一边，也就是左边的墙的高度，减去 当前列 的高度就可以了，也就是 2 - 1 = 1，可以存一个单位的水。

也就是说，对于较矮的墙的高度大于当前列的墙的高度，计算方法为 矮墙高 - 当前高。

• （2）较矮的墙的高度小于当前列的墙的高度
  去掉干扰后如下图所示：
  
  正在求的列不会有水，因为它大于了两边较矮的墙。因此，对于这种情况，不需要再计算水量了。

• （3）较矮的墙的高度等于当前列的墙的高度

和上一种情况是一样的，不会有水。

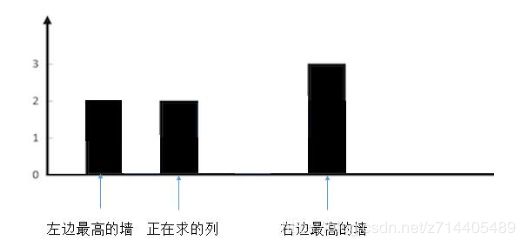
明白了这三种情况，程序就很好写了，遍历每一列，然后分别求出这一列两边最高的墙。找出较矮的一端，和当前列的高度比较，结果就是上边的三种情况。

时间复杂度：O(n²），遍历每一列需要 n，处理其中的任意列，需要找出左边最高和右边最高的墙加起来刚好也是一趟遍历，又是一个 n，所以是 n²。

空间复杂度：O(1）。

class Solution {
	public int trap(int[] height) {
	    int sum = 0;
	    // 最两端的列不用考虑，因为一定不会有水。所以下标从 1 到 length - 2
	    for (int i = 1; i < height.length - 1; i++) {
	        int max_left = 0;
	        // 找出左边最高
	        for (int j = i - 1; j >= 0; j--) {
	            if (height[j] > max_left) {
	                max_left = height[j];
	            }
	        }
	        
	        int max_right = 0;
	        // 找出右边最高
	        for (int j = i + 1; j < height.length; j++) {
	            if (height[j] > max_right) {
	                max_right = height[j];
	            }
	        }
	        
	        // 高个里面挑矮子，找到两边高墙中的较小值
	        int min = Math.min(max_left, max_right);
	        
	        // 只有较小的一段大于当前列的高度才会有水，其他情况不会有水
	        if (min > height[i]) {
	            sum = sum + (min - height[i]);
	        }
	    }
	    return sum;
	}
}

执行用时：83 ms, 在所有 Java 提交中击败了11.49%的用户
内存消耗：39.7 MB, 在所有 Java 提交中击败了12.86%的用户

思路2：动态规划

我们注意到，解法二中。对于每一列，我们求它左边最高的墙和右边最高的墙，都是重新遍历一遍所有高度，这里我们可以优化一下。

首先用两个数组，max_left [i] 代表第 i 列左边最高的墙的高度，max_right[i] 代表第 i 列右边最高的墙的高度。（不包括第 i 列自身）

对于 max_left我们其实可以这样求。

max_left [i] = Max(max_left [i-1], height[i-1])
求当前列左边最高的墙max_left [i]，要么是其左边墙 height[i-1]，要么是其左边墙的 max_left [i-1]。

同理，对于 max_right我们可以这样求。

max_right[i] = Max(max_right[i+1], height[i+1]) 。

这样，我们再利用解法二的算法，就不用在 for 循环里每次重新遍历一次求 max_left 和 max_right 了，而是提前遍历两趟来获取对应的数据，最后再通过一趟遍历来计算能装多少水。

时间复杂度：O(n)。只需花费3n，因此时间复杂度是线性的。

空间复杂度：O(n)，用来保存每一列左边最高的墙和右边最高的墙所花费的数组空间。

class Solution {
	public int trap(int[] height) {
	    int sum = 0;
	    int[] max_left = new int[height.length];
	    int[] max_right = new int[height.length];
	    
	    // 从左到右把数组max_left中的值求出来
	    for (int i = 1; i < height.length - 1; i++) {
	        max_left[i] = Math.max(max_left[i - 1], height[i - 1]);
	    }
	    // 从右到左把数组max_right中的值求出来
	    for (int i = height.length - 2; i >= 0; i--) {
	        max_right[i] = Math.max(max_right[i + 1], height[i + 1]);
	    }

	    // 遍历数组，分别求每一列的水
	    for (int i = 1; i < height.length - 1; i++) {
	    	// 高个里面挑矮子，找到两边高墙中的较小值
	        int min = Math.min(max_left[i], max_right[i]);

	        // 只有较小的一段大于当前列的高度才会有水，其他情况不会有水
	        if (min > height[i]) {
	            sum = sum + (min - height[i]);
	        }
	    }
	    return sum;
	}
}

执行用时：1 ms, 在所有 Java 提交中击败了99.98%的用户
内存消耗：39 MB, 在所有 Java 提交中击败了12.86%的用户

思路3：双指针

动态规划中，我们常常可以对空间复杂度进行进一步的优化。

例如这道题中，可以看到，max_left [ i ] 和 max_right [ i ] 数组中的元素我们其实只用一次，然后就再也不会用到了。所以我们可以不用2个数组，改为用2个元素，分别维护左、右最大值。

本思路使用 双指针，从两侧往中间推进。处理一侧指针指向位置的水量时，先找到当前维护的左、右最大值中较小的那个，按前面的思路计算水量后，往中间移动指针。左值较小，推进左指针，右值较小，推进右指针。（有点类似快排）

例如，当前 i 处左边的最大值如果比右边的小，那么就可以不用考虑 i 处右边最大值的影响了，因为 i 处 右边真正的最大值绝对比左边的最大值要大。在不断遍历时，更新max_l和max_r以及结果值即可。此外，处理完i处后，应该推进的指针是左指针，直到右最大值小于左（因为左最大值一直在更新，有可能超过右大值），此时较小的最大值max_l变为了max_r，才会推进右指针。

左右指针相遇时，遍历结束。

例 [0,1,0,2,1,0,1,3,2,1,2,1]中i=2时，值为0，此时max_l一定为1，当前max_r如果为2，即便max_r不是真正的i右边的最大值，也可忽略右边最大值的影响，因为右边真正的最大值一定比左边真正的最大值大。

时间复杂度： O(n)。
空间复杂度： O(1)。

class Solution {
    public int trap(int[] height) {
    	// 左指针
        int left = 0;
        // 右指针
        int right = height.length - 1;
        
        // 左边的最大值
        int max_l = 0;
        // 右边的最大值
        int max_r = 0;
        int res = 0;

        // 左右指针相遇则循环结束
        while(left <= right){
        	// 左大值小于右大值，则水量取决于左大值
            if(max_l < max_r) {
            	// 如果左大值大于当前列的高度才会有水，其他情况不会有水
                if(max_l > height[left]) res += max_l - height[left];
                // 否则左大值小于当前列高度，则更新左大值
                else max_l = height[left];
                // 左指针往右移动
                left++;
            } else {
            	// 左大值大于右大值，则水量取决于右大值
            	// 如果右大值大于当前列的高度才会有水，其他情况不会有水
                if(max_r > height[right]) res += max_r - height[right];
                // 否则右大值小于当前列高度，则更新右大值
                else max_r = height[right];
                // 右指针往左移动
                right--;
            }
        }
        return res;
    }
    
}

执行用时：1 ms, 在所有 Java 提交中击败了99.98%的用户
内存消耗：39.8 MB, 在所有 Java 提交中击败了12.86%的用户

思路4：栈

待补充…