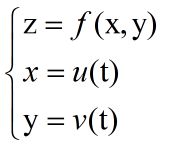偏导数,全导数,方向导数,偏微分,全微分,梯度
学习到机器学习线性回归和逻辑回归时遇到了梯度下降算法,然后顺着扯出了一堆高数的相关概念理论:导数、偏导数、全微分、方向导数、梯度,重新回顾它们之间的一些关系,从网上和教材中摘录相关知识点。
这段是我的简单总结,如果看不懂没关系,先看下面的定义
- 通过函数的极限定义出导数(以一元函数为例)
- 函数f(x)在点x0可微的充分必要条件是函数f(x)在点x0处可导
- 扩展到多元函数时,衍生出偏导数
全导数
请参考马同学的这个回答:https://www.zhihu.com/question/26966355,他这篇文章还是较为适合有一定基础的人看的,我推荐先将我所有的内容看完再去看这篇文章才能get到一些点。
从上面这个公式可以看出z是一个二元函数,如果不加下面的2个条件,那么z是没有全导数的。但是如果加了下面2个条件,则z就存在全导数,这时称z关于t的导数就是全导数。可以看出他本质上就是一个一元函数,因此全导数只是针对真正的一元函数而言,也就是z中所有的变量x和y都可以用同一个t来表示。对于真正的多元函数是没有全导数这一说的,只有偏导数、偏微分和全微分。
我将全导数放在分割线前是由于全导数对t求导数时,它实际上就是一个一元函数,那么就应该被分到一元函数的区间内。
全导数和全微分是完全不同,全微分是针对多元函数的。
这里往上是单变量(即一元函数)的导数和微分:
导数本质是一种极限,实际场景中表示切线斜率;
微分本质是“以值代曲,线性逼近”,让本来对曲线进行运算的操作,转化成对直线进行操作,简化了难度。
单变量(即一元函数)的导数和微分的关系:
我认为这两个的出发点是不一样的,导数是为了求斜率,就是该点的瞬间变化情况;微分是为了将问题简化,用直线代替曲线,线性逼近,毕竟对直线(或线段)的研究是相对容易的,而曲线就相对较难。
单变量导数 <=> 单变量微分(即单变量导数和单变量微分互为充分必要)。
---------------------------------------------------------这里是一道华丽的分割线--------------------------------------------------------
这里往下是多变量的导数和微分(涉及概念:偏导数,偏微分,全微分,方向导数,梯度):
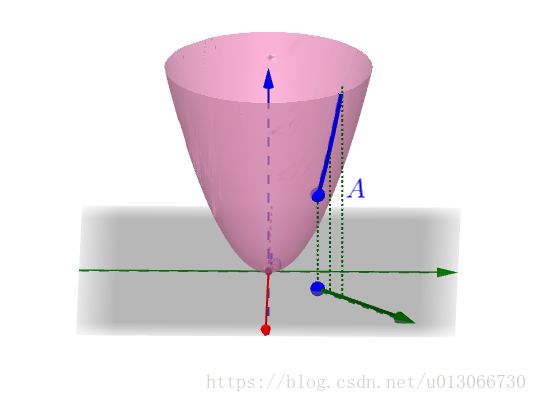
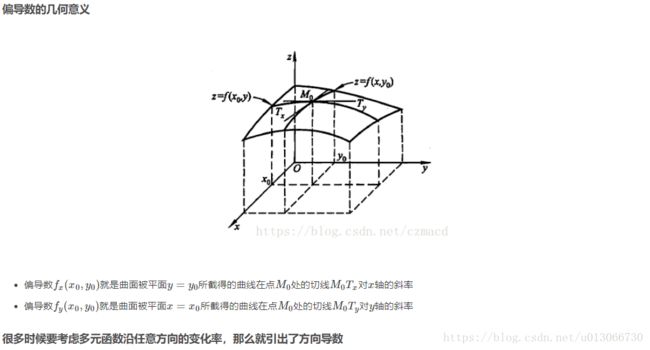
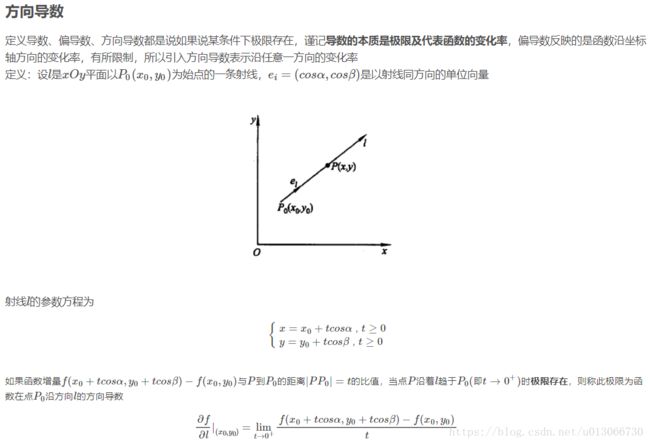
偏导数其实和导数一样,仅仅是进行了一个扩展,从原来的一元函数扩展到多元函数,这时就有了偏导数的概念。偏导数和导数一样都是表示切线的斜率。偏导数只是针对变元(这里的变元是指多元函数中的某一元)的导数。这时就需要引出一个方向导数了,我们用一个实例还说明为什么需要方向导数。比如一个二元函数,具体公式如下所示,
具体的形状如图所示:
其中A点可以有在xy平面内的(为啥是xy平面呢,我还没有找到一个合理的解释,让我再想想)任意方向的导数。其中有一个方向的导数是变化是最快的,那么这个方向就是梯度的方向,模长就是梯度大小。
偏微分和偏导数的出发点不同,偏导数是变化率,偏微分是某一变元的增量给z带来的变化,只不过在某一变元的增量特别小时,可以借用导数的计算方法,但并不是导数。
全微分是针对所有变元的增量给z带来的变化,是从偏微分拓展而来。
补充
梯度是向量,微分是一个数值。
设u=u(x,y,z),首先三维中梯度的定义是gradu=iðu/ðx+jðu/ðy+kðu/ðz,它是一个向量,而全微分du=(ðu/ðx)dx+(ðu/ðy)dy+(ðu/ðz)dz,是用坐标的微小增量dx、dy、dz表示函数u的增量,是一个表达式,和矢量无关,也和切线无关。
下面来说明梯度为什么和切向量(一维切向量就是切线,二维切向量就是切平面)垂直,设曲线x=x(t),y=y(t),z=z(t)是曲面u(x,y,z)=c上的一条曲线(c为常数,u(x,y,z)=c表示等值面),由于该曲线在曲面上,所以x=x(t),y=y(t),z=z(t)满足方程u(x,y,z)=c,即u(x(t),y(t),z(t))=c,利用复合函数求导法则,方程两边同时对t求导数,得 (ðu/ðx)*x‘(t)+(ðu/ðy)*y‘(t)+(ðu/ðz)*z‘(t)=0,所以向量(x'(t),y'(t),z'(t))与向量(ðu/ðx,ðu/ðy,ðu/ðz)垂直。而向量(x'(t),y'(t),z'(t))表示曲线的切向量,向量(ðu/ðx,ðu/ðy,ðu/ðz)表示梯度,所以梯度和切向量垂直。函数u在一点的梯度是一个向量,它的方向是函数u在该点方向导数取得最大值时的方向,它的模等于方向导数的最大值。
全微分与偏导数、偏微分的关系
- 全微分存在偏导数、偏微分一定存在
- 偏导数、偏微分存在全微分不一定存在
https://www.zhihu.com/question/26966355
https://blog.csdn.net/fffupeng/article/details/73522425
https://blog.csdn.net/qq_41455420/article/details/79661885?utm_source=blogxgwz2
https://blog.csdn.net/czmacd/article/details/81178650
https://blog.csdn.net/u013066730/article/details/83151829
导数的理解:https://www.zhihu.com/question/28684811