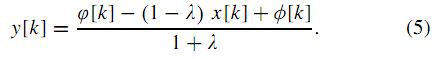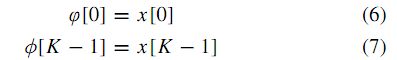说起为什么会看到这个东西,那还真的绕一圈。首先在写《Single Image Haze Removal Using Dark Channel Prior》一文中图像去雾算法的原理、实现、效果及其他。 一文时里面提到了导向滤波,然后看何凯明的《Guided Image Filtering》一文时又多次提到双边滤波,结果我就又把以前研究的双边滤波的文章翻出来看看,就再次翻到了Fast O(1) bilateral filtering using trigonometric range kernels 一文,在论文的第10页有如下这段文字:
The Java source code can be downloaded from the web at http://bigwww.epfl.ch/algorithms/bilateral-filter
我试着打开这个网页,结果遇到了CSDN常见的404错误,然后想既然来了,就在这个网站多看看,哇,原来这个真是个好网站,有大量的图像算法可以学习。一眼我就看到了最左侧有一个Download Algorithms项目,于是进去瞧瞧,并在浏览器里搜索bilateral,结果的确搜到了于有关bilateral的一个代码,如下所示:
BEEPS. This ImageJ plugin smoothes an image without altering its edges. The smoothing is applied by the way of a bi-exponential filter, itself realized by a pair of one-tap recursions. It is therefore very fast; moreover, its computational cost is truly independent of the amount of smoothing. Meanwhile, the preservation of edges is obtained by a range filter akin to the range filter found in a bilateral filter。
初步一看,我以为是作者对论文又有了新了改进,于是下载代码,并试着将这个插件安装到ImageJ中,运行后,效果和运行速度果然不错,但是,仔细看论文,确发现和上述的快速双边滤波不是一回事。
好了,言归正文。BEEPS,是Bi-Exponential Edge-Preserving Smoother 一文各字母的缩写,这篇文章里涉及到了很多数学理论,比如Z变换等等,这些我都基本上已经丢给老师了,不过不要紧,那些验证工作是写论文的这些牛人们需要去做的工作。我们最关心的是算法的流程。 幸好在这篇论文中,算法的流程在算法的第二页就已经完全的展示了, 并且过程特别简单,为避免翻译错误,先直接贴原文:
The first recursion is progressive. Letting x[k] be the current sample of an input sequence x at location k ∈ Z,were cursively compute the elements of an auxiliary sequence ϕ as:
![]()
where:
![]()
The second recursion is regressive and very similar to thefirst one, except for a reversal of the order in which the indices are traversed. We recursively compute a second auxiliary sequence φ as:
![]()
where:
![]()
We complete our algorithm by merging the resulting progressive sequence ϕ and regressive sequence φ to produce the samples of the output sequence y as:
We propose the trivial choice:
小注:博客园团队建议我用他们内置的公式编辑器输入公式,我看还是算了吧,那个东西还需要记忆一堆东西,不如直接贴图来的快又准确。
对上述过程稍作解释:x[k]可以看做是已经离散后的输入数据,λ ∈[0,1)是一个用户输入的用来控制空域滤波的程度,r是一个双变量的函数,用于控制值域滤波系数,对于双边滤波,该函数可取经典的高斯分布函数,也可以取其他的函数。
上述过程就是一个简单的前向迭代和反向迭代,然后再按一定的规则去平均值的过程。因此计算非常简单。
但是上述是个一维的过程,对于二维的图像数据,论文中也给出了解决方式,首先:对图像数据进行一次水平迭代计算,然后再对该数据进行垂直迭代计算,该过程称之为BEEPSHorizontalVertical。然后再对原始图像数据先进行垂直方向的迭代计算,在对该结果进行垂直方向的迭代计算,该过程称之为BEEPSVerticalHorizontal。最后的图像结果为(BEEPSHorizontalVertical+BEEPSVerticalHorizontal)/2;
比如上述公式1中最后体现在代码中可能如下(progressive):
for (int k = startIndex + 1, K = startIndex + length;(k < K); k++)
{
mu = data[k] - rho * data[k - 1];
mu = spatialContraDecay * exp(c * mu * mu);
data[k] = data[k - 1] * mu + data[k] * (1.0 - mu) / rho;
}式3的代码可能为(regressive):
for (int k = startIndex + length - 2; (startIndex <= k); k--)
{
mu = data[k] - rho * data[k + 1];
mu = spatialContraDecay * exp(c * mu * mu);
data[k] = data[k + 1] * mu + data[k] * (1.0 - mu) / rho;
}具体的代码可以从上述提供的相关网页里寻找,或者直接从这里下载。
话说JAVA的源码要修改成C#的,那简直就是很爽啊,有些复制过来基本都不要改动的。
这个算法特别适合于并行计算。
使用这个滤镜的过程就会发现,他对边缘的保护很好,而对一些变化平坦的区域总是会其更加平滑,总体感觉和表面模糊很像(表面模糊其实也是一种双边滤波器),以前曾考虑过用表面模糊来实现磨皮,但是由于目前所知道的表面模糊的任何优化算法都还是比较慢(但效果和PS是完全一致的),因此一直没有真正实践,这次看到这篇论文,经过我的实践,如果参数取的适当,如在和肤色检测或其他方式配合,完全可以实现较好的自动磨皮效果。
比如,针对一些图像,我做了如下测试和比较:
原 图 本文 λ=0.02,photometricStandardDeviation =10
美图秀秀智能磨皮,参数为深 可牛影像超级磨皮
和美图秀秀的比较,似乎看不出有什么区别,而可牛的明显的有不少瑕疵。
再做一些比较:
原 图 本文 λ=0.02,photometricStandardDeviation =10
美图秀秀智能磨皮,参数为深 可牛影像超级磨皮
再来一副:
原图 本文 美图 可牛
无论是那一副图,似乎可牛的效果总会硕一些,有颗粒感。
在看看一些皮肤严重粗糙的图片的效果:
原 图 本文 λ=0.02,photometricStandardDeviation =20
美图秀秀智能磨皮,参数为深 可牛影像超级磨皮
本文通过适当的调整参数,是的皮肤部位的磨皮效果比美图秀秀和可牛要好,但是头发部位的信息有所丢失。
从上面这副图中,可以看出,可牛的算法在最下部产生了一条黑线,这明显是可牛在算法层面上有BUG所致。国内的软件这些细节方面注意的不到位啊。
在http://www.cnblogs.com/celerychen/archive/2013/03/09/2951581.html的博客中,他的算法对上面这幅获得更好的效果,但他对使用的算法没有提到。
上述所有的图像都是直接拿这个双指数边缘保留平滑滤波实现的,未使用任何其他的辅助的技术。
当然,美图这些软件应该还是更专业些,我这里举得例子可能都是找了一些对我这个有利的来说明的,但无论如何,这种边缘保留特性的滤波器作为磨皮的一种辅助手段是必然有其生存空间的。
习惯性动作,提供一个可供大家测试效果的程序: 基于双指数边缘保留平滑器的磨皮测试
无论文章写得好不好,都希望能获得各位看客的支持,有的时候一个小点击或小回复也是给作者继续写作的动力源泉。
*********************************作者: laviewpbt 时间: 2013.8.31 联系QQ: 33184777 转载请保留本行信息************************