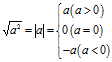16.1（1）二次根式
教学重点
导出
有意义的条件，掌握性质1,2
教学过程
复习：
正数
的平方根是
，零的平方根是零，负数没有平方根。
既然负数没有平方根，所以
中，被开方数
是非负数。
板书：
代数式
（
）叫做二次根式。读作"根号
"。
性质1：
例：设
是实数，当
满足什么条件时，下列各式有意义
本例重点强调一元一次不等式的计算，特别是移项，系数化一。
学生练习：填写教材P3表格，引出性质1
性质1：
性质2：
例：求值
，其中
本例免去学生正负判断推理的书写过程
作业：练习册
教学反思
1.将教材性质1略作改动，改为
，培养学生去根号后加绝对值和分类讨论的习惯。
16.1（2）二次根式
教学重点
将被开方数是单项式或分式的二次根式化简
教学过程
板书：
性质3：
，其中
，
性质4：
，其中
，
例：化简二次根式（复习分解素因数）
本例教师后方演示短除法分解素因数，并要求学生作业本上必须有此草稿。
例：化简二次根式
解：
问：本例和前两例的被开方数有什么不同？（被开方数由数字变成字母）
问：
是否正确？什么情况下是（不）正确的？
因为字母不像数字，有正负零三种可能，因此需要考虑字母为负数的可能性。
例：化简二次根式
（
）
问：假如题目没有给出
这个条件，你怎么办？
例：化简二次根式
（
）
问：
分子分母都乘以
，方便不方便？
本例强调先分解再给分母"配对"的思想，以免给计算带来不便。
作业：练习册
教学反思
1. 化简
，原则上分子分母都乘以
后，以分数线为界"大根号拆成小根号"，需要有一步判断两个被开方数会不会是负数的过程，才能决定是否能用性质4，但是对于部分差生，在做此类计算题可以弱化这一步，直接使用性质4，确保计算题可以解出。
2.本节课问题较多，教师不应吝啬课堂时间，多提问，让学生有机会举手发言。
16.2（1）最简二次根式和同类二次根式
教学重点
判别最简二次根式，将被开方数是多项式或分式的二次根式，先因式分解，再化简。
教学过程
分析：
，
，
（
）
板书：
被开方数同时满足以下两个条件的二次根式，叫做最简二次根式
1.被开方数中各因式的指数都为1
2.被开方数不含分母
例：判断最简二次根式
本例需要复习平方差公式，完全平方公式。同时一边判断，一边指导学生化简。
例：化成最简二次根式
（
） 
，其中
，其中
问：为什么题目规定
？没有这个条件可不可以？
作业：练习册
教学反思
1.本节课与上一节课的不同点在于新增了先分解因式，再化简的步骤，对于部分优秀生，可以另补充此类题目。
16.2（2）最简二次根式和同类二次根式
教学重点
会判别几个二次根式是同类二次根式，合并同类二次根式
教学过程
化简：
，
观察发现，以上两个最简二次根式中，被开方数相同，我们称之为同类二次根式。
板书：
几个二次根式化成最简二次根式后，如果被开方数相同，那么这几个二次根式叫做同类二次根式。
例：找出同类二次根式
注意：先提醒学生，找之前先化简
（
） 
（
）
在后三个二次根式化简上，一定要培养学生加绝对值再判断的习惯。
有时候长得"像"的两个二次根式不一定是同类二次根式，反之亦然。所以一定要先化简成最简二次根式，然后才能判断。
例：合并同类二次根式
先复习乘法分配律
作业：练习册
教学反思
1.本节合并同类二次根式对学生来说掌握难度很低，只需复习乘法分配律，用少量时间即可。
2.重点是同类二次根式的判别，但难度依旧在化简上，所以时间还是多花在化简的练习上，因此本节课是一节略带新知识点的复习课。
16.3（1）二次根式的运算（加法和减法）
教学重点
熟练解决常数项含二次根式的一次方程和一次不等式
教学过程
作业分析：合并同类二次根式
提问：我们目前遇到的题目中，都是同类二次根式加减法，我们只需要进行简单的合并即可。如果我们遇到的二次根式难以一眼看出是不是同类二次根式，甚至根本不是同类二次根式，我们该怎么办？
例：
答案：
例：
答案：
小结：不是同类二次根式，是不可以做加减法的
例：
答案：
例：
答案：
例：解不等式
答案：
，最后要写结论
练习：教材P12
作业：练习册
教学反思
1.合并同类二次根式上节课已经完成目标，所以本节课的时间重点花在需要化简才能加减的二次根式运算上，特别是一元一次不等式的解法需要重点补充。
16.3（2）二次根式的运算（乘法和除法）
教学重点
掌握二次根式的性质3,4，掌握乘除运算的法则
教学过程
复习性质3,4
，其中
，
，同样的，我们得到
，其中
，
，同样的，我们得到
，
，
，
例：
问：
，这个绝对值有没有办法去除？哪个地方已经提示我们
是非负数？
例：
（
）
总结：先"小根号变大根号"，再化简，最后"分母配对去根号"
作业：练习册
教学反思
1.教材上有"两个二次根式相乘，被开方数相乘，根指数不变"等文字表述，但是课上可以不板书，而采用字母表示更直观。教师可以趁此机会把根指数的定义说一下。
2.本节课对上学年单项式乘法运算关联度很高，因此课上重点花时间复习该部分内容
16.3（3）二次根式的运算（分母有理化）
教学重点
利用分母有理化进行除式为一个根式的除法运算，以及考查分母有理化的解方程和解不等式
教学过程
计算
分析：先把除式化成分式的形式：
然后，学生的解题方法开始发生分歧。第一种是采用性质4，把两个小根号合并成一个大根号，然后，前提是被开方数都是非负数，如：
第二种，部分学生在已经预习，或者通过独立思维，觉得利用分式的基本性质，分子分母同时乘以一个不为零的代数式，如：
学生体验后发觉，第二种方法也能达成把分母去根号的目的，引出分母有理化这个方法。
黑板板书（左）：
把分母中的根号化去，叫做分母有理化。分母有理化的方法，一般是把分子和分母都乘以同一个适当的代数式，使得分母不含根号。
讲解：
"适当的"说明分母有理化时，乘以的代数式不一定是分母本身，具体我们看题目。
例：
分析：
这一步，大多数学生都可以完成。之后，学生的做法发生了分歧。
第一种，分子分母同时乘以
，这类学生的想法是"先把分母去根号再说"，但紧接着是遇到
需要化简的问题，有些学生甚至没有化简就结束解题。
第二种，把
，通过分母的化简，我们发现分子分母乘以
，比乘以
来得更加简便，至少省去了约分这一环节。
第三种，
，分子分母同乘
，解题完毕。
教师总结：第一种解法不推荐，因为在没有化简的基础上就先进行分母有理化，导致后期工作，如化简，再约分，更加复杂。第二种解法推荐，先化简，再分母有理化。第三种方法予以表扬，但不是通用的方法。
例：
例：
，其中
练习：教材P16
作业：练习册
教学反思
1.本节课，重点在挑选最佳的代数式来完成分母有理化，在完成分母有理化这个大目标后，课堂剩下的时间重点完成解方程和不等式两部分的计算训练。
16.3（4）二次根式的运算（混合运算）
教学重点
掌握有理化因式，以及和有理化因式有关的代数式求值和一元一次不等式
教学过程
复习：
，
计算：
，
复习分母有理化
把分母中的根号化去，叫做分母有理化。分母有理化的方法，一般是把分子和分母都乘以同一个适当的代数式，使得分母不含根号。
引例：
问：分子分母乘以什么合适？
因为
，所以这个
这个代数式最合适。
板书：
两个含有二次根式的非零代数式相乘，如果它们的积不含有二次根式，我们称这两个含有二次根式的非零代数式互为有理化因式。
例如：
和
，
和
有理化因式不唯一，例如
和
例：
问：
的有理化因式是什么？
例：
（
）
此题有两种解法，多花时间启发学生思维。
通用做法：
，引导学生思考为什么
简便做法：
计算：
最后结果要化成分式形式
问：此题可否用性质4拆掉大根号？
例：已知
，求
的值
注意：先化简，再代入
例：解不等式
注意：不要有
是正数的错觉
作业：练习册
教学反思
1.本节课时间非常紧，不得不占用其他时间来完成教学目标。主要是引例上，不少学生认为
分子分母乘以
也是可以分母有理化的，所以花了时间让学生去尝试体验，发觉分母越乘越复杂后，得出应该乘以
这个代数式最合适。
2. 
（
）这道题，部分聪明的学生能够想出第二种做法，但是第一种通用的做法，还是必须要讲的。