连连看游戏设计
连连看是一种很受大家欢迎的小游戏。微软亚洲研究院的实习生们就曾经开发过一个类似的游戏--Microsoft Link-up。
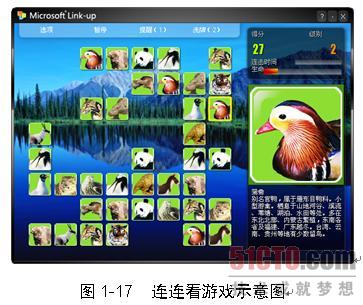 |
图1-17为Microsoft Link-up的一个截图。如果用户可以把两个同样的图用线(连线拐的弯不能多于两个)连到一起,那么这两个头像就会消掉,当所有的头像全部消掉的时候,游戏成功结束。游戏头像有珍稀动物、京剧脸谱等。Microsoft Link-up还支持用户输入的图像库,微软的同事们曾经把新员工的漫画头像加到这个游戏中,让大家在游戏之余也互相熟悉起来。
假如让你来设计一个连连看游戏的算法,你会怎么做呢?要求说明:
1. 怎样用简单的计算机模型来描述这个问题?
2. 怎样判断两个图形能否相消?
3. 怎样求出相同图形之间的最短路径(转弯数最少,路径经过的格子数目最少)。
4. 怎样确定目前是处于死锁状态,如何设计算法来解除死锁?
分析与解法
连连看游戏的设计,最主要包含游戏局面的状态描述,以及游戏规则的描述。而游戏规则的描述就对应着状态的合法转移(在某一个状态,有哪些操作是满足规则的,经过这些满足规则的操作,会到达哪些状态)。所以,自动机模型适合用来描述游戏设计。
下面是一个参考的连连看游戏的伪代码:
代码清单1-22
- 生成游戏初始局面
- Grid preClick = NULL, curClick = NULL;
- while(游戏没有结束)
- {
- 监听用户动作
- if(用户点击格子(x, y),且格子(x, y)为非空格子)
- {
- preClick = curClick;
- curClick.Pos = (x, y);
- }
- if(preClick != NULL && curClick != NULL
- && preClick.Pic == curClick.Pic
- && FindPath(preClick, curClick) != NULL)
- {
- 显示两个格子之间的消去路径
- 消去格子preClick, curClick;
- preClick = curClick = NULL;
- }
- }
从上面的整体框架可以看到,完成连连看游戏需要解决下面几个问题:
 |
1. 生成游戏初始局面。
2. 每次用户选择两个图形,如果图形满足一定条件(两个图形一样,且这两个图形之间存在少于3个弯的路径),则两个图形都能消掉。给定具有相同图形的任意两个格子,我们需要寻找这两个格子之间在转弯最少的情况下,经过格子数目最少的路径。如果这个最优路径的转弯数目少于3,则这两个格子可以消去。
3. 判断游戏是否结束。如果所有图形全部消去,游戏结束。
4. 判断死锁,当游戏玩家不可能再消去任意两个图像的时候,游戏进入"死锁"状态。如图1-18,该局面中已经不存在两个相同的图片相连的路径转弯数目小于3的情况。
在死锁的情况下,我们也可以暂时不终止游戏,而是随机打乱局面,打破"死锁"局面。
首先思考问题:怎样判断两个图形能否相消?在前面的分析中,我们已经知道,两个图形能够相消的充分必要条件是这两个图形相同,且它们之间存在转弯数目小于3的路径。因此,需要解决的主要问题是,怎样求出相同图形之间的最短路径。首先需要保证最短路径的转弯数目最少。在转弯数目最少的情况下,经过的格子数目也要尽可能地少。
在经典的最短路径问题中,需要求出经过格子数目最少的路径。而这里,为了保证转弯数目最少,需要把最短路径问题的目标函数修改为从一个点到另一个点的转弯次数。虽然目标函数修改了,但算法的框架仍然可以保持不变。广度优先搜索是解决经典最短路问题的一个思路。我们看看在新的目标函数(转弯数目最少)下,如何用广度优先搜索来解决图形A(x1, y1)和图形B(x2, y2)之间的最短路径问题。
首先把图形A(x1, y1)压入队列。
然后扩展图形A(x1, y1)可以直线到达的格子(即图形A(x1, y1)可以通过转弯数目为0的路径(直线)到达这些格子)。假设这些格子为集合S0,S0 = Find(x1, y1)。如果图形B(x2, y2)在集合S0中,则结束搜索,图形A和B可以用直线连接。
否则,对于所有S0集合中的空格子(没有图形),分别找到它们可以直线到达的格子。假设这个集合为S1。S1 = {Find(p)| p ∈S0}。S1包含了S0,我们令S1'= S1-S0,则S1'中的格子和图形A(x1, y1)可以通过转弯数目为1的路径连起来。如果图形B(x2, y2)在S1'中,则图形A和B可以用转弯数目为1的路径连接,结束搜索。
否则,我们继续对所有S1'集合中的空格子(没有图形),分别找出它们可以直线到达的格子,假设这个集合为S2,S2 = Find{ Find(p)| p ∈S1'}。S2包含了S0和S1,我们令S2'= S2 - S0 - S1 = S2 - S0 - S1'。集合S2'是图形A(x1, y1)可以通过转弯数目为2的路径到达的格子。如果图形B(x2, y2)在集合S2'中,则图形A和B可以用转弯数目为2的路径连接,否则图形A和B不能通过转弯小于3的路径连接。
在扩展的过程中,只要记下每个格子是从哪个格子连过来的(也就是转弯的位置),最后图形A和B之间的路径就可以绘制出来。
在上面的广度优先搜索过程中,有两步操作:S1' = S1 - S0和S2'= S2 - S0 -S1。它们可以通过记录从图形A(x1, y1)到该格子(x, y)的转弯数目来实现。开始,将所有格子(x, y)和格子A(x1, y1)之间路径的最少转弯数目MinCrossing(x, y)初始化为无穷大。然后,令MinCrossing(A)= MinCrossing(x1, y1)= 0,格子A到自身当然不需要任何转弯。第一步扩展之后,所有S0集合中的格子的MinCrossing值为0。在S0集合继续扩展得到的S1集合中,格子X和格子A之间至少有转弯为1的路径,如果格子X本身已经在S0中,那么,MinCrossing(X)= 0。这时,我们保留转弯数目少的路径,也就是MinCrossing(X)= MinValue(MinCrossing(X), 1)= 0。这个过程,就实现了上面伪代码中的S1'= S1 - S0。S2'= S2 - S0-S1的扩展过程也类似。
经过上面的分析,我们知道,每一个格子X(x, y),都有一个状态值MinCrossing(X)。它记录下了该格子和起始格子A之间的最优路径的转弯数目。广度优先搜索,就是每次优先扩展状态值最少的格子。如果要保证在转弯数目最少的情况下,还要保持路径长度尽可能地短,则需要对每一个格子X保存两个状态值MinCrossing(X)和MinDistance(X)。从格子X扩展到格子Y的过程,可以用下面的伪代码实现:
- if((MinCrossing(X) + 1 < MinCrossing(Y)) ||
- ((MinCrossing(X) + 1 == MinCrossing(Y) &&
- (MinDistance(X) + Dist(X,Y) < MinDistance(Y)))
- {
- MinCrossing(Y) = MinCrossing(X) + 1;
- MinDistance(Y) = MinDistance(X) + Dist(X, Y);
- }
也就是说,如果发现从格子X过来的路径改进了转弯数目或者路径的长度,则更新格子Y。
"死锁"问题本质上还是判断两个格子是否可以消去的问题。最直接的方法就是,对于游戏中尚未消去的格子,都两两计算一下它们是否可以消去。此外,从上面的广度优先搜索可以看出,我们每次都是扩展出起始格子A(x1, y1)能够到达的格子。也就是说,对于每一个格子,可以调用一次上面的扩展过程,得到所有可以到达的格子,如果这些格子中有任意一个格子的图形跟起始格子一致,则它们可以消去,目前游戏还不是"死锁"状态。
扩展问题:
1. 在连连看游戏设计中,是否可以通过维护任意两个格子之间的最短路径来实现快速搜索?在每一次消去两个格子之后,更新我们需要维护的数据(任意两个格子之间的最短路径)。这样的思路有哪些优缺点,如何实现呢?
2. 在围棋或象棋游戏中,经过若干步操作之后,可能出现一个曾经出现过的状态(例如,围棋中的打劫)。如何在围棋、象棋游戏设计中检测这个状态呢?