利用Python通过频谱分析和KNN完成iphone拨号的语音识别

最近这段时间，学校里的事情实在太多了，从七月下旬一直到八月底实验室里基本天天十二点或者通宵，实在是没有精力和时间来写博客。这周老师出国开会，也算有了一个短暂的休息机会，刚好写点有意思的东西。

上周在天津的会议上碰到一个北交的姐们儿，她想利用小波变换来处理失超信号，刚好之前自己就有这个想法，所以回来后就想着把相关的内容好好复习复习，最相关的就是傅里叶分析和小波变换了。数学推导固然重要，但写那个实在是太乏味了，然后想到之前网上一个新闻，说一个同学通过新闻里记者拨号的声音反推出了周鸿祎的手机号码，就想着能不能自己也做一个这样的号码识别程序呢？

说做就做，首先整理一下思路，我觉得大概的流程应该包括一下几步：

1 单键声音的采集与分析

这是后面号码识别的基础，针对每个按键音分析其在频域上的分布规律进而得到一个基准，后面再采集到的声音可据此进行判定。

2 声音的降噪

自己录的这些声音总不会太完美，直接进行频谱分析，会得到一个非常杂乱的结果，所以有效的声音降噪可以帮助我们更加精确地进行判断。

3 号码识别思路

我想的方案主要是两种，刚好也符合我最近复习的这两种变换

A 对声音文件进行有效区域划分，然后对每个区域单独进行频谱分析，然后比对训练数据，推断每一处对应的号码，最后输出。

B 采用小波分析，输出对应声音文件的小波时频图，观察其在不同时刻频域各处强度的变化，进而确定所拨的号码。

两种方案我感觉应该都可以，不过第一种感觉相对要简单一点，所以我们就先来试试第一个。

Ok，那第一步我们得先找到合适的单个按键音数据，这个上网一搜iphone按键音就找到了，下载下来发现刚好又是wav文件，可以用Python自带的wave库直接处理，简直美滋滋。

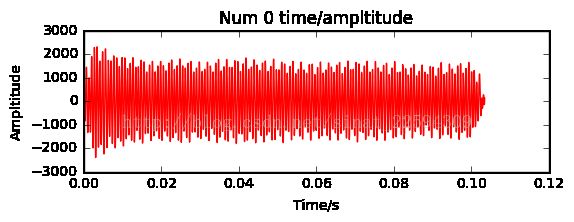
简单说一下wave库，用它读取一个wave文件后，我们可以获取四个参数，包括通道数目，样本宽度，采样率以及采样数目。根据通道数目，你可以确定是单通道和双通道，如果是单通道你直接读取采样文件就行，但如果是双通道，采样是一左一右轮着来的，所以到时候你还得把它分成两列，然后选择其中一列来读。从网上下载的这些音源刚好是单声道的，所以直接读取就行了，下面以0为例，读取它的波形并画出来。

import numpy as np
import wave
from matplotlib import pyplot as plt
file_path='C:\Users\**\Desktop\iphone\dtmf-0.wav'
f=wave.open(file_path,'rb')
num=file_path[-5] 
params=f.getparams()
nchannels,samplewidth,framerate,nframes=params[:4]
str_data=f.readframes(nframes)
f.close()
wave_data=np.fromstring(str_data,dtype=np.short)
wave_data.shape=-1,1
if nchannels==2:
    wave_data.shape=-1,2
else:
    pass
wave_data=wave_data.T
time=np.arange(0,nframes)*(1.0/framerate)
plt.subplot(211)
plt.plot(time,wave_data[0],'r-')
plt.xlabel('Time/s')
plt.ylabel('Ampltitude')
plt.title('Num '+num+' time/ampltitude')
plt.show()

结果如下

其实波形看起来还是比较规律的，但明显是有不同频率的波叠加在一起，所以下一步我们采用傅里叶分析，看看它在频域上是什么样的。Python中进行傅里叶分析是十分方便的，直接利用numpy中的fft就行，分解完成后，考虑到高频的成分不需要，所以选择4000做个阈值，超出这个区域的都舍掉。另外，因为目前我并不考虑信号的重构，所以我直接把对应频率的幅值去了绝对值，这样方便我下一步寻找波峰。完成这些操作后，画个频谱图看看有什么规律。

df=framerate/(nframes-1)
freq=[df*n for n in range(0,nframes)]
transformed=np.fft.fft(wave_data[0])
d=int(len(transformed)/2)
while freq[d]>4000:
    d-=10
freq=freq[:d]
transformed=transformed[:d]
for i,data in enumerate(transformed):
    transformed[i]=abs(data)
plt.subplot(212)
plt.plot(freq,transformed,'b-')
plt.xlabel('Freq/Hz')
plt.ylabel('Ampltitude')
plt.title('Num '+num+' freq/ampltitude')
plt.show()

结果如下

哎呀我去，这也太完美了吧……我都怀疑下的这些波形文件是电脑写的，也太规整了，仅在两个频率处出现了峰值，其余处为0，感觉事情并不简单，上网查了一圈发现Iphone的按键音采用的是DTMF，双音多频，每个按键音都是一个高频加一个低频信号的叠加。原来如此，那我就放心继续做下去了。那么下一步是提取这两个频率值，上面我已经说了，为了方便我寻找这两个波峰，我已经将平率对应幅度全部取绝对值，现在其实就是找到两个局部极值对应的频率就好。那首先找到两个极大值，然后确定它们的位置再对应到频域上就OK，代码如下

local_max=[]
for i in np.arange(1,len(transformed)-1):
    if transformed[i]>transformed[i-1] and transformed[i]>transformed[i+1]:
        local_max.append(transformed[i])
local_max=sorted(local_max)
loc1=np.where(transformed==local_max[-1])
max_freq=freq[loc1[0][0]]
loc1=np.where(transformed==local_max[-2])
min_freq=freq[loc1[0][0]]
print 'Two freq ',max_freq,min_freq

结果如下

Two freq  1278 900

好的，针对一个数字的音频分析完成了，那其他的数字也如法炮制，定义一个函数，再用个循环就好，最后把这些数字所对应的频率画在图上，整体代码如下：

import wave
import numpy as np
from matplotlib import pyplot as plt

def wave_analysis(file_path):
    f=wave.open(file_path,'rb')
    num=file_path[-5] 
    params=f.getparams()
    nchannels,samplewidth,framerate,nframes=params[:4]
    str_data=f.readframes(nframes)
    f.close()
    wave_data=np.fromstring(str_data,dtype=np.short)
    wave_data.shape=-1,1
    if nchannels==2:
        wave_data.shape=-1,2
    else:
        pass
    wave_data=wave_data.T
    time=np.arange(0,nframes)*(1.0/framerate)
    plt.subplot(211)
    plt.plot(time,wave_data[0],'r-')
    plt.xlabel('Time/s')
    plt.ylabel('Ampltitude')
    plt.title('Num '+num+' time/ampltitude')
    plt.show()
    df=framerate/(nframes-1)
    freq=[df*n for n in range(0,nframes)]
    transformed=np.fft.fft(wave_data[0])
    d=int(len(transformed)/2)
    while freq[d]>4000:
        d-=10
    freq=freq[:d]
    transformed=transformed[:d]
    for i,data in enumerate(transformed):
        transformed[i]=abs(data)
    plt.subplot(212)
    plt.plot(freq,transformed,'b-')
    plt.xlabel('Freq/Hz')
    plt.ylabel('Ampltitude')
    plt.title('Num '+num+' freq/ampltitude')
    local_max=[]
    for i in np.arange(1,len(transformed)-1):
        if transformed[i]>transformed[i-1] and transformed[i]>transformed[i+1]:
            local_max.append(transformed[i])
    local_max=sorted(local_max)
    loc1=np.where(transformed==local_max[-1])
    max_freq=freq[loc1[0][0]]
    loc1=np.where(transformed==local_max[-2])
    min_freq=freq[loc1[0][0]]
    plt.show()
    print 'Two freq ',max_freq,min_freq
    return max_freq,min_freq
    

def main():
    x=[]
    y=[]
    for i in np.arange(0,10):
        path='C:\Users\**\Desktop\iphone\dtmf-'+str(i)+'.wav'
        max_freq,min_freq=wave_analysis(path)
        x.append(i)
        y.append(max_freq)
        x.append(i)
        y.append(min_freq)
    plt.scatter(x,y,marker='*')
    plt.show()

if __name__=='__main__':
    main()

中间的振幅和频域的图就不贴了，就看一下最后一张每个数字所对应的特定频率图

把数字填到表格里是这样

0	1	2	3	4	5	6	7	8	9
900	640	649	664	744	711	686	784	760	810
1278	1110	1243	1408	1168	1233	1316	1112	1192	1404

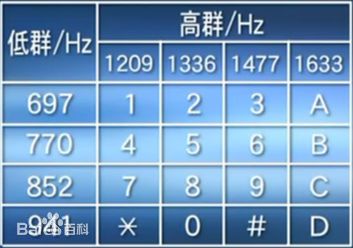
其实规律还是很容易看出来的，每个按键音对应于一个高频和一个低频，其中，123,456,789的低频部分相似，147,258,369的高频部分相似，这和DTMF是一致的，从百科上扒了一张图，大家可以对比一下

展现出来的规律是相似的，但数值并不完全一样，我们计算出来的似乎有那么一点点偏小，但这并不重要，赶紧拿个实际录音来看看吧。

先录了10个单音，看看频谱分析怎么样，完全同样的方法，针对数字0，结果如下

Two freq  1283 1270

发现问题了没

1 录音的数据并不是全程都是按键音，很大一部分是无用的，整体进行傅里叶分析会产生非常大的干扰信号

2 录音的数据里叠加有很多噪声，导致频域分布复杂。

3 频域信号里有很多的毛刺，这样导致产生了很多局部极大值，导致我们之前用的寻找波峰的算法失效。

OKOK，那我们一步步来解决问题。

首先第一个相当于就是有效波形的提取了。高级的方法我也不会啊，但就直观来看，明显有效区域的波形幅度远大于无效区，那我们是不是可以取个阈值，从第一个超过该阈值的开始记为起始点，然后连续超过多少个点都小于阈值后记为终止点，当然可以，在这里我选择的阈值是最大值的5%，事实表明这样还是很有效的。

那对与第二个问题，其实噪声很多都是高频的，首先滤除高频部分是一个选项，其次即使是噪声，它往往也是周期性的，一个周期内的噪声叠加起来往往为0，所以我们选一个时间窗口，进行移动平均，这样可以有效的消除噪声的影响。同时，这也能解决第三步遇到的问题，移动平均最大的好处就是会使曲线变得光滑，不会出现很多的毛刺，这样通过移动平均处理后的频域图又可以重新使用我们之前所说的寻找局部极值来确定频率的方法。哦，对了对了，移动平均可以通过卷积操作来实现，非常简单。代码如下

import wave
import numpy as np
from matplotlib import pyplot as plt
#load wave file and get params
file_path='C:\\Users\\**\\Desktop\\iphone\\Test\\0.wav'
f=wave.open(file_path,'rb')
#num=file_path[-5] 
num=str(0)
params=f.getparams()
nchannels,samplewidth,framerate,nframes=params[:4]
str_data=f.readframes(nframes)
f.close()
wave_data=np.fromstring(str_data,dtype=np.short)
wave_data.shape=-1,1
if nchannels==2:
    wave_data.shape=-1,2
else:
    pass
wave_data=wave_data.T
#moving average
def moving_average(data,n):
    weights=np.ones(n)
    weights/=weights.sum()
    ma=np.convolve(data,weights,mode='full')[:len(data)]
    ma[:n]=ma[n]
    return ma

new_data=moving_average(wave_data[0],10)
new_data=moving_average(new_data,10)
new_data_2=[]
max_wave=new_data.max()
#look for the start point and end point
index=0
flag=False
for i in np.arange(0,len(new_data)):
#    index=0
    if abs(new_data[i])>=0.05*max_wave:
        new_data_2.append(new_data[i])
        index=0
        if abs(new_data[i+1])<0.05*max_wave:
            for j in np.arange(1,40):
                if abs(new_data[i+1+j])<0.05*max_wave:
                    index+=1
                    if index>=39:
                        print index 
                        flag=True
                        break
    if flag==True:
        break
                

time=np.arange(0,len(new_data_2))*(1.0/framerate)
plt.subplot(211)
plt.plot(time,new_data_2,'r-')
plt.xlabel('Time/s')
plt.ylabel('Ampltitude')
plt.title('Num '+num+' time/ampltitude')
plt.show()
df=framerate/(len(new_data_2)-1)
freq=[df*n for n in range(0,len(new_data_2))]
transformed=np.fft.fft(new_data_2)
d=int(len(transformed)/2)
while freq[d]>2000:
    d-=10
freq=freq[:d]
transformed=transformed[:d]
for i,data in enumerate(transformed):
    transformed[i]=abs(data)
transformed=moving_average(transformed,5)
transformed=moving_average(transformed,5)
transformed=moving_average(transformed,5)    
plt.subplot(212)
plt.plot(freq,transformed,'b-')
plt.xlabel('Freq/Hz')
plt.ylabel('Ampltitude')
plt.title('Num '+num+' freq/ampltitude')
plt.show()
#look for local maximum
local_max=[]
for i in np.arange(1,len(transformed)-1):
    if transformed[i]>transformed[i-1] and transformed[i]>transformed[i+1]:
        local_max.append(transformed[i])
local_max=sorted(local_max)
loc1=np.where(transformed==local_max[-1])
freq1=freq[loc1[0][0]]
loc1=np.where(transformed==local_max[-2])
freq2=freq[loc1[0][0]]
    
            
print 'Two freq ',freq1,freq2

结果如下

Two freq  1368 981

蛤蛤蛤，perfect！！！有效信号的提取以及频谱分析都没有问题了，唯一的遗憾就是分解出来的两个频率值又和之前下载的版本不一致了，不过没关系，我们还是要相信实际结果。接下来依次对录的其他号码进行分析，得到新的各个号码对应两个频率值。

得到了所有号码对应的两个频率值之后，我们就可以对再采集的信号进行预测了。采用什么预测方法呢？在之前博客里写过很多很多分类方法，但我觉得都不用，为啥呢，训练数据太少了，算法再高级也没卵用，哎呀，好丧啊……那我们就用最朴素的方法吧，计算采样数据的两个频率与所有训练数据频率的距离，选择最小的那个作为输出，当然你也可以宣称用的是KNN算法，没毛病啊，就是最近邻呀……

回到最开始说的，我们想做的是一个语音号码识别，所以这里还要考虑一段数据包含多个按键音的有效区域提取，因为之前的算法时针对单音的。一开始我以为只要把之前的跳出循环操作改成保存数据，标记置0就OK，后来发现我实在是天真了，这样做的后果就是除了我们真实有效区域以外，偶尔有一个噪声超过阈值的也全都提取出来了。所以除了幅度阈值之外，我对提取的有效区域长度也做了一个限制，进而保提取的区域都是我们的目标区域。

至此，全部的问题都解决了，整合一下代码，最终如下

import wave
import numpy as np
from matplotlib import pyplot as plt

#moving average
def moving_average(data,n):
    weights=np.ones(n)
    weights/=weights.sum()
    ma=np.convolve(data,weights,mode='full')[:len(data)]
    ma[:n]=ma[n]
    return ma


        
#get wave data
def get_wave_data(file_path):
    f=wave.open(file_path,'rb')
    params=f.getparams()
    nchannels,samplewidth,framerate,nframes=params[:4]
    str_data=f.readframes(nframes)
    f.close()
    wave_data=np.fromstring(str_data,dtype=np.short)
    wave_data.shape=-1,1
    if nchannels==2:
        wave_data.shape=-1,2
    else:
        pass
    wave_data=wave_data.T
    return wave_data[0],framerate

#find the efficient area in wave
def find_efficient_area(wave_data):
    wave_data=moving_average(wave_data,10)
    wave_data=moving_average(wave_data,10)
    wave_data=moving_average(wave_data,10)
    wave_data=moving_average(wave_data,10)
    new_data=[]
    max_wave=wave_data.max()
    efficient_data=[]
    index=0
    count=0
    flag=False
    for i in np.arange(0,len(wave_data)):
        if abs(wave_data[i])>=0.05*max_wave:
            new_data.append(wave_data[i])
            index=0
            if i+1>=len(wave_data):
                break
            if abs(wave_data[i+1])<0.05*max_wave:
                for j in np.arange(1,60):
                    if i+1+j>=len(wave_data):
                        break
                    if abs(wave_data[i+1+j])<0.05*max_wave:
                        index+=1
                if index>=59: 
                    flag=True
                        
                
              
        if flag==True:
            if len(new_data)>2000:
#                plt.plot(new_data,'r-')
#                plt.show()
                efficient_data.append(new_data)
                count+=1
            new_data=[]
            index=0
            flag=False
    print 'Find ',count,' efficient wave'
    return efficient_data,count

#Analysis single wave data
def wave_analysis_single(efficient_data,framerate):
    time=np.arange(0,len(efficient_data[0]))*(1.0/framerate)
#    plt.plot(time,efficient_data[0],'r-')
#    plt.xlabel('Time/s')
#    plt.ylabel('Ampltitude')
#    plt.title(' time/ampltitude')
#    plt.show()
    df=framerate/(len(efficient_data[0])-1)
    freq=[df*n for n in range(0,len(efficient_data[0]))]
    transformed=np.fft.fft(efficient_data[0])
    d=int(len(transformed)/2)
    while freq[d]>2000:
        d-=10
    freq=freq[:d]
    transformed=transformed[:d]
    for i,data in enumerate(transformed):
        transformed[i]=abs(data)
    transformed=moving_average(transformed,5)
    transformed=moving_average(transformed,5)
    transformed=moving_average(transformed,5)
#    transformed=moving_average(transformed,5)
#    plt.plot(freq,transformed,'b-')
#    plt.xlabel('Freq/Hz')
#    plt.ylabel('Ampltitude')
#    plt.title(' freq/ampltitude')
#    plt.show()
    #look for local maximum
    local_max=[]
    for i in np.arange(1,len(transformed)-1):
        if transformed[i]>transformed[i-1] and transformed[i]>transformed[i+1]:
            local_max.append(transformed[i])
    local_max=sorted(local_max)
    loc1=np.where(transformed==local_max[-1])
    freq_1=freq[loc1[0][0]]
    loc1=np.where(transformed==local_max[-2])
    freq_2=freq[loc1[0][0]]
    print 'Frequency',freq_1,freq_2
    return freq_1,freq_2
        
        


#Get training data
train_data={}
for i in np.arange(0,10):
    file_path='C:\\Users\\**\\Desktop\\iphone\\Test\\'+str(i)+'.wav'
    wave_data,framerate=get_wave_data(file_path)
    data,count=find_efficient_area(wave_data)
    a,b=wave_analysis_single(data,framerate)
    train_data[i]=[a,b]



#multi_number estimate
def number_estimate(freq1,freq2):
    err=100000
    num=0
    for i in np.arange(0,10):
        tmp=(freq1-train_data[i][0])**2+(freq2-train_data[i][1])**2
        if tmp2000:
            d-=10
        freq=freq[:d]
        transformed=transformed[:d]
        for i,data in enumerate(transformed):
            transformed[i]=abs(data)
        transformed=moving_average(transformed,5)
        transformed=moving_average(transformed,5)   
        transformed=moving_average(transformed,5)
        plt.plot(freq,transformed,'b-')
        plt.xlabel('Freq/Hz')
        plt.ylabel('Ampltitude')
        plt.title(' freq/ampltitude')
        plt.show()
#        look for local maximum
        local_max=[]
        for i in np.arange(1,len(transformed)-1):
            if transformed[i]>transformed[i-1] and transformed[i]>transformed[i+1]:
                local_max.append(transformed[i])
        local_max=sorted(local_max)
        loc1=np.where(transformed==local_max[-1])
        freq_1=freq[loc1[0][0]]
        loc1=np.where(transformed==local_max[-2])
        freq_2=freq[loc1[0][0]]
        if freq_1

结果如下

[2, 2, 8, 1, 6, 1, 4, 3, 9, 9]

家里领导很肉麻地录的是5201314999，结果出来效果真的很垃圾啊……不过想想这训练数据这么少，并且采用了那么朴素的判定方法，正确率高了才见鬼了好吧！！！

不过人的智慧是无穷的，通过改变数据移动平均的次数以及一个小trick

#A little trick
train_data[1][0]=train_data[4][0]=train_data[7][0]=(train_data[1][0]+train_data[4][0]+train_data[7][0])/3

train_data[3][0]=train_data[6][0]=train_data[9][0]=(train_data[3][0]+train_data[6][0]+train_data[9][0])/3
train_data[1][1]=train_data[2][1]=train_data[3][1]=(train_data[1][1]+train_data[2][1]+train_data[3][1])/3

train_data[7][1]=train_data[8][1]=train_data[9][1]=(train_data[7][1]+train_data[8][1]+train_data[9][1])/3

train_data[2][0]=train_data[5][0]=train_data[8][0]=train_data[0][0]=(train_data[1][0]+train_data[3][0])/2
train_data[4][1]=train_data[5][1]=train_data[6][1]=(train_data[1][1]+train_data[7][1])/2

再次进行预测，结果为

[5, 2, 0, 1, 3, 1, 4, 9, 9, 9]

蛤蛤蛤，很厉害有没有？！

屁啦，没有普适性，对预测能力并没有质的提高，这个trick可以用，但是对数据进行移动平均的次数真的对预测结果有很大影响。

好啦，至此，我们第一个语音号码识别程序的demo已经出来了，虽然正确率只有60%左右，但这是个十分类问题啊喂，比你乱猜还是靠谱多了好吗！！！当然，提高的空间还很大，大家如果有兴趣的可以一起讨论讨论，比如我觉得可以对从频谱中得到的数据依照训练数据做个拉普拉斯平滑~

这周花了很多时间在这个小玩意儿上，课题的东西一点也没干，感觉周一组会老板回来要GoDie了，好慌啊，先歇个周六压压惊，周末愉快各位，蛤蛤蛤~~~