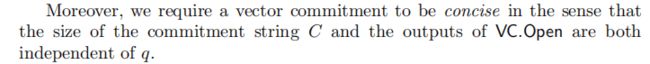Vector Commitments and their Applications学习笔记

1. 背景知识

Dario Catalano 和 Dario Fiore 2013年论文《Vector Commitments and their Applications》：
1）提出了a new non-interactive primitive——Vector Commitment（VC），指的是 commit to an ordered sequence of $q$ values $(m_1,\cdots ,m_q)$，除了具有普通commitment的binding和hiding特性外，还具有position binding特性：即可open commitment at specific positions——prove that $m_i$ is the $i$-th committed message，不存在open a commitment to two differenct values at the same position。

2）要求 Vector Commitment 应为concise简洁的：

• commitment string的size应与vector length $q$ 无关；
• opening的size也应与vector length $q$ 无关。

3）要求Vector Commitment updatable：

• 当 the $i$-th message 由 $m_i$ 变成 $m_i^{{}^{\prime }}$ 时，允许 committer 更新commitment值——由 $Com$ 更新为 $Co{m}^{{}^{\prime }}$ ，新的 $Co{m}^{{}^{\prime }}$ 中对应了更新后的 $m_i^{{}^{\prime }}$ 值；
• 当 the $i$-th message 由 $m_i$ 变成 $m_i^{{}^{\prime }}$ 时，允许 holders of an opening for a message at position $j$ w.r.t. $Com$ to update their proof so as to become valid w.r.t. the new $Co{m}^{{}^{\prime }}$。

4）提出了两种Vector Commitment实现：

• 基于RSA assumption的Vector Commitment实现；
• 基于Computational Diffie-Hellman (in bilinear groups) assumption的Vector Commitment实现。

5）指出了Vector Commitment的应用场景：

• Verifiable Databases with Efficient Updates；
• Updatable Zero-Knowledge Elementary Databases；
• Universal Dynamic Accumulators。

1.1 Trapdoor commitment schemes

又可称为chameleon commitment，若知晓trapdoor key，则可破坏commitment的binding属性，详细可看博客：

• 水银承诺mercurial commitment 。
• Almost Optimal Short Adaptive Non-Interactive Zero Knowledge学习笔记 第2.1节内容。

2. Vector Commitments

Vector Commitments 由如下基础算法组成：
1）VC.KeyGen($1,q$)：Given the security parameter $k$ and the size $q$ of the committed vector (with $q=poly(k)$), the key generation outputs some public parameters $pp$ (which implicitly define the message space $M$). 【生成Prover和Verifier的public info。】
2）VC.Com${}_{pp}$($m_1,\cdots ,m_q$)：On input a sequence of $q$ messages $m_1,\cdots ,m_q\in M$ and the public parameters $pp$, the committing algorithm outputs a commitment string $C$ and an auxiliary information $aux$. 【Prover生成commitment。】
3）VC.Open${}_{pp}$($m,i,aux$)：This algorithm is run by the committer to produce a proof ${\Lambda }_i$ that $m$ is the $i$-th committed message.【Prover生成proof。】
4）VC.Ver${}_{pp}$($C,m,i,{\Lambda }_i$)：The verification algorithm accepts (i.e., it outputs $1$) only if ${\Lambda }_i$ is a valid proof that $C$ was created to a sequence $m_1,\cdots ,m_q$ such that $m=m_i$.【Verifier验证proof。】
5）VC.Update${}_{pp}$($C,m,m^{{}^{\prime }},i$)：This algorithm is run by the committer who produced $C$ and wants to update it by changing the $i$-th message to $m^{{}^{\prime }}$. The algorithm takes as input the old message $m$, the new message $m^{{}^{\prime }}$ and the position $i$. It
outputs a new commitment $C^{{}^{\prime }}$ together with an update information $U$.【Prover更新commitment，为Verifier提供update information $U$。】
6）VC.ProofUpdate${}_{pp}$($C,{\Lambda }_j,m^{{}^{\prime }},i,U$)：This algorithm can be run by any user who holds a proof ${\Lambda }_j$ for some message at position $j$ w.r.t. $C$, and it allows the user to compute an updated proof ${\Lambda }_j^{{}^{\prime }}$ (and the updated commitment $C^{{}^{\prime }}$) such that ${\Lambda }_j^{{}^{\prime }}$ will be valid w.r.t. $C^{{}^{\prime }}$ which contains $m^{{}^{\prime }}$ as the new message at position $i$. Basically, the value $U$ contains the update information which is needed to compute such values.【利用update information $U$，Prover 或者 Verifier更新老的proof ${\Lambda }_j$为${\Lambda }_j^{{}^{\prime }}$。】

2.1 基于CDH的Vector Commitment实现

Square-CDH assumption：已知$g,g^a\in \mathbb{G}$，要计算$g^{a^2}$的值为computationally infeasible。
Square-CDH assumption与standard CDH assumption等价。

基于CDH assumption in bilinear groups，本文构建的Vector Commitment采用了 Bellare and Micciancio 1997年论文《A new paradigm for collision-free hashing: Incrementality at reduced cost》 中的incremental hash function思路：
1）VC.KeyGen($1^k,q$)：Let $\mathbb{G},{\mathbb{G}}_T$ be two bilinear groups of prime order $p$ equipped with a bilinear map $e:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_T$. Let $g\in G$ be a random generator. Randomly choose $z_1,\cdots ,z_q\leftarrow {\mathbb{Z}}_p$. For all $i=1,\cdots ,q$ set: $h_i=g^{z_i}$ . For all $i,j=1,\cdots ,q,i\ne j$ set $h_{i,j}=g^{z_i{z}_j}$ .
Set $pp=(g,\{h_i{\}}_{i\in [q]},\{h_{i,j}{\}}_{i,j\in [q],i\ne j})$. The message space is $M={\mathbb{Z}}_p$。【CRS的length为$\Theta (q^2)$，且$g^{z_i^2}$不在CRS中（需满足CDH assumption，$g^{z_i^2}$对Prover不可知）。】

2）VC.Com_{pp}($m_1,\cdots ,m_q$)：Compute $C=h_1^{m_1}{h}_2^{m_2}\cdots h_q^{m_q}={\prod }_{i=1}^q{h}_i^{m_i}$ and output $C$ and the auxiliary information $aux=(m_1,\cdots ,m_q)$。

3）VC.Open_{pp}($m_i,i,aux$)：Compute ${\Lambda }_i={\prod }_{j=1,j\ne i}^q{h}_{i,j}^{m_j}=({\prod }_{j=1,j\ne i}^q{h}_j^{m_j}{)}^{z_i}$。【生成proof的multi-exponentiation复杂度为$\Theta (q)$】

4）VC.Ver_{pp}($C,m_i,i,{\Lambda }_i$)：If $e(C/h_i^{m_i},h_i)=e({\Lambda }_i,g)$ then output $1$. Otherwise output $0$。

5）VC.Update_{pp}($C,m,m^{‘},i$)：Compute the updated commitment $C^{‘}=C\cdot h_i^{m^{‘}-m}$. Finally output $C^{‘}$ and $U=(m,m^{‘},i)$。

6）VC.ProofUpdate_{pp}($C,{\Lambda }_j,m^{‘},U$)：A client who owns a proof ${\Lambda }_j$, that is valid w.r.t. to $C$ for some message at position $j$, can use the update information $U=(m,m^{‘},i)$ to compute the updated commitment $C^{‘}$ and produce a new proof ${\Lambda }_j^{‘}$ which will be valid w.r.t. $C^{‘}$. We distinguish two cases：

• $i\ne j$：Compute the updated commitment $C^{‘}=C\cdot h_i^{m^{‘}-m}$ while the updated proof is ${\Lambda }_j^{‘}={\Lambda }_j\cdot (h_i^{m^{‘}-m}{)}^{z_j}={\Lambda }_j\cdot h_{j,i}^{m^{‘}-m}$。
• $i=j$：Compute the updated commitment as $C^{‘}=C\cdot h_i^{m^{‘}-m}$ while the updated proof remains the same ${\Lambda }_i$。

上述算法存在的一个问题是：public parameters $pp$ is $\Theta (q^2)$，可通过如下签名方式改进：

2.2 基于RSA的Vector Commitment实现

RSA assumption定义可参见博客密码学中的各种假设——DL/SDH…。

1）VC.KeyGen($1^k,q$)：随机选择两个$k/2$-bit 的素数$p_1,p_2$，设置$N=p_1{p}_2$，选择$q$个不能整除$\varphi (N)$的$(l+1)$-bit 素数$e_1,\cdots ,e_q$。从$i=1$到$q$，设置$S_i=a^{{\prod }_{j=1,j\ne i}^q{e}_j}$。
Set $pp=(N,a,S_1,\cdots ,S_q,e_1,\cdots ,e_q)$. The message space is $M=\{0,1{\}}^l$。【CRS的length为$\Theta (2q)$，且$p_1,p_2$不在CRS中（需满足RSA assumption，$p_1,p_2$对Prover不可知）。】

2）VC.Com_{pp}($m_1,\cdots ,m_q$)：Compute $C=S_1^{m_1}{S}_2^{m_2}\cdots S_q^{m_q}={\prod }_{i=1}^q{S}_i^{m_i}$ and output $C$ and the auxiliary information $aux=(m_1,\cdots ,m_q)$。

3）VC.Open_{pp}($m_i,i,aux$)：Compute ${\Lambda }_i=\sqrt[e_i]{{\prod }_{j=1,j\ne i}^q{S}_j^{m_j}}\mathrm{m}\mathrm{o}\mathrm{d}N$。【由于$pp$中包含了$a,e_1.\cdots ,e_q$信息，Prover做相应的开$e_i$次方很容易计算。】

4）VC.Ver_{pp}($C,m_i,i,{\Lambda }_i$)：If $m\in M$且$C=S_i^m{\Lambda }_i^{e_i}\mathrm{m}\mathrm{o}\mathrm{d}N$ then output $1$. Otherwise output $0$。

5）VC.Update_{pp}($C,m,m^{‘},i$)：Compute the updated commitment $C^{‘}=C\cdot S_i^{m^{‘}-m}$. Finally output $C^{‘}$ and $U=(m,m^{‘},i)$。

6）VC.ProofUpdate_{pp}($C,{\Lambda }_j,m^{‘},U$)：A client who owns a proof ${\Lambda }_j$, that is valid w.r.t. to $C$ for some message at position $j$, can use the update information $U=(m,m^{‘},i)$ to compute the updated commitment $C^{‘}$ and produce a new proof ${\Lambda }_j^{‘}$ which will be valid w.r.t. $C^{‘}$. We distinguish two cases：

• $i\ne j$：Compute the updated commitment $C^{‘}=C\cdot S_i^{m^{‘}-m}$ while the updated proof is ${\Lambda }_j^{‘}={\Lambda }_j\cdot \sqrt[e_j]{S_i^{m^{‘}-m}}$。【由于$pp$中包含了$a,e_1.\cdots ,e_q$信息，Prover做相应的开$e_j$次方很容易计算。】
• $i=j$：Compute the updated commitment as $C^{‘}=C\cdot S_i^{m^{‘}-m}$ while the updated proof remains the same ${\Lambda }_i$。

同时，Verifier应执行一次验证，确保$pp$中的$S_i$与其中的$a,e_1,\cdots ,e_q$确实满足$S_i=a^{{\prod }_{j=1,j\ne i}^q{e}_j}$。

---

在2018年论文《Batching Techniques for Accumulators with Applications to IOPs and Stateless Blockchains》基于strong RSA assumption in groups of unknown order实现了Vector Commitment，相较于上述实现，做了如下改进：

• 限定了用于commit的vector $m_1,\cdots ,m_q$中各元素为co-prime的，减少了public info $pp$ 中的$(S_1,\cdots ,S_q)$ 参数，减少了CRS的长度；
• 利用Bezout和ShamirTrick算法，实现了batching of non-membership proofs；
• 利用RootFactor算法，在没有$e_1.\cdots ,e_q$的情况下，将计算$e_j$-th root的算法复杂度由$\Theta (q^2)$降为了$\Theta (q\log (q))$，同时再次减少了CRS的长度。

基于以上策略所实现的Vector Commitment，其subvector openings为constant size，public parameters也为constant size（与vector的长度无关）。

详细的算法解析参见博客：
https://blog.csdn.net/mutourend/article/details/102936314
具体的代码实现解析参见博客：
Vector Commitments代码实现 中的2.1和2.2节内容。

---

3. Vector Commitment的应用场景

3.1 Verifiable Databases with Efficient Updates

Verifiable Databases with Efficient Updates（VDB），由Benabbas, Gennaro and Vahlis 在 2011年论文《Verifiable delegation of computation over large datasets》中提出，可用于解决verifiable outsourcing of storage（存储外包）。client资源有限，需要将 a large database 外包给server来存储，client可获取database record，也可更新record。要求：

• For efficiency，client获取record和更新record所需的计算资源应与database的size无关（初始化阶段除外）；
• For security，在client不知情的情况下，server无法篡改database的任何record。

若client不做update操作，针对此static case，可通过message authentication或signature scheme来实现，即client先对database record 签名，然后才将前面后的record发送给server，server ouput的record必须有相应的valid signature。 但是，当client需要做update操作时，该方式不可行——需要有机制来允许client撤销前面的签名。解决方案有：

• accumulators；
• authenticated data structures；
• verifiable computation 可信计算；
• authenticated remote file systems。

Benabbas 等人2011年论文《Verifiable delegation of computation over large datasets》中的方案，relies on a constant size assumption in bilinear groups of composite order, but does not support public verifiability (i.e., only the client owner of the database can verify the correctness of the proofs provided by the server)。

而采用本文的Vector Commitments方案，支持VDB的public verifiability。同时若采用VC based on CDH 方案，则可实现基于standard constant-size assumption的VDB，其efficiency improves over the scheme of Benabbas 的方案 as we can use bilinear groups of prime order。

将database $D$ 表述为由一系列tuples $(x,v_x)$组成，其中$x$为key，$v_x$为相应的value，表示为$D(x)=v_x$。假设key的取值范围为$\{1,\cdots ,q\}$，其中$q=poly(k)$，而DB value为任意的string $v\in \{0,1{\}}^{\ast }$。

基本的流程为：
1）VDB.Setup($1^k,D$)：On input the security parameter $k$ and a database $D$, the setup algorithm is run by the client to generate a secret key $SK$ that is kept private by the client, a database encoding $S$ that is given to the server, and a public key $PK$ that is distributed to all users (including the client itself) who wish to verify the proofs.
2）VDB.Query($PK,S,x$)：On input a database key $x$, the query processing algorithm is run by the server, and returns a pair $\tau =(v,\pi )$.
3）VDB.Verify($PK,x,\tau$)：The public verification algorithm outputs a value $v$ if $\tau$ verifies correctly w.r.t. $x$ (i.e., $D(x)=v$), and an error $\perp$ otherwise.
4）VDB.ClientUpdate($SK,x,v^{‘}$)：The client update algorithm is used by the client to change the value of the database record with key $x$, and it outputs a value $t_x^{‘}$ and an updated public key $P{K}^{‘}$.
5）VDB.ServerUpdate($PK,S,x,t_x^{‘}$)：The server update algorithm is run by the server to update the database according to the value $t_x^{‘}$ produced by the client.

需满足要求：

• security。
• the size of the information stored by the client as well as the time needed to compute verifications and updates must be independent of the size $|D|$ of the database。

若采用Vector Commitment来实现上述Verifiable Databases with Efficient Updates流程：

3.2 Updatable Zero-Knowledge Elementary Databases

Zero knowledge set(ZKS) means that users commit to a set and subsequently prove the (non-)membership of some elements without revealing any further information (not even the cardinality of the committed set).【参见博客 Vector Commitment, Zero-knowledge Set, Zero-knowledge Accumulator等区别】

一般地，ZKS都是基于 trapdoor mercurial commitments
and collision resistant hash functions 来构建的，生成membership proof和non-membership proof。

详细描述见Catalano等人2011年论文《Zero-Knowledge Sets with short proofs》。

等价为：build $q$-mercurial commitments (qTMC) using vector commitments。

使用(concise) vector commitment和standard trapdoor commitment来构建(concise) trapdoor qTMC的流程为：


若想qTMC支持updatable，需要额外增加两个算法：

基于Vector Commitment的详细实现为：