使用卷积神经网络学习描述子(learning-based descriptors)
特征点的检测与匹配是CV领域一个热门的研究方向,首先是对图像进行特征检测,然后为每个特征点分配一个描述子。
后期匹配过程即计算描述子之间的距离,距离越近认为匹配上的概率越大。所以得到精确的描述子是十分重要的。
本文主要回顾了经典的handcrafted描述子,包括SIFT、BRIEF等,以及近年来的前沿研究—通过CNN学习到的描述子,对一些经典论文作了综述。
1. 手工设计的(handcrafted)描述子
描述子(descriptors)主要可以分为浮点型(float descriptors)和二进制(binary descriptors)两类,前者的优点是更精确,后者的优点是速度更快。最具代表性的浮点型描述子毫无疑问是1999年Lowe[1]提出的SIFT(Scale-invariant feature transform)描述子,SIFT描述子性能优异,通过主方向的确定使其具备了旋转不变性,通过高斯差分金字塔(Difference of Gaussian, DoG)的建立使其获得尺度不变性。由于其优异的性能,SIFT描述子在图像检索、增强现实(Augmented Reality, AR)、SLAM等领域应用广泛。
SIFT算法的一大缺点就是慢,当然并不是慢在描述子生成上,而是特征点的检测,但是匹配过程中浮点型描述子需要计算欧氏距离,也大大降低了速度,而且不仅计算慢,对比二进制数,浮点数的存储也需要更大的空间。由于计算机处理二进制数天生的强大能力,大牛们想到用二进制描述子代替浮点型,于是,BRIEF描述子[2]横空出世了。BRIEF描述子的详细算法流程可以看论文原文或者这篇博客 BRIEF特征点描述算法详解。
Notice1: 不同于SIFT算法可以同时检测特征点并生成描述子,BRIEF算法只能生成描述子而无法检测特征点,一般配合ORB[3]等算法一起使用。在特征匹配的时候,BRIEF描述子只需要计算汉明距离(Hamming Distance),极大地提升了运算速度。
Notice2: SIFT描述子与BRIEF描述子都是128维,维度太高会导致维度灾难(Curse of Dimensionality),维度太低会导致描述子信息量不足,举个例子,

假设只使用维度为8的描述子,那么对于二进制描述子而言,最多只能描述 2 8 = 256 2^8 = 256 28=256个特征点,对于某些特征点数超过256的图片而言,不同特征点势必有重复的描述子,这是远远不够的。
2. 基于学习(learning based )的描述子
handcrafted描述子的生成主要是通过特征点周围像素点的像素值确定,也就是说描述子由特征点的邻域确定,那于是大牛们开始思考,我们能不能收集一块以特征点为中心的小patch,然后通过机器学习的方法学到描述子呢?说到这就绕不开一个重要的数据集—UBC Phototour[4],UBC Phototour也称Brown数据集,该数据集之所以叫Phototour,是因为图像patch分别截取自罗马、巴黎和优胜美地的图片,所以该数据集分为三个子数据集,一般是训练其中一个测试另外两个。数据集的每个patch都是 64 × 64 64\times64 64×64的灰度图,而且在官方文档中给出了匹配信息。该数据集的衡量指标比较单一,采用了FPR95作为唯一的指标,具体可见博文Brown 数据集和评价指标。
有了数据集和评价指标之后,就是设计算法对数据集进行训练和测试了。描述子的学习实质上是一种image embedding的学习,也就是通过学习图像patch得到一个向量,这个向量在欧式空间的分布与原patch相同,即如果patch相似或匹配上,则向量的欧氏距离更近,没匹配上的两个patch的向量距离更远。如果把匹配上的patch当做类内(intra-class),不匹配的patch当做类间(inter-class),那么学习描述子问题与线性判别分析(linear discriminant analysis, LDA)的思想相同,都是最小化类内间距,最大化类间间距,所以个人理解描述子的学习更多属于度量学习的范畴。另外,image embedding是一个很大的研究方向,包括人脸识别、行人重识别(Re-ID)、细粒度图像分类(Fine-grained Category Detection)、图像检索(Image Retrieval)等很多领域都使用了image embedding的思想。很容易理解的,拿Re-ID举例,同一个人的图像,生成的embedding向量应该尽可能接近,不同的人的向量在欧式空间需要尽可能远离,才能把同一个人重新识别出来。另外提一嘴,人脸识别三五年前是很热门的研究方向,但是现在已经落地,所以研究的人少了起来,但是Re-ID和细粒度图像分类都是这两年非常热门的研究方向。
2015年ICCV的论文DeepDesc(Discriminative Learning of Deep Convolutional Feature Point Descriptors) [5]开启了使用神经网络训练学习描述子的先河。同年的CVPR还有一篇论文Learning to Compare Image Patches via Convolutional Neural Networks [6]也是做的CNN学习描述子的,而且引用也很高,但是DeepDesc对后期的研究影响更大一点。DeepDesc使用了下图所示的三层Siamese网络作为基础来学习描述子,两个patch通过共享圈子的CNN分支得到描述子D,然后计算 D ( x 1 ) D(x_1) D(x1)和 D ( x 2 ) D(x_2) D(x2)的距离并通过损失函数优化CNN参数。
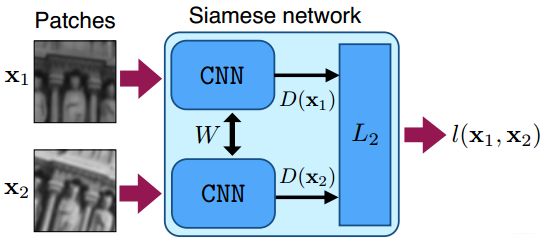
DeepDesc使用 L 2 L_2 L2范数作为描述子在欧式空间距离的度量,损失函数如下: l ( x 1 , x 2 ) = { ∣ ∣ D ( x 1 ) − D ( x 2 ) ∣ ∣ 2 , p 1 = p 2 m a x ( 0 , C − ∣ ∣ D ( x 1 ) − D ( x 2 ) ∣ ∣ 2 ) , p 1 ≠ p 2 l(x_1, x_2)=\left\{ \begin{array}{rcl} &||D(x_1)-D(x_2)||_2, &p_1=p_2\\ &max(0, C-||D(x_1)-D(x_2)||_2), &p_1\not=p_2\\ \end{array} \right. l(x1,x2)={∣∣D(x1)−D(x2)∣∣2,max(0,C−∣∣D(x1)−D(x2)∣∣2),p1=p2p1=p2在上式中,损失函数分为两种情况, p 1 = p 2 p_1=p_2 p1=p2指的是输入Siamese网络的两个patch是匹配上的,此时,它们的描述子应该尽可能近,所以此时应该最小化 ∣ ∣ D ( x 1 ) − D ( x 2 ) ∣ ∣ 2 ||D(x_1)-D(x_2)||_2 ∣∣D(x1)−D(x2)∣∣2; p 1 ≠ p 2 p_1\not=p_2 p1=p2时应该最大化 ∣ ∣ D ( x 1 ) − D ( x 2 ) ∣ ∣ 2 ||D(x_1)-D(x_2)||_2 ∣∣D(x1)−D(x2)∣∣2。这种损失函数一般被称为Siamese loss或者pairwise loss。
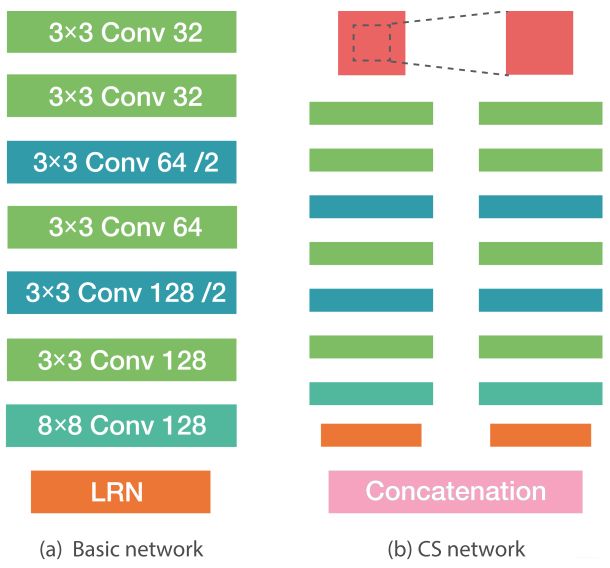
2017年,发表在CVPR的论文L2-Net[7]提出了使用更深的神经网络来学习描述子,其网络结构如下图所示,不同于DeepDesc只使用三层CNN进行训练和学习,L2-Net共包含七层卷积层和最后一层LRN(Local Response Normalization layer)层,其中,网络的输出是 32 × 32 32\times32 32×32大小的patch,将原图resize为1/2,在每一层卷积层后面都跟了BN层,最后的LRN层是用来将128维的描述子进行标准化,使其成为长度为1单位向量。L2-Net也提出了一些新的损失函数,详细可见原文,但是贡献最大的还是他的网络结构,因为后期大部分工作都采用了该八层网络结构来学习描述子。
发表在2017年NIPS上的HardNet[8]同样是很有影响力的工作,近年顶会上很多工作都是基于HardNet改进。HardNet使用的网络结构与L2-Net完全相同,损失函数采用了triplet loss。triplet loss最早在人脸识别领域被Facenet提出[9],也是用来学习人脸图片的embedding,公式为 L = m a x ( d ( a , p ) − d ( a , n ) + m a r g i n , 0 ) L=max(d(a,p)−d(a,n)+margin,0) L=max(d(a,p)−d(a,n)+margin,0),上式中, a a a指的是anchor, p p p指的是positive, n n n指的是negtive。anchor和positive指的是同一个人的人脸,anchor和negtive是不同的人脸,该损失函数最小化类内 a a a与 p p p距离,最大化类间 a a a与 n n n距离,且鼓励 d ( a , n ) d(a,n) d(a,n)与 d ( a , p ) d(a,p) d(a,p)的差值为margin,详情可见博客Triplet-Loss原理及其实现、应用。
HardNet的一个motivation就是在描述子学习中,匹配上的patch可以看做是 a a a与 p p p,未匹配上的patch可看做是 a a a与 n n n,同时HardNet对triplet loss做出了改进,挖掘了最难的负样例,损失函数如下: L = 1 n ∑ i = 1 n m a x ( 0 , 1 + d ( a i , p i ) − m i n ( d ( a i , p j m i n ) , d ( a k m i n , p i ) ) ) L= \frac{1}{n}\sum_{i=1}^n max(0,1+d(a_i,p_i)-min(d(a_i,p_{j_{min}}),d(a_{k_{min}},p_i))) L=n1i=1∑nmax(0,1+d(ai,pi)−min(d(ai,pjmin),d(akmin,pi)))其中 d ( a i , p i ) d(a_i,p_i) d(ai,pi)指的是匹配上的patch得到的描述子的距离, a a a与 p p p下标相等则说明它们是匹配上的,不同则说明不匹配。HardNet通过 m i n ( d ( a i , p j m i n ) , d ( a k m i n , p i ) ) min(d(a_i,p_{j_{min}}),d(a_{k_{min}},p_i)) min(d(ai,pjmin),d(akmin,pi))挖掘了距离最近的未匹配的描述子向量。
光看公式可能有点抽象,下面说一说具体的实现。首先loss是作用在一个batch上,论文讨论了batch size对最后实验结果的影响,batch size小于1024时,batch size越大实验结果越好(这个很容易理解,batch size越大,就能挖掘到越难的负样例),但是1024和2048的batch size实验结果相差无几,所以论文中选择了1024作为最后的batch size。论文维持了一个距离矩阵 D = { d i j } ∈ R 1024 × 1024 D=\{d_{ij}\}\in R^{1024\times1024} D={dij}∈R1024×1024,其中 d i j d_{ij} dij指的是描述子 a i a_{i} ai与 p j p_{j} pj的距离,且当 i = j i=j i=j时 a i a_{i} ai与 p j p_{j} pj为匹配上的描述子,所以优化目标是最小化 D D D的对角线元素,最大化 D D D的非对角线元素。注意距离矩阵 D D D并不是对称阵,因为 d ( a i , p j ) d(a_i,p_j) d(ai,pj)与 d ( a j , p i ) d(a_j,p_i) d(aj,pi)并不相等。论文首先取出了 D D D的对角线元素 d ( a i , p i ) ∈ R 1024 d(a_i,p_i)\in R^{1024} d(ai,pi)∈R1024,然后对每一行取最小值得到 d ( a i , p j m i n ) ∈ R 1024 d(a_i,p_{j_{min}})\in R^{1024} d(ai,pjmin)∈R1024,再对每一列取最小值 d ( a k m i n , p i ) ) ∈ R 1024 d(a_{k_{min}},p_i))\in R^{1024} d(akmin,pi))∈R1024,最后比较 d ( a i , p j m i n ) d(a_i,p_{j_{min}}) d(ai,pjmin)与 d ( a k m i n , p i ) d(a_{k_{min}},p_i) d(akmin,pi)得到 m i n ( d ( a i , p j m i n ) , d ( a k m i n , p i ) ) min(d(a_i,p_{j_{min}}),d(a_{k_{min}},p_i)) min(d(ai,pjmin),d(akmin,pi))作为最难的负样例。
3. 总结与展望
通过上述论文可以看出,描述子的学习可以归为image embedding这个大的研究方向,主要是使用度量学习的理论获得一个具有区分性的描述向量,核心就是一句话:最小化匹配描述子的欧氏距离,最大化未匹配描述子的欧氏距离。近年来每个顶会都有三四篇关于描述子学习的论文,说明这还算是一个处于上升期的方向,而且以后就算这玩意不火了,没人愿意研究了(主要是真的没卵用),还可以转去做Re-ID或者图像检索嘛哈哈。
[1]Lowe D G. Object recognition from local scale-invariant features[C]. ICCV 1999.
[2] Calonder M, et al. Brief: Binary robust independent elementary features[C]. ECCV 2010.
[3] Rublee E, et al. ORB: An efficient alternative to SIFT or SURF[C]. ICCV 2011.
[4] Winder S A J, Brown M. Learning local image descriptors[C]. CVPR 2007.
[5] Simo-Serra E, et al. Discriminative learning of deep convolutional feature point descriptors[C]. ICCV 2015.
[6] Zagoruyko S, Komodakis N. Learning to compare image patches via convolutional neural networks[C]. CVPR 2015.
[7] Tian Y, Fan B, Wu F. L2-net: Deep learning of discriminative patch descriptor in euclidean space[C]. CVPR 2017.
[8] Mishchuk A, et al. Working hard to know your neighbor’s margins: Local descriptor learning loss[C]. NIPS 2017.
[9] Schroff F, et al. Facenet: A unified embedding for face recognition and clustering[C]. CVPR 2015.