Keyboard Free (计算几何)2020牛客多校第二场
题目描述
Given three concentric circles whose radiuses are r_1, r_2, r_3r1,r2,r3 respectively, and {A,B,C}A,B,C are the moving points on the given three circles respectively. Determine the expected area of \triangle ABC△ABC.
输入描述:
The first line contains one integer T~(1 \leq T \leq 1000)T (1≤T≤1000), denoting the number of test cases. For each test case: One line containing three integers r_1, r_2, r_3~(1\leq r_1,r_2,r_3 \leq 100)r1,r2,r3 (1≤r1,r2,r3≤100), denoting the radiuses of three given concentric circles.
输出描述:
Print {T}T lines each containing one real number with one decimal places after the decimal point, denoting the answer to curresponding test case.
It's guaranteed that the second decimal place after the decimal point is neither 4 nor 5.
示例1
输入
2 1 1 1 2 3 5
输出
0.5 5.5
说明
For test case 1, the accurate answer is \frac{3}{2\pi} = 0.47746482927568600730665129011754\cdots2π3=0.47746482927568600730665129011754⋯.
首先感谢“世界第一中单”cyt上午的教学!
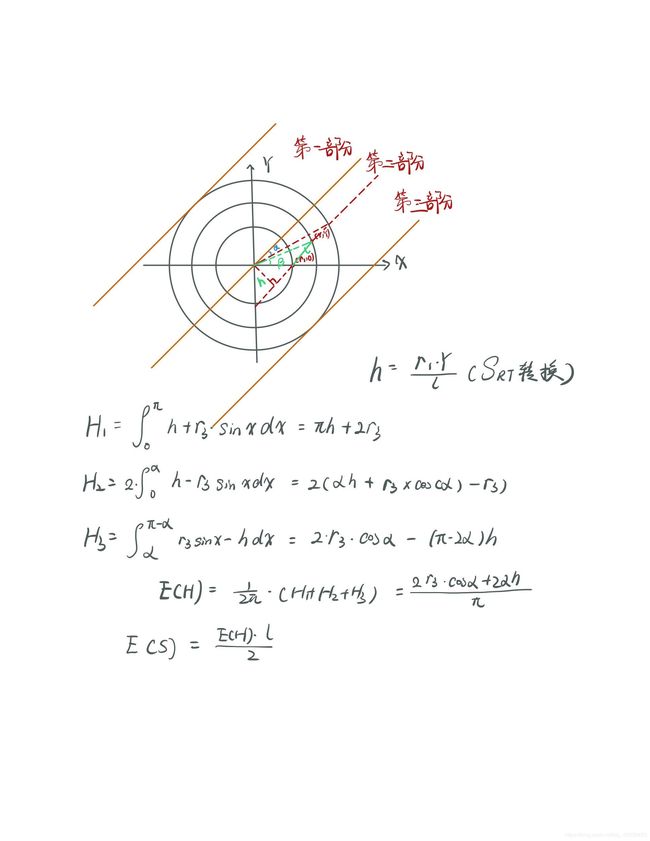
思路:先对输入的r1,r2,r3进行排序,r1 <=r2 <=r3
因为可以对3个圆进行旋转,默认r1上的点不变为(r1,0),将r2圆分为1000份并遍历上面的点(x,y)
之后如下:
代码:
#include
using namespace std;
const double pi = acos(-1.0);
double r1, r2, r3;
int main() {
int t;
cin>>t;
while(t--)
{
cin>>r1>>r2>>r3;
if (r1 > r2) swap(r1, r2);
if (r2 > r3) swap(r2, r3);
if (r1 > r2) swap(r1, r2);
double e = 2.0 * pi / 1000;
double ans = 0;
for (int i = 1; i <= 1000; i++) {
double b = i * e, x = r2 * cos(b), y = r2 * sin(b);
double l = sqrt((x - r1) * (x - r1) + y * y);
double h=r1*y/l;
double a=asin(h/r3);
double Eh=(2*r3*cos(a)+2*a*h)/pi;
ans += 0.5 * l * Eh;
}
printf("%.1f\n", ans / 1000);
}
return 0;
}
(代码挺短不是吗)