最长上升子序列(LIS)解析,子集树求解
文章目录
- LIS的定义
- 子集树解法
- LIS子集树求解
LIS的定义
最长上升子序列(Longest Increasing Subsequence) , 简称LIS , 也有些情况求的是最长非降序子序列 , 二者区别就是序列中是否可以有相等的数 . 假设我们有一个序列 b i , 当b1 < b2 < … < bS的时候 , 我们称这个序列是上升的 . 对于给定的一个序列(a1, a2, …, aN) , 我们也可以从中得到一些上升的子序列(ai1, ai2, …, aiK) , 这里1 <= i1 < i2 < … < iK <= N , 但必须按照从前到后的顺序 .
比如 , 对于序列(1, 7, 3, 5, 9, 4, 8) , 我们就会得到一些上升的子序列 , 如(1, 7, 9), (3, 4, 8), (1, 3, 5, 8)等等 , 而这些子序列中最长的(如子序列(1, 3, 5, 8) , 它的长度为4 , 因此该序列的最长上升子序列长度为4 .
子集树解法
对于LIS问题的解法 , 网上出现最多的就是 , 动态规划 , 贪心+二分 . 那问题来了 , 要是这两种用的不熟练解不了题怎么办 , 宣告GG ? 那是不可能的 , 接下来就来看看相对简单的子集树解题.
什么叫子集树?
就是以首元素作为根节点 , 它的孩子结点是下一个元素 . 通过对左枝干置为1 , 右枝干置为0 , ( 遇到1打印数字 , 遇到0不打印数字 ) , 就可以产生全排列组合 .
形如: (A,B,C,D)

例如: int arr[] = {1,2,3};
用过子集树得到如下输出
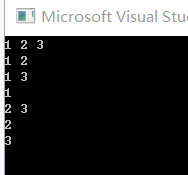
那么 , 如何实现子集树呢 , 就一句话递归调用两次自身函数就是二叉树 . (调用三次就是三叉树)
框架代码如下:
/*
函数中 , 调用两次func1()就相当于创建了一个二叉树
这是一个全排列算法
通过对左枝干置为1
右枝干置为0
遇到1打印数字 , 遇到0不打印数字
最后的结果就是这3个数的全排列组合
三层在第四层操作 , 能够打印全
*/
void func1(int ar[], int i, int len, int br[])
{
if (i == len)
{
//访问子集 , 并打印
for (int j = 0; j < len; ++j)
{
if (br[j] == 1)
cout << ar[j] << " ";
}
cout << endl;
}
else
{
/*
两个递归调用就是二叉树
三个递归调用就是三叉树
四个递归调用就是四叉树
*/
br[i] = 1; //将左树枝置为1
func(ar, i + 1, len, br); //访问i节点的左孩子
br[i] = 0; //将右树枝置为0
func(ar, i + 1, len, br);//访问i节点的右孩子
}
}
#endif
int main()
{
int ar[] = { 1,2,3 };
int br[3] = { 0 };
func1(ar, 0, 3, br);
return 0;
}
看完上述代码, 你可能还有些疑惑 , 3是怎么输出的 . 实际上 , 我们将枝干置为 0 或 1 . 1 输出 , 0 不输出 . 而3却没有显示枝干 , 那么我们不妨将之前的图稍作修改 , 以便更好的理解代码
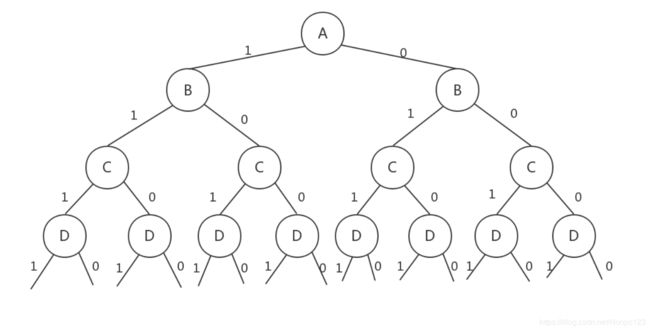
这样是不是就一幕了然了 .
LIS子集树求解
根据子集树可以求出所有子集 , 那么只要我们去判断每个子集是否为上升子集 , 如果是上升子集就记录长度 . 最后即可得到最长的上升子集的长度
代码如下:
//LIS算法 , 子集树实现
int _fin = -1; //最终输出
int _count = 0; //记录子集长度
void func1(int* arr, int i, int len, int* brr)
{
_count = 0;
int _max = -1;
//求最长升序子集(LIS)
for (int j = 0; j < len; ++j)
{
if (brr[j] == 1)
{
if (arr[j] > _max)
{
_max = arr[j];
++_count;
}
else
{
break;
_count = 0;
}
}
}
_fin = max(_fin,_count);
}
else
{
brr[i] = 1;
func1(arr, i + 1,len,brr);
brr[i] = 0;
func1(arr, i + 1, len, brr);
}
}
int main()
{
//int ar[] = { 1, 7, 3, 5, 9, 4, 8 };
int ar[] = { 2,7,1,5,6,4,3,8,9 };//2 7 1 5 6 4 3 8 9
int br[9] = { 0 };
func1(ar, 0, 9, br);
cout << _fin << endl;
return 0;
}
