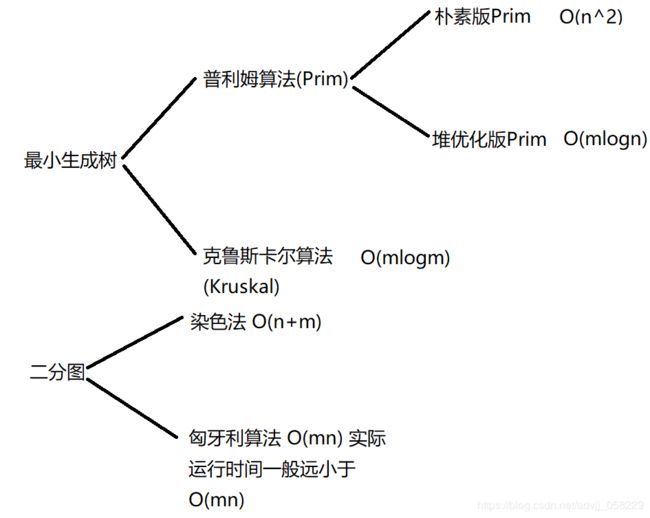
最小生成树

相关概念：

连通图：在无向图中，若任意两个顶点$v_i$与$v_j$都有路径相通，则称该无向图为连通图。
强连通图：在有向图中，若任意两个顶点$v_i$与$v_j$都有路径相通，则称该有向图为强连通图。
连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接两个顶点的代价，称这种连通图叫做连通网。
生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。
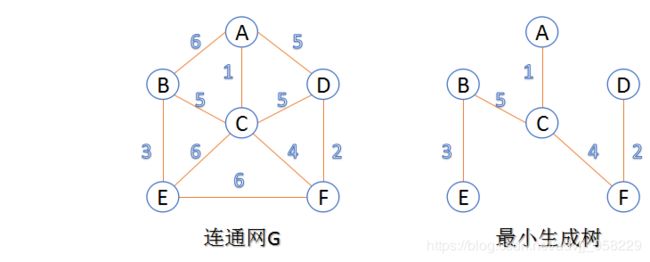
最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

1. 普利姆算法（Prim）

- 朴素版Prim$O(n^2)$

算法原理

s表示当前已经在连通块中的所有点 
 1. dist[i] <--- +INF
 2. for(int i = 0;i < n;i++)
	t<---找到集合外距离最近的点
	用t更新其他点到集合的距离。
	st[t] = true

#include 
#include 
#include 

using namespace std;

const int N = 510,INF = 0x3f3f3f3f;

int n,m;
int g[N][N];
int dist[N];
bool st[N];

int prim(){
    memset(dist,0x3f, sizeof dist);
    
    int res = 0;
    for(int i = 0;i < n;i++){
        int t = -1;
        for(int j = 1;j <= n;j++){
            if(!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        }
        if(i && dist[t] == INF)
            return INF;
        if(i)
            res += dist[t];
        st[t] = true;
        for(int j = 1;j <= n;j++)
            dist[j] = min(dist[j],g[t][j]);
    }
    return res;
}

int main(){
    
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(false);
    
    cin >> n >> m;
    
    memset(g,0x3f, sizeof g);
    
    while(m--){
        int a,b,c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = min(g[a][b],c);
    }
    
    int t = prim();
    if(t == INF)
        puts("impossible");
    else
        cout << t << endl;
    
    return 0;
}

- 堆优化版Prim$O(mlo{g}_n)$

2.克鲁斯卡尔算法（Kruskal）$O(mlo{g}_m)$

算法原理

1.将所有边按权重从小到大排序 O(mlogm)
2.枚举每条边a,b,权重c  O(m)
	if a,b不连通
	将这条边加入集合中

#include
#include
#include

using namespace std;

const int N = 100010;

int n, m;
int p[N];

struct Edge{

	int a, b, w;
	bool operator< (const Edge &W)const {
		return w < W.w;
	}

}edges[N];

int find(int x) {
	if (p[x] != x)
		p[x] = find(p[x]);
	return p[x];
}

int main() {

	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		int a, b, w;
		cin >> a >> b >> w;
		edges[i] = { a,b,w };
	}

	sort(edges, edges + m);

	for (int i = 1; i <= n; i++)
		p[i] = i;
	int res = 0, cnt = 0;
	for (int i = 0; i < m; i++) {
		int a = edges[i].a, b = edges[i].b, w = edges[i].w;
		a = find(a), b = find(b);
		if (a != b) {
			p[a] = b;
			res += w;
			cnt++;
		}
	}

	if (cnt < n - 1)
		puts("impossible");
	else
		cout << res << endl;

	return 0;
}

3.二分图

当且仅当图中不含奇数环
奇数环：环当中边的数量是奇数。

- 染色法$O(n+m)$

//染色法
for(int i = 1;i <= n;i++)
	if i未染色
		dfs(i,1)

acwing860.染色法判定二分图
实例

#include
#include
#include

using namespace std;

const int N = 100010, M = 200010;

int n, m;
int h[N], e[M], ne[M], idx;
int color[N];
bool st[N];

void add(int a,int b) {
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}

bool dfs(int u, int c) {
	color[u] = c;
	for (int i = h[u]; i != -1; i = ne[i]) {
		int j = e[i];
		if (!color[j]) {
			if (!dfs(j, 3 - c))
				return false;
		}
		else if(color[j] == c){
			return false;
		}
	}
	return true;
}

int main() {

	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(false);

	cin >> n >> m;

	memset(h, -1, sizeof h);

	while (m--) {
		int a, b;
		cin >> a >> b;
		add(a, b), add(b, a);
	}

	bool flag = true;
	for (int i = 1; i <= n; i++) {
		if (!color[i]) {
			if (!dfs(i, 1)) {
				flag = false;
				break;
			}
		}
	}

	if (flag)
		puts("Yes");
	else
		puts("No");

	return 0;
}

- 匈牙利算法$O(mn)$，实际运行时间一般远小于$O(mn)$

acwing861.二分图的最大匹配
实例

#include 
#include 
#include 

using namespace std;

const int N = 510, M = 100010;

int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool find(int x)
{
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true;
            if (match[j] == 0 || find(match[j]))
            {
                match[j] = x;
                return true;
            }
        }
    }

    return false;
}

int main()
{
    scanf("%d%d%d", &n1, &n2, &m);

    memset(h, -1, sizeof h);

    while (m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }

    int res = 0;
    for (int i = 1; i <= n1; i ++ )
    {
        memset(st, false, sizeof st);
        if (find(i)) res ++ ;
    }

    printf("%d\n", res);

    return 0;
}