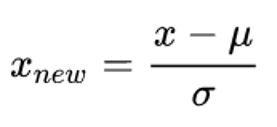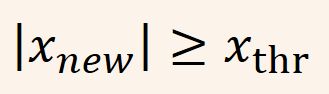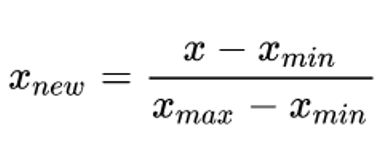数据清洗
目录
特征编码
序号编码
独热编码
二进制编码
离散化
缺失值填补
异常值处理
IQR
Z-score
DBSCAN
孤立森林
归一化
标准化
补充
参考博客
这里我们不说图片数据,图片数据的处理有专门的CV方向,我们就来说说文本数据或者“数字数据”。
对于文本数据,显然计算机没办法处理,比如说“星期一”,计算机看不懂,怎么办?答:可以变成数字。
注:其实有些算法是可以处理文本数据的,不需要进行一些特征编码操作。另外对于数据类型的划分,我们一般会划分为结构化数据和非结构化数据,文本和图像都属于非结构化数据。
对于数字数据,我们可以分为离散型数据(类别型特征)与连续型数据,就是字面意思。
补充说明一点,监督学习一般使用两种类型的目标变量,也就是待预测的值:标称型和数值型。
标称型 标称型目标变量的结果只在有限目标集中取值,如真与假(标称型目标变量主要用于分类)
数值型 数值型目标变量则可以从无限的数值集合中取值,如0.100,42.001等 (数值型目标变量主要用于回归分析)
你会发现也就是换了个说法而已,万变不离其宗。
问题来了,我们拿到数据之后要对数据做什么最初的处理呢?
特征编码
从数据描述中可以看到数据的格式等信息,通常我们都会对特征进行一定的再编码操作,说很很专业,其实所谓的特征编码,也就是类似于”转换数据类型“。
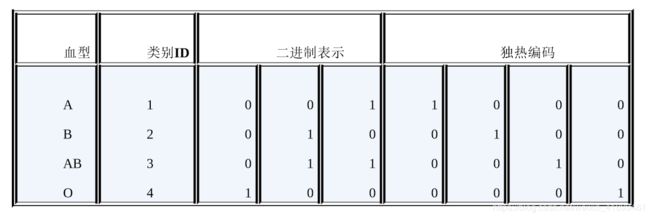
类别型特征(Categorical Feature)主要是指性别(男、女)、血型(A、B、 AB、O)等只在有限选项内取值的特征。对于逻辑回归、支持向量机等模型来说,类别型特征必须经过处理转换成数值型特征才能正确工作。
这里涉及到的”数据类型转换“,方法通常有序号编码(Ordinal Encoding)、独热编码(One-hot Encoding)、二进制编码 (Binary Encoding),都很简单。
我们首先来一个经验性的总结:对于类别型数据,我们可以简单的分为”有序“的数据和”无序“的数据,比如说(男、女)显然是无序的,但是(低、中、高)显然就是有序的,对于这两类数据,我们的处理方法可不太一样。
序号编码
序号编码通常用于处理类别间具有大小关系的数据。例如成绩,可以分为低、中、高三档,并且存在“高>中>低”的排序关系。序号编码会按照大小关系对类别型特征赋予一个数值ID,例如高表示为3、中表示为2、低表示为1,转换后依然保留了大小关系。
注意喔,数字可不仅仅就是数字那么简单,在很多算法里面,数字之间是有”距离“信息的,比如123和124在某些算法(比如KNN)中就不是同样的编码,因为4比2大2,而3比2大1。
独热编码
通常用于处理类别间不具有大小关系的特征。例如血型,一共有4个取值(A型血、B型血、AB型血、O型血),独热编码会把血型变成一个4维稀疏向量,A型血表示为(1, 0, 0, 0),B型血表示为(0, 1, 0, 0),AB型表示为(0, 0, 1, 0),O型血表示为(0, 0, 0, 1)。
独热编码使用了稀疏向量来节省空间(这里涉及到一个复杂的东西——稀疏向量,现在我们简单的理解为系数矩阵),这显然提高了特征的维度,说的简单点就是本来是一列数据,结果现在变成了4列,但我们可以通过特征选择来降低维度。
请注意,高维度特征会带来几方面的问题。一是在K近邻算法中,高维空间下两点之间的距离很难得到有效的衡量;二是在逻辑回归模型中,参数的数量会随着维度的增高而增加,容易引起过拟合问题;三是通常只有部分维度是对分类、预测有帮助,因此可以考虑配合特征选择来降低维度。
二进制编码
先用序号编码给每个类别赋予一个类别ID,然后将类别ID对应的二进制编码作为结果,本质其实是哈希映射。从下图中可以看出,二进制编码的维数少于独热编码,并且节省了存储空间。
离散化
前面洋洋洒洒讲了半天关于类别型特征的处理,这里简单的提一下对于连续型特征的离散化处理,这在决策树等算法中是有应用的。
很简单,比如说0~100这100个数字,它们是连续的,假设这是得分情况吧!我们现在不需要这么细节的数据了,我们觉得简单一点可能会更好一些,于是我们把0~59分的数据全部改成”D“,60~79分是”C“,80~89分是”B“,90~100分是”A“。你会发现,本来连续的特征,被我们碎片化了,也就是所谓的”离散化“操作。
缺失值填补
数据有缺失,这是超级常见的现象,怎么办呢?有这么几个方法。
- 特征均值填充
- 特殊值填充
- 忽略缺失值样本
- 使用相似样本的均值填充
- 使用机器学习算法预测缺失值
在这里就不详细描述了,通常我们都不建议使用方法123,这回带来较大的误差,毕竟这些方法填补的数据,极有可能都是不符合实际情况的”垃圾数据“。没办法,数据科学家们最为头大的事情之一,就是数据清洗阿!
异常值处理
缺失值一眼就看见了,异常值可不是,所以首先我们需要知道如何识别出异常值,也就是异常值检测。这里的内容大家可以参考https://www.zhihu.com/question/38066650。
IQR
观察箱型图,或者通过IQR(InterQuartile Range)计算可以得到数据分布的第一和第四分位数,异常值是位于四分位数范围之外的数据点。
这个方法真的很简单,因为只需要给数据排个序就行了,显然过于笼统,但在实际场景中,观察箱型图仍然是一个很好的探索数据分布的方法。
毕竟,所有复杂的探索,都是从最开始简单的探索一步步得来的嘛!
Z-score
这个方法也很好理解,将一列特征数据做标准化之后,数据的绝对值大于某一阈值的话,我们就认为它是异常值。
所谓的标准化(Standardization)就是下面这个公式:
里面的符号很眼熟,也就是该列特征的均值和标准差,标准化之后的数据大于某个阈值,那么它就是离群点,一般设置为2.5、3.0和3.5。
Z-score也就是给数据做了一个线性变换,IQR取4分位数,百分之25的位置,那么Z-score完全可以理解为取了百分之5左右的位置,其实大同小异。
DBSCAN
该技术基于DBSCAN聚类方法,DBSCAN是一维或多维特征空间中的非参数,基于密度的离群值检测方法。,这其实是模式识别中聚类的方法之一。
(待补充)
孤立森林
该方法是一维或多维特征空间中大数据集的非参数方法,其中的一个重要概念是孤立数。
(待补充)
这两个算法博主真没用过,所以也要学一下,笔记上也没记...
数据处理完毕之后,对于像KNN这样的算法,我们还不能直接把数据丢进去训练,还需要做一些归一化 / 标准化的操作,这会有很多的好处。
归一化
将数据映射到指定的范围内,用于去除不同维度数据的量纲以及量纲单位。常见的映射范围有 [0, 1] 和 [-1, 1] ,最常见的归一化方法就是 Min-Max 归一化(线性函数归一化)。
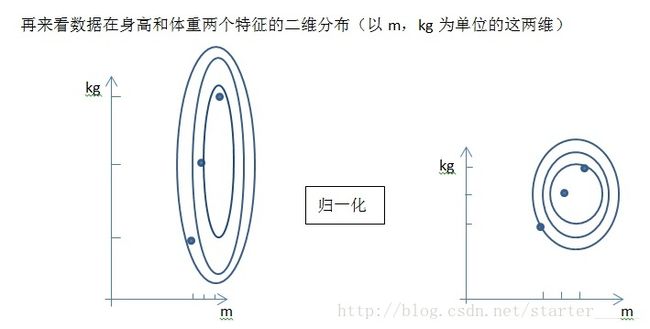
归一化使各个特征维度对目标函数的影响权重是一致的(即使得那些扁平分布的数据伸缩变换成类圆形),可以提高迭代的速率和精度 ;但鲁棒性较差,比较适合传统精确小数据场景。
标准化
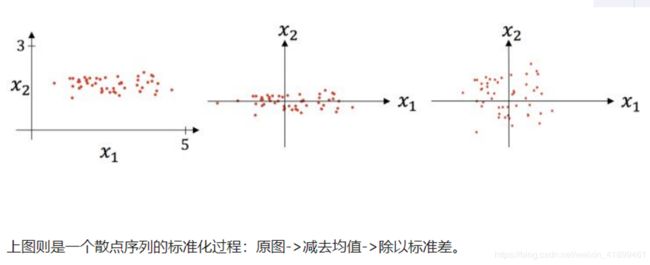
标准化其实前面已经提到了,也就是Z-score标准化。
数据集变成了一个均值为 0 ,方差为 1 的分布。在梯度下降中,可以提高迭代速率,提升效率。
说了半天归一化/标准化,它们是干嘛的呢?
这里先补充一点,大家可以看出,对数据进行一些”变换“,比如说线性变化,当然是为了更好地服务于算法,也会有一些比较不常用的变换,可能效果也不错,比如说log变换,把所有的数据做一个log。
补充
归一化 / 标准化的好处。
(1)提升梯度下降的速率和精度
未归一化 / 标准化之前:
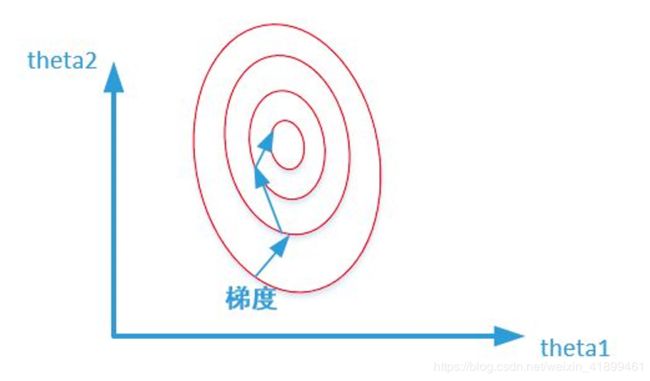
这里稍微解释一下这个图,红色的是等高线,比如说最外面的一圈红线,在这上面的任何一个点所计算出的损失函数的值都是相同的。最里面一圈就是梯度下降算法的近似参数目标。
未归一化 / 标准化之前的梯度下降,梯度的方向为垂直等高线的方向而走之字形路线,这样会使迭代很慢。
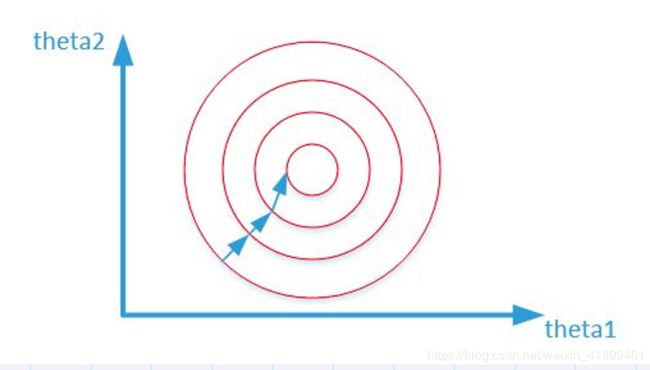
归一化 / 标准化之后:
数据更为规整使得参数的等高线也更加平滑,几乎沿着固定的方向执行参数的更新,可以选取更大的步长,梯度下降的速率也会更加快。
注:不是所有算法都需要用到用到梯度下降,所以也不是所有算法都需要对数据进行归一化 / 标准化处理,比如说决策树以及基于决策树的集成学习等算法就不用作此处理。
(2)提升模型的精度
在一些涉及到距离度量的算法中,比如KNN,纲量不统一带来的问题就是不同的特征对于距离的贡献度会不一样,所以归一化 / 标准化很有必要,它可以让各个特征对结果做出的贡献相同。
举个小例子,分析一个人的身高和体重对健康的影响,如果 使用米(m)和千克(kg)作为单位,那么身高特征会在1.6~1.8m的数值范围内,体重特征会在50~100kg的范围内,分析出来的结果显然会倾向于数值差别比较大的体重特征。想要得到更为准确的结果,就需要进行Normalization处理,使各指标处于同一数值量级,以便进行分析。
(3)深度学习中可以防止模型梯度爆炸。
如何选择归一化还是标准化呢?
归一化和标准化实质都是线性变换,是缩放和平移,不会改变原始数据的数值排序。当数据较为集中时,标准化之后会更加分散,当数据本身分布很广,那么标准化之后数据将会更加集中。通常来说标准化后的数据分布一定比归一化之后的数据分布更广,毕竟归一化是映射到[-1,1]之间嘛。
- 如果对输出结果范围有要求,用归一化;
- 如果数据较为稳定,不存在极端的最大最小值,用归一化;
- 如果数据存在异常值和较多噪音,用标准化,可以间接通过中心化避免异常值和极端值的影响;
- 在分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候,第二种方法(Z-score standardization)表现更好;
- 在不涉及距离度量、协方差计算、数据不符合正态分布的时候,可以使用第一种方法或其他归一化方法。比如图像处理中,将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。如果数据的初始分布接近正态分布,那么显然应该有标准化来处理;
- 归一化适合小数据量,标准化适合大数据量;
- 归一化改变了样本分布,而标准化不改变样本分布(不是很懂)。
参考博客
https://www.zhihu.com/question/38066650
https://blog.csdn.net/starter_____/article/details/79215684
https://blog.csdn.net/zbc1090549839/article/details/44103801