感知器(perceptron)模型分析及实现
感知器模型分析及实现
- 1. 感知器模型
- 2. 几何意义
- 3. 感知器模型的训练
- 4. 批处理训练过程
- 4.1 训练数据的规范化
- 4.2 批处理感知器算法
- 实现代码
\qquad 感知器 ( p e r c e p t r o n ) (perceptron) (perceptron) 本质上是一个线性模型,可以实现“线性分类”。
1. 感知器模型
\qquad 假设输入样本 x = [ x 1 , x 2 , ⋯ , x m ] T ∈ R m \boldsymbol x=[x_1,x_2,\cdots,x_m]^T\in R^m x=[x1,x2,⋯,xm]T∈Rm,感知器实现线性分类的效果主要取决于权值 w = [ w 1 , w 2 , ⋯ , w m ] T \boldsymbol w=[w_1,w_2,\cdots,w_m]^T w=[w1,w2,⋯,wm]T 和偏置 b b b 的大小。
\qquad 感知器包含一个线性组合器 ( l i n e a r c o m b i n e r ) (linear\ combiner) (linear combiner)和激活过程 ( a c t i v a t i o n ) (activation) (activation),其结构如图 1 1 1 所示:
\qquad 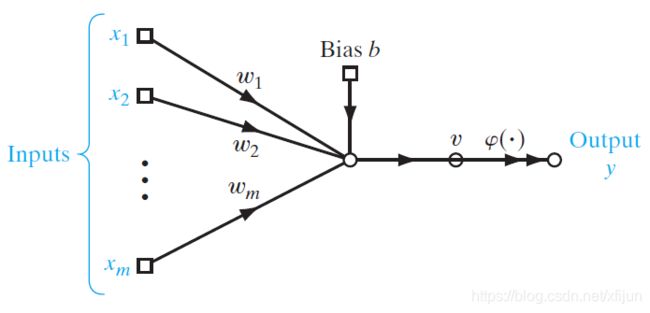
图1From Fig 1.1 《Neural Networks and Learning Machines》
\qquad 显然,由图 1 1 1 可以得到:
( 1 ) \qquad(1) (1) 线性组合器的输出: v = w T x + b v=\boldsymbol w^T\boldsymbol x+b v=wTx+b
( 2 ) \qquad(2) (2) 感知器的输出是对线性组合器的输出进行激活的结果: y = φ ( v ) y=\varphi(v) y=φ(v)
\qquad 常用的激活函数 ( a c t i v a t i o n f u n c t i o n ) (activation\ function) (activation function) 可以是符号函数 s g n ( ⋅ ) sgn(\cdot) sgn(⋅),本文采用的是:
y = φ ( v ) = { 1 , w T x + b > 0 0 , w T x + b ≤ 0 \qquad\qquad y=\varphi(v)=\left\{\begin{matrix}1&,\quad\boldsymbol w^T\boldsymbol x+b>0\\ \\0&,\quad\boldsymbol w^T\boldsymbol x+b\le0\end{matrix}\right. y=φ(v)=⎩⎨⎧10,wTx+b>0,wTx+b≤0
\qquad 一般地,为了更好地表示线性模型,将感知器模型描述为图 2 2 2 中的表示:
\qquad 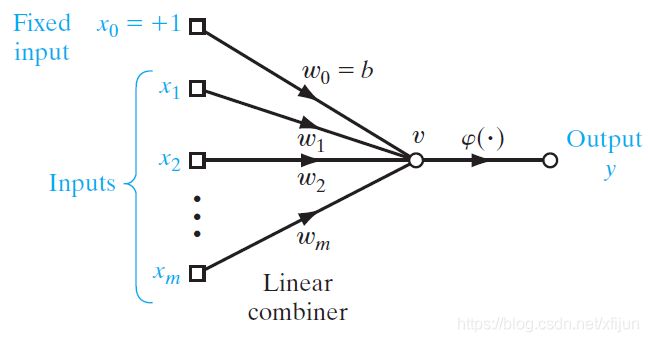
图2From Fig 1.3 《Neural Networks and Learning Machines》
\qquad 如图 2 2 2 所示,将感知器模型中的偏置 b b b 也看作是一个权值 w 0 w_0 w0,那么:
w ^ = [ b , w T ] T = [ w 0 , w 1 , w 2 , ⋯ , w m ] T \qquad\qquad\hat\boldsymbol w=[b,\boldsymbol w^T]^T=[w_0,w_1,w_2,\cdots,w_m]^T w^=[b,wT]T=[w0,w1,w2,⋯,wm]T, w 0 = b w_0=b w0=b
\qquad 为了便于用向量表示线性模型,将训练样本 x = [ x 1 , x 2 , ⋯ , x m ] T \boldsymbol x=[x_1,x_2,\cdots,x_m]^T x=[x1,x2,⋯,xm]T 进行扩展:
x ^ = [ 1 , x T ] T = [ 1 , x 1 , x 2 , ⋯ , x m ] T \qquad\qquad\hat\boldsymbol x=[1,\boldsymbol x^T]^T=[1,x_1,x_2,\cdots,x_m]^T x^=[1,xT]T=[1,x1,x2,⋯,xm]T, x 0 = 1 x_0=1 x0=1
\qquad 因此,图 2 2 2 中的感知器模型可以表示为:
( 1 ) \qquad(1) (1) 线性组合器的输出:
v = w T x + b = w ^ T x ^ \qquad\qquad v=\boldsymbol w^T\boldsymbol x+b=\hat\boldsymbol w^T\hat\boldsymbol x v=wTx+b=w^Tx^
( 2 ) \qquad(2) (2) 感知器的输出:
y = φ ( v ) = { 1 , w ^ T x ^ > 0 0 , w ^ T x ^ ≤ 0 \qquad\qquad y=\varphi(v)=\left\{\begin{matrix}1&,\quad\hat\boldsymbol w^T\hat\boldsymbol x>0\\ \\0&,\quad\hat\boldsymbol w^T\hat\boldsymbol x\le0\end{matrix}\right. y=φ(v)=⎩⎨⎧10,w^Tx^>0,w^Tx^≤0
【注】为了方便表示,本文后续部分直接使用 x \boldsymbol x x 代替 x ^ \hat\boldsymbol x x^,用 w \boldsymbol w w 代替 w ^ \hat\boldsymbol w w^
\qquad
2. 几何意义
- 线性可分的情况——图 3 ( a ) 3(a) 3(a)
\qquad 以输入样本 x = [ x 1 , x 2 ] T ∈ R 2 \boldsymbol x=[x_1,x_2]^T\in R^2 x=[x1,x2]T∈R2 为例,在图 3 ( a ) 3(a) 3(a) 中有 4 4 4 个训练样本: x 1 = [ 0 , 0 ] T , x 2 = [ 1 , 0 ] T , x 3 = [ 1 , 1 ] T , x 4 = [ 0 , 1 ] T \boldsymbol x_1=[0,0]^T,\boldsymbol x_2=[1,0]^T,\boldsymbol x_3=[1,1]^T,\boldsymbol x_4=[0,1]^T x1=[0,0]T,x2=[1,0]T,x3=[1,1]T,x4=[0,1]T,其中 x 1 ∈ ℓ 1 \boldsymbol x_1\in\ell_1 x1∈ℓ1,其余样本属于 ℓ 2 \ell_2 ℓ2。
\qquad 感知器的参数 w = [ b , w 1 , w 2 ] T \boldsymbol w=[b,w_1,w_2]^T w=[b,w1,w2]T 实际上是在 R 2 R^2 R2 中确定了一条直线,如图 3 ( a ) 3(a) 3(a) 所示,能够将正例和负例进行区分的直线并不只有一种选择。
\qquad 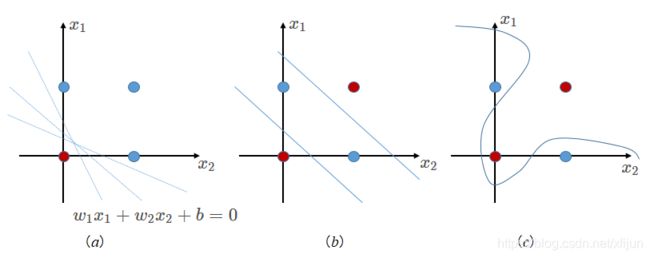
图3感知器模型的几何意义(线性可分、线性不可分)
- 线性不可分的情况——图 3 ( b ) , ( c ) 3(b),(c) 3(b),(c) “异或”问题
\qquad 异或问题无法使用 1 1 1 条直线(分类面)来实现,或者在图 3 ( b ) 3(b) 3(b) 中使用 2 2 2 条直线来区分,或者使用图 3 ( c ) 3(c) 3(c) 中的不规则分类面。
\qquad 图 3 ( b ) 3(b) 3(b) 中使用 2 2 2 条直线实现对数据集的分类,实际上就是采用多层感知器 ( m u l t i l a y e r p e r c e p t r o n , M L P ) (multilayer \ perceptron,MLP) (multilayer perceptron,MLP) 的结构来实现。
\qquad
3. 感知器模型的训练
\qquad 感知器的训练过程,就是为了确定模型的参数 { b , w 1 , w 2 , ⋯ , w m } \{b,w_1,w_2,\cdots,w_m\} {b,w1,w2,⋯,wm}。以图 4 4 4 为例,也就是为了确定 R 2 R^2 R2 中的某条直线的参数 { b , w 1 , w 2 } \{b,w_1,w_2\} {b,w1,w2}。
\qquad 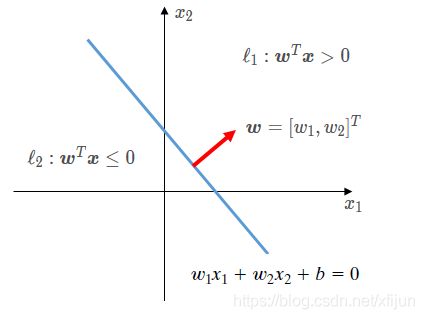
图4感知器的作用是,确定 R 2 R^2 R2 中的分界面(直线)将 ℓ 1 \ell_1 ℓ1 和 ℓ 2 \ell_2 ℓ2 分隔开
\qquad 线性组合器的输出: v = w T x v=\boldsymbol w^T\boldsymbol x v=wTx
\qquad 感知器的(实际)输出值: y = φ ( v ) = { 1 , w T x > 0 ⟹ x ∈ ℓ 1 0 , w T x ≤ 0 ⟹ x ∈ ℓ 2 y=\varphi(v)=\left\{\begin{matrix}1&,\boldsymbol w^T\boldsymbol x>0&\Longrightarrow\boldsymbol x\in\ell_1\\ \\0&,\boldsymbol w^T\boldsymbol x\le0&\Longrightarrow\boldsymbol x\in\ell_2\end{matrix}\right. y=φ(v)=⎩⎨⎧10,wTx>0,wTx≤0⟹x∈ℓ1⟹x∈ℓ2
\qquad 考虑训练样本集:
{ x n , t n } ∣ n = 1 N , x n ∈ R m \qquad\qquad\{\boldsymbol x_n,t_n\}\big |_{n=1}^{N},\boldsymbol x_n\in R^m {xn,tn}∣∣n=1N,xn∈Rm,其中 t n ∈ { 0 , 1 } t_n\in\{0,1\} tn∈{0,1} 为(期望输出的)目标值
\qquad\qquad 对于训练样本 x n \boldsymbol x_n xn,其目标值 t n = { 1 , x n ∈ ℓ 1 0 , x n ∈ ℓ 2 t_n=\left\{\begin{matrix}1&,\boldsymbol x_n\in\ell_1\\ \\0&,\boldsymbol x_n\in\ell_2\end{matrix}\right. tn=⎩⎨⎧10,xn∈ℓ1,xn∈ℓ2
\qquad
\qquad 训练规则基于“误差修正学习”:
w n e w = w o l d − η ( y n − t n ) x n \qquad\qquad\qquad\boldsymbol w^{new}=\boldsymbol w^{old}-\eta(y_n-t_n)\boldsymbol x_n wnew=wold−η(yn−tn)xn, 其中 η \eta η 为学习率
(1)若感知器的输出值 y n y_n yn 与目标值 t n t_n tn 一致时,说明分类面正确区分了当前的训练样本,不需要改变当前分类面,无需调整权值, w n e w = w o l d \boldsymbol w^{new}=\boldsymbol w^{old} wnew=wold
(2)若感知器的输出值 y n y_n yn 与目标值 t n t_n tn 不一致,说明分类面错误区分了当前的训练样本,需要调整权值的大小,来改变分类面的方向,使得当前样本 x n \boldsymbol x_n xn 能够被正确划分
\qquad 考虑具体样本时的“误差修正学习”规则:
- 当训练样本 x n ∈ ℓ 1 ( t n = 1 ) \boldsymbol x_n\in \ell_1\ (t_n=1) xn∈ℓ1 (tn=1) 被送入感知器
⟶ \quad\longrightarrow ⟶ 若输出值 y n = 1 y_n=1 yn=1(判定 x n ∈ ℓ 1 \boldsymbol x_n\in \ell_1 xn∈ℓ1,无误差),权值不会发生改变 w n e w = w o l d \boldsymbol w^{new}=\boldsymbol w^{old} wnew=wold
⟶ \quad\longrightarrow ⟶ 若输出值 y n = 0 y_n=0 yn=0(判定 x n ∈ ℓ 2 \boldsymbol x_n\in \ell_2 xn∈ℓ2,有误差),权值更新为 w n e w = w o l d + η x n \boldsymbol w^{new}=\boldsymbol w^{old}+\eta\boldsymbol x_n wnew=wold+ηxn
\qquad 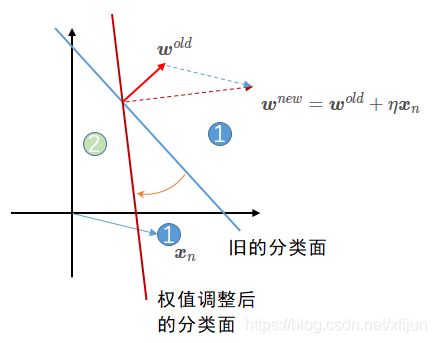
图5权值更新公式 w n e w = w o l d + η x n \boldsymbol w^{new}=\boldsymbol w^{old}+\eta\boldsymbol x_n wnew=wold+ηxn 中取 “ + ” “+” “+” 号的解释【当训练样本 x n \boldsymbol x_n xn 被错误划分】
(1)当训练样本 x n ∈ ℓ 1 \boldsymbol x_n\in \ell_1 xn∈ℓ1 被(旧的)蓝色分类面错误划分,取 “ + ” “+” “+” 号调整权值,才能让旧的分类面旋转到能够正确划分 x n \boldsymbol x_n xn 的红色分类面的方向
(2)训练过程中,学习率 η \eta η 决定了权值变化的幅度(图中为 η = 1 \eta=1 η=1)
(3)已经正确划分的样本不会改变权值,训练过程只会针对图中 x n \boldsymbol x_n xn 样本,通过一步步调整 η x n \eta\boldsymbol x_n ηxn(蓝色虚线向量) 来实现正确划分
- 当训练样本 x n ∈ ℓ 2 ( t n = 0 ) \boldsymbol x_n\in \ell_2\ (t_n=0) xn∈ℓ2 (tn=0) 被送入感知器
⟶ \quad\longrightarrow ⟶ 若输出值 y n = 0 y_n=0 yn=0(判定 x n ∈ ℓ 2 \boldsymbol x_n\in \ell_2 xn∈ℓ2,无误差),权值不会发生改变 w n e w = w o l d \boldsymbol w^{new}=\boldsymbol w^{old} wnew=wold
⟶ \quad\longrightarrow ⟶ 若输出值 y n = 1 y_n=1 yn=1(判定 x n ∈ ℓ 1 \boldsymbol x_n\in \ell_1 xn∈ℓ1,有误差),权值更新为 w n e w = w o l d − η x n \boldsymbol w^{new}=\boldsymbol w^{old}-\eta\boldsymbol x_n wnew=wold−ηxn
\qquad 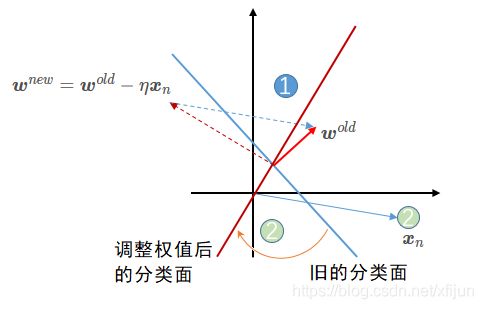
图6权值更新公式 w n e w = w o l d − η x n \boldsymbol w^{new}=\boldsymbol w^{old}-\eta\boldsymbol x_n wnew=wold−ηxn 中取 “ + ” “+” “+” 号的解释【当训练样本 x n \boldsymbol x_n xn 被错误划分】
(1)当训练样本 x n ∈ ℓ 2 \boldsymbol x_n\in \ell_2 xn∈ℓ2 被(旧的)蓝色分类面错误划分,取 “ − ” “-” “−” 号调整权值,才能让旧的分类面旋转到能够正确划分 x n \boldsymbol x_n xn 的红色分类面的方向
(2)训练过程中,学习率 η \eta η 决定了权值变化的幅度(图中为 η = 1 \eta=1 η=1)
(3)已经正确划分的样本不会改变权值,训练过程只会针对图中 x n \boldsymbol x_n xn 样本,通过一步步调整 η x n \eta\boldsymbol x_n ηxn(蓝色虚线向量) 来实现正确划分
\qquad
4. 批处理训练过程
4.1 训练数据的规范化
\qquad 由图 4 4 4,假设分类面 w T x + b = 0 \boldsymbol w^T\boldsymbol x+b=0 wTx+b=0 可以实现正确的分类。那么对于训练样本 x n \boldsymbol x_n xn 而言,如果 w T x n > 0 \boldsymbol w^T\boldsymbol x_n>0 wTxn>0,则 x n ∈ ℓ 1 \boldsymbol x_n\in\ell_1 xn∈ℓ1,如果 w T x n < 0 \boldsymbol w^T\boldsymbol x_n<0 wTxn<0,则 x n ∈ ℓ 2 \boldsymbol x_n\in\ell_2 xn∈ℓ2。
\qquad 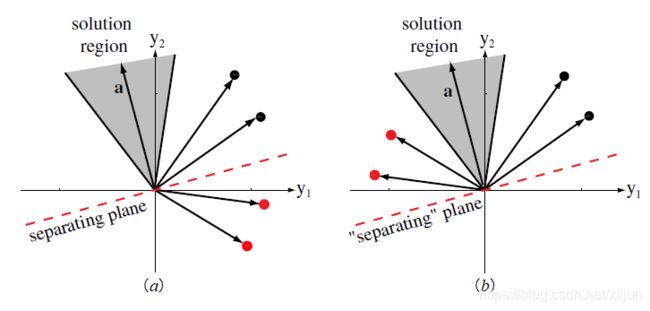
图7训练数据的规范化过程【取自《模式分类》Fig 5.8】
图 (a) 为原始训练数据,黑色训练样本满足 w T x 1 > 0 \boldsymbol w^T\boldsymbol x_1>0 wTx1>0,红色训练样本满足 w T x 2 < 0 \boldsymbol w^T\boldsymbol x_2<0 wTx2<0
图 (b) 为规范化后的数据,红色点取反后,满足 w T ( − x 2 ) > 0 \boldsymbol w^T(-\boldsymbol x_2)>0 wT(−x2)>0
\qquad 训练数据的规范化 ( n o r m a l i z a t i o n ) (normalization) (normalization) 操作可以简化训练过程的描述:
\qquad (1)考虑 x ∈ ℓ 1 \boldsymbol x\in\ell_1 x∈ℓ1 类中训练数据满足 w T x > 0 \boldsymbol w^T\boldsymbol x>0 wTx>0
\qquad (2)将 x ∈ ℓ 2 \boldsymbol x\in\ell_2 x∈ℓ2 类中训练数据取反: w T x < 0 ⟹ w T ( − x ) > 0 \boldsymbol w^T\boldsymbol x<0\Longrightarrow\boldsymbol w^T(-\boldsymbol x)>0 wTx<0⟹wT(−x)>0
\qquad (3)此时,寻找权向量 w \boldsymbol w w 只需要针对新的数据集 ℓ = ℓ 1 ∪ { − ℓ 2 } \bold\ell=\ell_1\cup\{-\ell_2\} ℓ=ℓ1∪{−ℓ2} ,计算 w T x > 0 , x ∈ ℓ \boldsymbol w^T\boldsymbol x>0,\boldsymbol x\in\bold\ell wTx>0,x∈ℓ 即可。
\qquad
4.2 批处理感知器算法
\qquad 定义感知器代价函数:
J ( w ) = ∑ x ∈ X ( − w T x ) \qquad\qquad\qquad J(\boldsymbol w)=\displaystyle\sum_{\boldsymbol x\in \mathcal X}(-\boldsymbol w^T\boldsymbol x) J(w)=x∈X∑(−wTx)
\qquad 其中, X \mathcal X X 表示被错误划分的训练样本集。
\qquad 若 x ∈ ℓ 1 \boldsymbol x\in\ell_1 x∈ℓ1 被错分,那么 w T x < 0 \boldsymbol w^T\boldsymbol x<0 wTx<0;若 x ∈ ℓ 2 \boldsymbol x\in\ell_2 x∈ℓ2 被错分,那么 w T ( − x ) < 0 \boldsymbol w^T(-\boldsymbol x)<0 wT(−x)<0 。因此,选择 ∑ x ∈ X ( − w T x ) \sum_{\boldsymbol x\in \mathcal X}(-\boldsymbol w^T\boldsymbol x) ∑x∈X(−wTx) 作为代价函数,被错分的训练样本越多,代价函数的值就越大。
\qquad 如果 X \mathcal X X 为空集,则表明所有训练样本都被正确分类,代价函数的值就越小。
\qquad 采用梯度下降法求解:
∇ J ( w ) = ∂ J ( w ) ∂ w = ∑ x ∈ X ( − x ) \qquad\qquad \nabla J(\boldsymbol w)=\dfrac{\partial J(\boldsymbol w)}{\partial \boldsymbol w}=\displaystyle\sum_{\boldsymbol x\in \mathcal X}(-\boldsymbol x) ∇J(w)=∂w∂J(w)=x∈X∑(−x)
w n e w = w o l d − η ∇ J ( w ) \qquad\qquad \boldsymbol w^{new}=\boldsymbol w^{old}-\eta\nabla J(\boldsymbol w) wnew=wold−η∇J(w)
\qquad 因此,迭代公式为:
w n e w = w o l d + η ∑ x ∈ X x \qquad\qquad \boldsymbol w^{new}=\boldsymbol w^{old}+\eta\displaystyle\sum_{\boldsymbol x\in \mathcal X}\boldsymbol x wnew=wold+ηx∈X∑x
\qquad
实现代码
import numpy as np
import matplotlib.pyplot as plt
def singleperceptron(xhat,target,eta,mode='seq'):
iteration = 0
flag = 1
if mode=='seq':
weight = np.random.random(xhat.shape[1])
y = np.zeros((len(xhat),1))
while flag:
# sequential
for i in range(len(xhat)):
tmp = np.dot(weight,xhat[i,:])
if tmp > 0:
y[i] = 1
else:
y[i] = 0
weight = weight - eta*(y[i]-target[i])*xhat[i,:]
print(weight)
iteration = iteration + 1
if np.sum(np.abs(y-target))==0:#此处的迭代终止条件只针对线性可分数据
flag = 0
if mode=='batch':
weight = np.random.random((xhat.shape[1],1))
xhat1 = xhat*np.where(target>0,1,-1)
print(weight.flatten())
while flag:
# batch
y1 = np.dot(xhat,weight)
y1 = np.where(y1>0,1,0)
t = np.dot(xhat1.T, np.abs(y1-target))
weight += eta*t
print(weight.flatten())
iteration = iteration + 1
if np.sum(t)==0:#此处的迭代终止条件只针对线性可分数据
flag = 0
weight = weight.flatten()/np.sum(weight)
return weight
def gen_lineardata(weight,interval):
y = -(weight[0]*interval + weight[2])/weight[1]
return y
def halfmoon(rad, width, dist, n_samp):
if n_samp%2 != 0:
n_samp += 1
data = np.zeros((3,n_samp))
rd = np.random.random((2,n_samp//2))
radius = (rad-width//2) + width*rd[0,:]
theta = np.pi*rd[1,:]
x1 = radius*np.cos(theta)
y1 = radius*np.sin(theta) + dist/2
label1 = np.ones((1,len(x1))) # label= 1 for Class 1
x2 = radius*np.cos(-theta) + rad
y2 = radius*np.sin(-theta) - dist/2
label2= np.zeros((1,len(x2))) # label= 0 for Class 2
data[0,:]=np.concatenate([x1,x2])
data[1,:]=np.concatenate([y1,y2])
data[2,:]=np.concatenate([label1,label2],axis=1)
shuffle_seq = np.random.permutation(np.arange(n_samp))
data_shuffle = data[:,shuffle_seq]
return data,data_shuffle
if __name__ == "__main__":
# dataset1: halfmoon
tnum = 8000
data,data_shuffle = halfmoon(20,15,3,tnum)
pos_data = data[:,0:tnum//2]
neg_data = data[:,tnum//2:tnum]
training_data = data_shuffle.T
tmp1 = training_data[0:tnum,0:2]
tmp2 = np.ones((tnum,1))
xhat = np.concatenate((tmp1,tmp2),axis=1)
target = training_data[0:tnum,2:]
interval = np.linspace(-30,50,100)
# dataset2: or
# data = np.array([[0,0],[0,1],[1,1],[1,0]])
# pos_data = data[0:1,:].T
# neg_data = data[1:,:].T
# target = np.array([1,0,0,0]).reshape(4,1)
# xhat = np.concatenate((data,np.ones((4,1))),axis=1)
# interval = np.linspace(-0.2,0.6,100)
# main
weight = singleperceptron(xhat,target,0.2)
print('sequential:',weight)
y = gen_lineardata(weight,interval)
plt.figure(1)
plt.plot(interval,y,'k')
plt.plot(pos_data[0,:],pos_data[1,:],'bo',markerSize=1)
plt.plot(neg_data[0,:],neg_data[1,:],'ro',markerSize=1)
plt.title('sequential')
weight = singleperceptron(xhat,target,0.2,'batch')
print('batch:',weight)
y = gen_lineardata(weight,interval)
plt.figure(2)
plt.plot(interval,y,'k')
plt.plot(pos_data[0,:],pos_data[1,:],'bo',markerSize=1)
plt.plot(neg_data[0,:],neg_data[1,:],'ro',markerSize=1)
plt.title('batch')
plt.show()
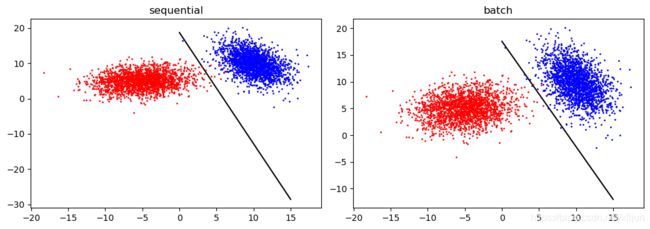
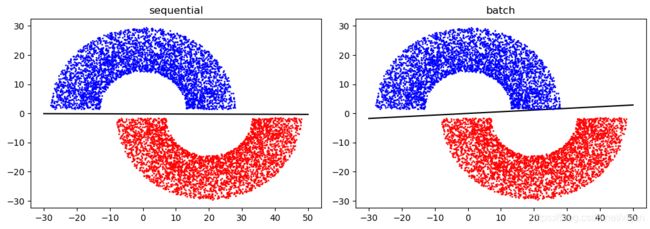
某一次运行结果
(1)半月形数据
sequential模式: [ w 1 , w 2 , b ] = [w_1,w_2,b]= [w1,w2,b]= [0.01727369 5.59047961 0.9740486 ]
batch模式: [ w 1 , w 2 , b ] = [w_1,w_2,b]= [w1,w2,b]= [-0.06142 1.06444655 -0.00302655]
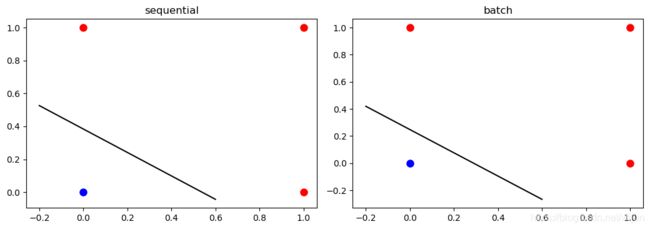
(2)OR数据:
sequential模式: [ w 1 , w 2 , b ] = [w_1,w_2,b]= [w1,w2,b]= [-0.22742997 -0.31955376 0.1226006 ]
batch模式: [ w 1 , w 2 , b ] = [w_1,w_2,b]= [w1,w2,b]= [ 0.53262345 0.62096392 -0.15358737]
 (3)线性不可分数据
(3)线性不可分数据