GloVe

背景介绍

word2vec最大的问题是基于局部窗口而训练出来的词向量是没有全局性的(一定程度上)，还有一种利用全局矩阵分解形式训练的词向量，但这种方法在词对推理任务上表现不是很好。
GloVe采用了词频共现的模型来训练词向量，即基于全局词汇共现的统计信息来学习词向量，从而将统计信息和局部上下文窗口两种方法的优点结合起来。出自论文《GloVe- Global Vectors for Word Representation》
参考：GloVe详解

GloVe模型讲解

原理

在日常阅读中，我们会发现一些词汇经常是一起出现的，比如当描述一件衣服的颜色时，我们会发现衣服的颜色（红色、黑色等）会和颜色这个词一块出现；形容冰块时我们常常用固体来形容；形容水蒸气时我们常常用气体来形容。也就是说经常一起出现的词汇组，当其中一个词出现时，另一个词在一个句子中出现的概率也很大，而其他不相关的单词出现的概率就很小，所以我们可以用共现矩阵的概率比值来区分词。
如下图,我们使用冰块和蒸汽来描述固体、气体、水和时尚四个词。

当K=solid时：
$P\left(solid|ice\right)$/$P\left(solid|steam\right)$为8.9，远大于1，表示固体和冰块共现的概率相比较与蒸汽更大。
当K=gas时：
$P\left(gas|ice\right)$/$P\left(gas|steam\right)$为0.085，远小于1，表示气体和冰块共现的概率相比较与蒸汽更小。
当K=water时：
$P\left(water|ice\right)$/$P\left(water|steam\right)$为1.39，接近1，表示在这个语料库中，水与冰块共现的概率相比较于蒸汽来说只是多一点，或者说水和冰块、蒸汽都相近。
当K=fashion时：
$P\left(fashionr|ice\right)$/$P\left(fashion|steam\right)$为0.96，几乎等于1，表示在这个语料库中，时尚与冰块共现的概率相比较于蒸汽来说相近或者说时尚和冰块、蒸汽都不相关；而且看单独的比值，时尚与这两个词共现的概率都很小。

GloVe模型

GloVe模型首先根据语料库构建一个共现矩阵X，矩阵中的每一元素$X_{ij}$代表了在特定窗口下单词$X_i$和上下文单词$X_j$共现的次数；另外GloVe还提出了一个衰减函数的概念：两个单词共现的次数越多，那么其权重就应该越大，表现为：两个单词在上下文窗口的距离为d，权重decay=1/d，距离越远的两个单词所占总计数的权重就越小。
GloVe是构建词向量和共现矩阵之间的近似关系训练词向量的，其关系为：

其中$W_i^T$和$W_j$是我们要求取得词向量。
另外损失函数（均方损失函数）为：

$f(X_{ij})$为衰减函数。

GloVe模型细节

根据上图，由于我们可以用共现矩阵的概率比值来区分词，即可以根据$P\left(K|ice\right)$/$P\left(K|steam\right)$来判断单词K和ice更接近还是和steam更接近。也就是说，我们可以通过概率的比例比较而不是单词K和上下文单词共现的概率去学习词向量，这种方法更好，即可以全局地学习词向量，也可以区分单词间的不同。
构建词向量和共现矩阵之间的近似关系公式推导过程：
首先我们建立公式：
$$F(w_i,w_j,\widetilde{w_k})=\frac{P_{ik}}{P_{jk}},\text{\hspace{1em}(1)}$$
其中$w_i$、$w_j$为上下文窗口单词向量，$\widetilde{w_k}$是目标向量。$P_{ik}$、$P_{jk}$分别为单词K对单词i、j的共现概率。
其次，由于向量空间是线性结构的，所以为了表达出两个概率的比例差异，我们在函数F的形式上做了点改变，即：
$$F(w_i-w_j,\widetilde{w_k})=\frac{P_{ik}}{P_{jk}},\text{\hspace{1em}(2)}$$
再者，公式2的右侧是一个标量值，而函数F内都是向量值，我们可以将其转换为两个向量的内积形式：
$$F((w_i-w_j{)}^T\widetilde{w_k})=\frac{P_{ik}}{P_{jk}},\text{\hspace{1em}(3)}$$
然后我们令F=exp，有如下的推导过程：

我们可以得知：EXP（$w_i^T$$\widetilde{w_k}$）=$P_{ik}$,其中i为上下文窗口任一单词，k为目标单词。
EXP（$w_i^T$$\widetilde{w_k}$）=$P_{ik}$，由于$P_{ik}$=$\frac{P_{ik}}{P_{jk}}$,那么：
$$w_i^T\widetilde{w_k}=\log (P_{ik})=\log (X_{ik})–\log (X_i),\text{\hspace{1em}(4)}$$
公式4是不满足对称性的，而且这个$\log (X_i)$是跟K独立的，它只跟i相关，于是我们可以将$w_i$替换为$b_i$，即一个偏差项，那么：
$$w_i^T\widetilde{w_k}+b_i=\log (X_{ik}),\text{\hspace{1em}(5)}$$
最后由于公式5还不满足不对称性，我们针对$w_k$增加一个偏差项$b_k$，从而得出我们要训练的模型关系公式：
$$w_i^T\widetilde{w_k}+b_i+b_k=\log (X_{ik})$$

损失函数细节

损失函数如上图所示：
右边平方里面就是计算出来的$X_{ij}$的比值和真实的$X_{ij}$之间的差值。

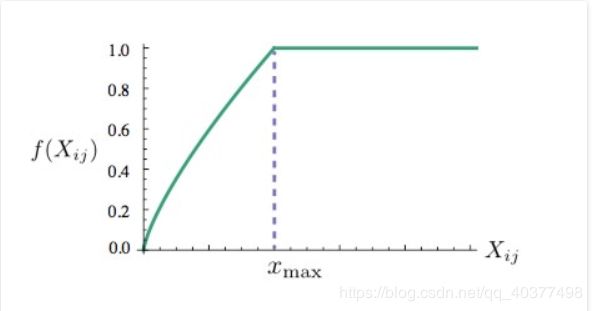
f（$X_{ij}$）为权重函数。在一个语料库中，很多单词共现的次数很多，那么这些单词组的权重要大于其他很少一起出现的单词，就比如上面冰块和固体的权重要大于冰块和气体的权重，所以这个函数是非递减函数；同时，权重也不能过大，因为s、the、are这些词的影响（出现次数太多了）。所以设置该权重达到一定程度后就不再增加；另外当两个单词没有在一起出现，即$X_{ij}=0$时，权重为0，那么不参加训练。
那么f（$X_{ij}$）的形式为:

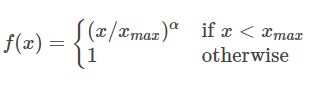
函数图像为：

代码

class glove_model(nn.Module):
    def __init__(self,vocab_size,embed_size,x_max,alpha):
        super(glove_model, self).__init__()
        self.vocab_size = vocab_size
        self.embed_size = embed_size
        self.x_max = x_max
        self.alpha = alpha
        self.w_embed = nn.Embedding(self.vocab_size,self.embed_size).type(torch.float64)

        self.w_bias = nn.Embedding(self.vocab_size,1).type(torch.float64)

        self.v_embed = nn.Embedding(self.vocab_size, self.embed_size).type(torch.float64)

        self.v_bias = nn.Embedding(self.vocab_size, 1).type(torch.float64)
    def forward(self, w_data,v_data,labels):
        w_data_embed = self.w_embed(w_data)
        w_data_bias = self.w_bias(w_data)
        v_data_embed = self.v_embed(v_data)
        v_data_bias = self.v_bias(v_data)
        weights = torch.pow(labels/self.x_max,self.alpha)
        weights[weights>1]=1
        loss = torch.mean(weights*torch.pow(torch.sum(w_data_embed*v_data_embed,1)+w_data_bias+v_data_bias-
                                 torch.log(labels),2))
        return loss