何为跳表?
跳表是一个随机化的数据结构,实质就是一种可以进行二分查找的有序链表。
跳表在原有的有序链表上面增加了多级索引,通过索引来实现快速查找。
跳表不仅能提高搜索性能,同时也可以提高插入和删除操作的性能。
跳表详解
有序链表
考虑一个有序链表,我们要查找3、7、17这几个元素,我们只能从头开始遍历链表,直到查找到元素为止。
上述这个链表是有序的,但是不能使用二分查找,是不是很捉急?(P.S.数组可以实现二分查找)
那么,有没有什么方法可以实现有序链表的二分查找呢?
答案是肯定的,那就是我们将要介绍的这种数据结构——跳表。
跳表的演进
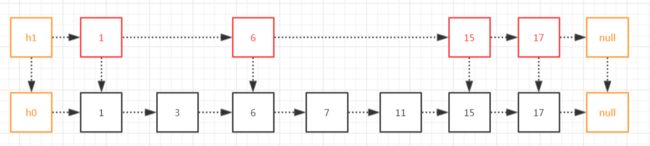
我们把一些节点从有序表中提取出来,缓存一级索引,就组成了下面这样的结构:
现在,我们要查找17这个元素是不是要快很多呢?
我们只要从一级索引往后遍历即可,只需要经过1、6、15、17这几个元素就可以找到17了。
那么,我们要查找11这个元素呢?
我们从一级索引的1开始,向右到6,再向右发现是15,它比11大,此路不通,从6往下走,再从下面的6往右走,到7,再到11。
同样地,一级索引也可以往上再提取一层,组成二级索引,如下:
![]()
这时候我们再查找17这个元素呢?
只需要经过6、15、17这几个元素就可以找到17了。
这基本上就是跳表的核心思想了,其实这也是一个“空间换时间”的算法,通过向上提取索引增加了查找的效率。
跳表的插入
上面讲的都是跳表的查询,那么,该如何向跳表中插入元素呢?
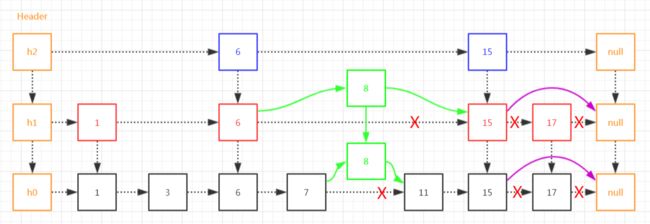
比如,我们要向上面这个跳表添加一个元素8。
首先,我们先根据投硬币的方式,决定8这个元素要占据的层数,没错就是扔硬币,是不是很好玩儿^^
比如,层数level=2。
然后,找到8这个元素在下面两层的前置节点。
接着,就是链表的插入元素操作了,比较简单。
最后,就像下面这样:
跳表的删除
查询、插入元素都讲了,下面我们就来说说怎么删除元素。
首先,找到各层中包含元素x的节点。
然后,使用标准的链表删除元素的方法删除即可。
比如,要删除17这个元素。
标准化的跳表
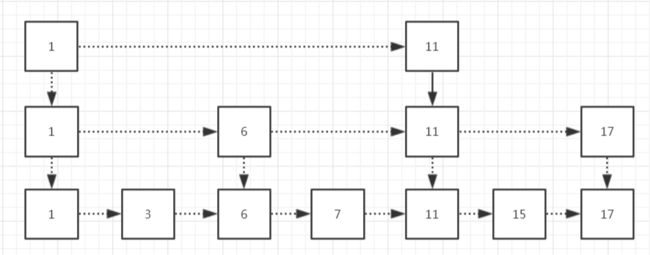
上面举的例子是完全随机的跳表,那么,如果我们每两个元素提取一个元素作为上一级的索引会怎么样呢?
这是不是很像平衡二叉树,现在这颗树元素比较少,可能不太明显,我们来看个元素个数多的情况。
可以看到,上一级元素的个数是下一级的一半,这样每次减少一半,就很接近平衡二叉树了。
时间复杂度
我们知道单链表查询的时间复杂度为O(n),而插入、删除操作需要先找到对应的位置,所以插入、删除的时间复杂度也是O(n)。
那么,跳表的时间复杂度是多少呢?
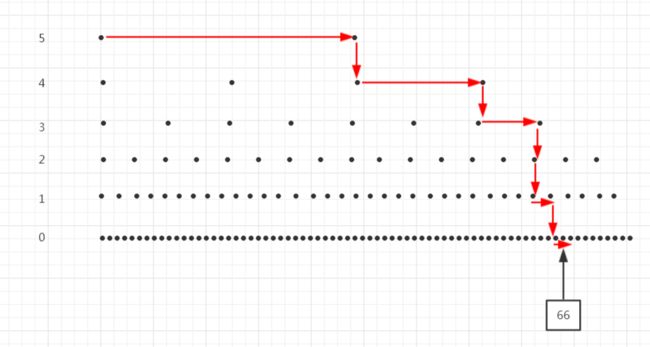
如果按照标准的跳表来看的话,每一级索引减少k/2个元素(k为其下面一级索引的个数),那么整个跳表的高度就是(log n)。
学习过平衡二叉树的同学都知道,它的时间复杂度与树的高度成正比,即O(log n)。
所以,这里跳表的时间复杂度也是O(log n)。(这里不一步步推倒了,只要记住,查询时每次减少一半的元素的时间复杂度都是O(log n),比如二叉树的查找、二分法查找、归并排序、快速排序)
空间复杂度
我们还是以标准的跳表来分析,每两个元素向上提取一个元素,那么,最后额外需要的空间就是:
n/2 + (n/2)^2 + (n/2)^3 + ... + 8 + 4 + 2 = n - 2
所以,跳表的空间复杂度是O(n)。
总结
(1)跳表是可以实现二分查找的有序链表;
(2)每个元素插入时随机生成它的level;
(3)最低层包含所有的元素;
(4)如果一个元素出现在level(x),那么它肯定出现在x以下的level中;
(5)每个索引节点包含两个指针,一个向下,一个向右;
(6)跳表查询、插入、删除的时间复杂度为O(log n),与平衡二叉树接近;
彩蛋
为什么Redis选择使用跳表而不是红黑树来实现有序集合?
首先,我们来分析下Redis的有序集合支持的操作:
1)插入元素
2)删除元素
3)查找元素
4)有序输出所有元素
5)查找区间内所有元素
其中,前4项红黑树都可以完成,且时间复杂度与跳表一致。
但是,最后一项,红黑树的效率就没有跳表高了。
在跳表中,要查找区间的元素,我们只要定位到两个区间端点在最低层级的位置,然后按顺序遍历元素就可以了,非常高效。
而红黑树只能定位到端点后,再从首位置开始每次都要查找后继节点,相对来说是比较耗时的。
此外,跳表实现起来很容易且易读,红黑树实现起来相对困难,所以Redis选择使用跳表来实现有序集合。
欢迎关注我的公众号“彤哥读源码”,查看更多源码系列文章, 与彤哥一起畅游源码的海洋。