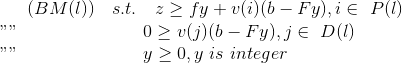运筹学读书笔记---Benders Decomposition

1、前言

最近在读这本厚厚的运筹学书籍，发现这本书写的真的好。大规模优化方法系列，有个叫benders分解的算法，之前只是听过名字，不懂具体原理。仔细啃了一下，还是很有意思的。

2、分解策略

                              

      

如果y值固定，上述问题就变成一个线性规划问题。因此，在第l次迭代时。选取部分整数决策变量y(l)并固定相应的值，从而将整数规划转化为只包含连续决策变量的问题，如下所示：

                      

由BP(l)的对偶问题得到第l次迭代的Benders的子问题。

                     

当求解对偶子问题(BD(l))时，可能会出现两种情形：子问题的最优解对应一个极点v(i)或者子问题无界，最优解对应一个极方向v(j)。因此，在benders主问题求解变量y的整数规划模型如下形式：

                        

当考虑所有的极点和极方向时，BM问题一定可以找到最优的y，但此时的模型可能包含指数级别的数量的极点和大量的极方向。和列生成算法类似，限制主问题只考虑当前迭代时生成的极点和极方向，每次迭代会逐步添加新的极点和极方向。

                     

3、最优性原理

如果第次迭代模型的值小于等于上一次迭代得到的限制主问题最优目标函数值小,即

因为的约束比的约束少，所以是的上界，即。随着迭代过程中约束条件越来越多，的值应该是增加的，所以是的下界，即。所以每次迭代中会有,一旦,迭代达到终止条件。

4、整体流程

第0步：初始化。。

第1步：Benders子问题求解。若目标函数值有界限，得到极点，进入第2步。若目标函数无界，得到极方向，进入第3步。

第2步：算法终止判断。如果停止，得到,进而求解。

第3步：限制主问题更新，将新得到的极点和极方向以约束条件的形式添加到zhong。

第4步：主问题求解。求解得到和目标函数z。，返回第1步。

5、基于Gurobi模型构建

import gurobipy as gp
from gurobipy import GRB
import numpy as np

class Benders_Example(object):
    def __init__(self,i_num,j_num):
        self.j_num = j_num
        self.i_num = i_num
        self.f = [400, 250, 300]
        self.d = [75, 90, 81, 26, 57]
        self.cost = [[4, 7, 3, 12, 15],
                     [13, 11, 17, 9, 19],
                     [8, 12, 10, 7, 5]]

    def build_model(self):
        model = gp.Model("Benders")
        x_ij = model.addVars(self.i_num,self.j_num,vtype=GRB.CONTINUOUS,obj=self.cost,lb=0,ub=GRB.INFINITY,name="x")
        y_i = model.addVars(self.i_num,vtype=GRB.BINARY,obj=self.f,name="y")
        model.modelSense=GRB.MINIMIZE

        #add constr
        model.addConstrs((x_ij.sum(i,"*") <= y_i[i] * sum(self.d) for i in range(self.i_num)),name='c1')

        model.addConstrs((x_ij.sum("*",j) == self.d[j] for j in range(self.j_num)),name='c2')

        model.write("benders.lp")
        model.optimize()
        print("model obj = ",model.objVal)
        for i in range(self.i_num):
            print("y(%d)=%lf" % (i,y_i[i].x))
            for j in range(self.j_num):
                print(x_ij[i,j].x)

6、基于Gurobi实现Benders算法

只是粗略的实现，直接建模型求解和用benders算法求解。代码框架还需要优化，后边有时间再打磨。

github:https://github.com/IELBHJY/OperationsResearch/tree/master/Benders

 

 

 

 

参考资料：本文资料是来自<>