Unity 小球融合 贝塞尔曲线模拟
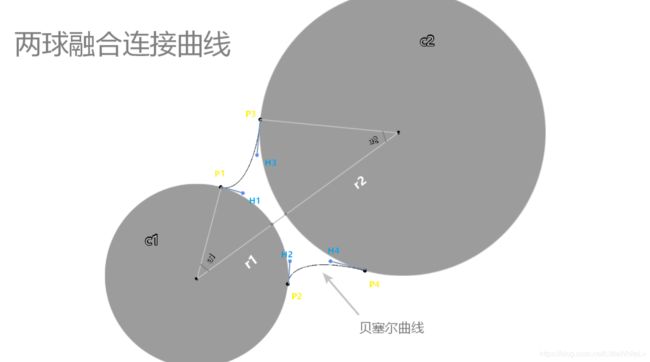
前几天做小球融合,让我陷入困难,后来搜到用贝塞尔曲线模拟中间过渡效果的,但是他们的代码都有显然的和隐藏的错误之处,改了半天都无法达到预期效果,不够直白易懂,但是经过一天的琢磨最后还是搞懂了思路并想到了算法,源码和项目也分享给大家学习,注释很详细,所以我只简单解释思路,示意图:
如图,根据两球的距离设置合适的a1和a2,求出P1,P2,P3,P4的坐标,然后根据圆上切线的方向,自己根据圆的半径和两圆的距离,求出沿切线方向的切点坐标,即可得出绘制贝塞尔曲线的四个坐标点,特判一些特殊情况,加入融合时修改半径的功能即可。不知道核心代码怎么使用的话可以下载项目运行看看。
效果图:
把算法放到processing上运行,效率也很高:
unity2018.4 demo项目:https://pan.baidu.com/s/1u8GF-ziL3C84PDK_0N9Q9A 密码:2333
核心代码:
using UnityEngine;
public class Curve : MonoBehaviour {
public int lineNum; //曲线分段数
public Material line; //材质颜色
public Transform c1, c2; //圆
public Transform p1, p2, p3, p4; //圆上的切点
public Transform h1, h2, h3, h4; //切线延伸方向的点
private Vector2 P1, P2, P3, P4, H1, H2, H3, H4; //8个点坐标
private float initAngle = 40; //初始不相交时的两圆切点相对于各自圆心的夹角
private float tangentLength1, tangentLength2; //切线长度
private float scaleRate = 0.01f; //圆融合时面积变化比例
private void Update() {
Vector2 scale = Metaball(c1.position, c2.position, c1.localScale.x * 2.5f, c2.localScale.x * 2.5f);
SetScale(scale);
}
//计算8点位置
private Vector2 Metaball(Vector2 c1, Vector2 c2, float r1, float r2) {
Vector2 ans = new Vector2();
float dis = Vector2.Distance(c1, c2); //两圆心的距离
if (dis < r1 + r2) { //吸收小圆
ans.x = r1 * (1 - scaleRate); //小圆新半径
ans.y = Mathf.Sqrt(r2 * r2 + r1 * r1 - ans.x * ans.x); //大圆新半径
}
else { //分离,不吸收
ans = new Vector2(r1, r2);
}
float tiltAngle1, tiltAngle2; //两圆心的相对角度
tiltAngle1 = Vector2.Angle(c2 - c1, new Vector2(1, 0)); //angle函数返回夹角绝对值,下一句手动判断正负
if ((c2 - c1).y < 0) tiltAngle1 = -tiltAngle1;
tiltAngle2 = Limit(tiltAngle1 + 180);
float angle1, angle2, angle3, angle4; //四个切点相对于圆心的角度
angle1 = angle2 = angle3 = angle4 = 0;
float tanAngle1, tanAngle2, tanAngle3, tanAngle4; //四个切线方向的角度
if (dis > r1 + r2) { //两圆不相交
angle1 = Limit(tiltAngle1 + initAngle);
angle2 = Limit(tiltAngle1 - initAngle);
angle3 = Limit(tiltAngle2 - initAngle);
angle4 = Limit(tiltAngle2 + initAngle);
tangentLength1 = r1 * dis / 20;
if (tangentLength1 > r1 / 4) tangentLength1 = r1 / 4;
tangentLength2 = r2 * dis / 20;
if (tangentLength2 > r2 / 4) tangentLength2 = r2 / 4;
}
else if (r1 < dis + r2 && r2 < dis + r1) { //两圆相交
float interAngle1, interAngle2; //相交点相对于圆心的角度
interAngle1 = Mathf.Acos((r1 * r1 - r2 * r2 + dis * dis) / (2 * dis * r1)) * Mathf.Rad2Deg; //推导出的公式
interAngle2 = Mathf.Acos((r2 * r2 - r1 * r1 + dis * dis) / (2 * dis * r2)) * Mathf.Rad2Deg;
angle1 = Limit(tiltAngle1 + interAngle1 + initAngle);
angle2 = Limit(tiltAngle1 - interAngle1 - initAngle);
angle3 = Limit(tiltAngle2 - interAngle2 - initAngle);
angle4 = Limit(tiltAngle2 + interAngle2 + initAngle);
tangentLength1 = r1 / 4;
tangentLength2 = r2 / 4;
}
tanAngle1 = Limit(angle1 - 90);
tanAngle2 = Limit(angle2 + 90);
tanAngle3 = Limit(angle3 + 90);
tanAngle4 = Limit(angle4 - 90);
P1 = c1 + new Vector2(Mathf.Cos(angle1 * Mathf.Deg2Rad), Mathf.Sin(angle1 * Mathf.Deg2Rad)) * r1;
P2 = c1 + new Vector2(Mathf.Cos(angle2 * Mathf.Deg2Rad), Mathf.Sin(angle2 * Mathf.Deg2Rad)) * r1;
P3 = c2 + new Vector2(Mathf.Cos(angle3 * Mathf.Deg2Rad), Mathf.Sin(angle3 * Mathf.Deg2Rad)) * r2;
P4 = c2 + new Vector2(Mathf.Cos(angle4 * Mathf.Deg2Rad), Mathf.Sin(angle4 * Mathf.Deg2Rad)) * r2;
H1 = P1 + new Vector2(Mathf.Cos(tanAngle1 * Mathf.Deg2Rad), Mathf.Sin(tanAngle1 * Mathf.Deg2Rad)) * tangentLength1;
H2 = P2 + new Vector2(Mathf.Cos(tanAngle2 * Mathf.Deg2Rad), Mathf.Sin(tanAngle2 * Mathf.Deg2Rad)) * tangentLength1;
H3 = P3 + new Vector2(Mathf.Cos(tanAngle3 * Mathf.Deg2Rad), Mathf.Sin(tanAngle3 * Mathf.Deg2Rad)) * tangentLength2;
H4 = P4 + new Vector2(Mathf.Cos(tanAngle4 * Mathf.Deg2Rad), Mathf.Sin(tanAngle4 * Mathf.Deg2Rad)) * tangentLength2;
/*
P1 = p1.position;
P2 = p2.position;
P3 = p3.position;
P4 = p4.position;
H1 = h1.position;
H2 = h2.position;
H3 = h3.position;
H4 = h4.position;
*/
SetPointPos(P1, P2, P3, P4, H1, H2, H3, H4);
if (r1 < dis + r2 && r2 < dis + r1) { //圆没有互相包含时
DrawCurve();
}
return ans;
}
//设置小球新半径
private void SetScale(Vector2 scale) {
c1.localScale = new Vector3(1, 1, 1) * scale.x / 2.5f;
c2.localScale = new Vector3(1, 1, 1) * scale.y / 2.5f;
}
//限制角度在-180到180之间
private float Limit(float angle) {
if (angle > 180) return angle - 360;
if (angle <= -180) return angle + 360;
return angle;
}
//显示8个点的位置
private void SetPointPos(Vector2 P1, Vector2 P2, Vector2 P3, Vector2 P4, Vector2 H1, Vector2 H2, Vector2 H3, Vector2 H4) {
p1.position = P1;
p2.position = P2;
p3.position = P3;
p4.position = P4;
h1.position = H1;
h2.position = H2;
h3.position = H3;
h4.position = H4;
}
//编辑器界面绘制贝塞尔曲线
private void DrawCurve() {
float x;
Vector2 A, B, C, D;
Vector2[] Mpos = new Vector2[6];
Vector2 last = Vector2.zero;
A = P2;
B = H2;
C = H4;
D = P4;
x = 0;
for (int i = 0; i <= lineNum; i++) {//贝塞尔曲线
Mpos[0] = A + (B - A) * x;
Mpos[1] = B + (C - B) * x;
Mpos[2] = C + (D - C) * x;
Mpos[3] = Mpos[0] + (Mpos[1] - Mpos[0]) * x;
Mpos[4] = Mpos[1] + (Mpos[2] - Mpos[1]) * x;
Mpos[5] = Mpos[3] + (Mpos[4] - Mpos[3]) * x;
if (i != 0) {
Debug.DrawLine(last, Mpos[5], Color.white);
}
x += 1.0f / lineNum;
last = Mpos[5];
}
A = P1;
B = H1;
C = H3;
D = P3;
x = 0;
for (int i = 0; i <= lineNum; i++) {//贝塞尔曲线
Mpos[0] = A + (B - A) * x;
Mpos[1] = B + (C - B) * x;
Mpos[2] = C + (D - C) * x;
Mpos[3] = Mpos[0] + (Mpos[1] - Mpos[0]) * x;
Mpos[4] = Mpos[1] + (Mpos[2] - Mpos[1]) * x;
Mpos[5] = Mpos[3] + (Mpos[4] - Mpos[3]) * x;
if (i != 0) {
Debug.DrawLine(last, Mpos[5], Color.white);
}
x += 1.0f / lineNum;
last = Mpos[5];
}
}
//游戏界面绘制贝塞尔曲线
private void OnPostRender() {
float x;
Vector2 A, B, C, D;
Vector2[] Mpos = new Vector2[6];
Vector2 last = Vector2.zero;
GL.PushMatrix();
GL.LoadPixelMatrix();
line.SetPass(0);
GL.Begin(GL.LINES);
A = P2;
B = H2;
C = H4;
D = P4;
x = 0;
for (int i = 0; i <= lineNum; i++) {//贝塞尔曲线
Mpos[0] = A + (B - A) * x;
Mpos[1] = B + (C - B) * x;
Mpos[2] = C + (D - C) * x;
Mpos[3] = Mpos[0] + (Mpos[1] - Mpos[0]) * x;
Mpos[4] = Mpos[1] + (Mpos[2] - Mpos[1]) * x;
Mpos[5] = Mpos[3] + (Mpos[4] - Mpos[3]) * x;
Vector2 pos = Camera.main.WorldToScreenPoint(Mpos[5]);
if (i == 0) {
GL.Vertex3(pos.x, pos.y, 0);
}
else {
GL.Vertex3(last.x, last.y, 0);
}
GL.Vertex3(pos.x, pos.y, 0);
x += 1.0f / lineNum;
last = pos;
}
GL.End();
GL.Begin(GL.LINES);
A = P1;
B = H1;
C = H3;
D = P3;
x = 0;
for (int i = 0; i <= lineNum; i++) {//贝塞尔曲线
Mpos[0] = A + (B - A) * x;
Mpos[1] = B + (C - B) * x;
Mpos[2] = C + (D - C) * x;
Mpos[3] = Mpos[0] + (Mpos[1] - Mpos[0]) * x;
Mpos[4] = Mpos[1] + (Mpos[2] - Mpos[1]) * x;
Mpos[5] = Mpos[3] + (Mpos[4] - Mpos[3]) * x;
Vector2 pos = Camera.main.WorldToScreenPoint(Mpos[5]);
if (i == 0) {
GL.Vertex3(pos.x, pos.y, 0);
}
else {
GL.Vertex3(last.x, last.y, 0);
}
GL.Vertex3(pos.x, pos.y, 0);
x += 1.0f / lineNum;
last = pos;
}
GL.End();
GL.PopMatrix();
}
}