算法 线段树专题总结（帮助萌新认识线段树）

写在读前：
本文中专题指[kuangbin]线段树专题中前九道，面向已经学习了分治与递归的基础算法，初次认识线段树的萌新，且文中线段树实现方式大多为数组与递归的方式实现，相对易于理解。博客内容包括笔者对线段树的浅薄见解以及九道题目的要点总结；多有不足请大佬们指出。

关于线段树：

笔者对线段树的认识是"一种批量处理数据的高效算法"，是建立在树的数据结构与分治的算法思想上的一种更厉害 （小学语文功底） 的算法。

ps: 线段树的每种操作，不论是建树，更新树还是查询树，都是以分治为核心思想。

线段树的本质是一棵二叉树，之所以被称为线段树，是因为树里每个结点都代表一段数据，一维上来看就如同每个节点代表了一截线段 （个人见解）。

建立树：

每个节点都代表了一截线段，整颗树就代表了一整条线。将整条线分段存入一颗树中，就运用了分治的思想，以最基础的求和线段树为例（原始数组与线段树数组全部下标全部以1开始）：
定义left为当前父节点数据范围的左端点下标，right为数据右端点下标，mid=(left+right)/2。
node1代表了全部n个数据的和，以node1为父节点的node2、node3分别代表了 [ left=1,mid=(1+n)/2 ] 这段数据的和，node3 [ mid+1,right=n ] 这段数据的和；
node2代表了[1,(1+n)/2]范围内数据的和，以node2为父节点的node4、node5分别代表了 [ left=1,mid=(1+(1+n/2))/2 ] 、 [ mid+1,right=(1+n)/2 ] ，数据范围内的和；
依次类推…
直到left==right，此时树的末端有n个叶节点，分别代表了n个数据的值，"分"这个过程完成了：

if(left==right) { tree[index]=a[left];return ;}

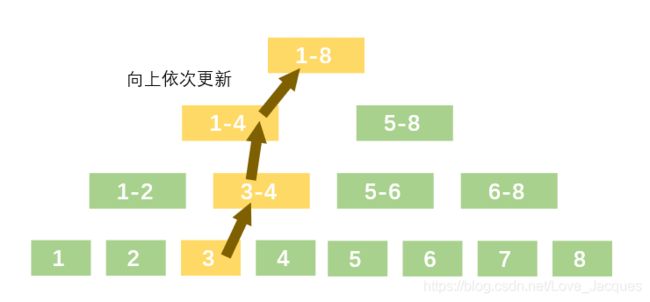
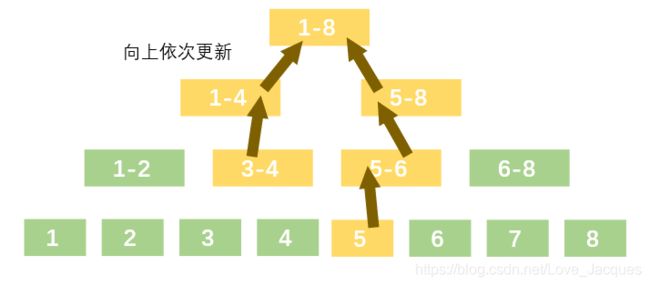
（划重点）“治” 则是从叶节点开始，往上依次更新每层父节点的值，在求和线段树中，每个父节点的值都等于左右子节点值的和：

上推数值，执行前表示当前层数值未更新，下一层数值已经更新，执行后表示当前层数值已经更新。

void push_up(int index){ tree[index]=tree[index*2]+tree[index*2+1]; }

更新树：

对于更新，笔者将其分为单节点更新与范围更新：

先说简单的单节点更新：

单节点更新我们只需要想建树一样，“分” 到线段树树的最小单元，更新此单元的值，再依次向上回溯，更新与目标节点有关的节点。

向下更新目标节点：

向上更新有关父节点：

再来谈范围更新：

范围更新与单点更新的区别就在于：“分” 的操作不一定需要达到最小单元，达到需要更新的单元即可；例如拿上图中的线段树为例，我们需要更新[3,5]这个范围内的数，则需要向下达到[3,4]和[5,5]这两个单元，更新这两个单元的值之后再向上回溯即可。

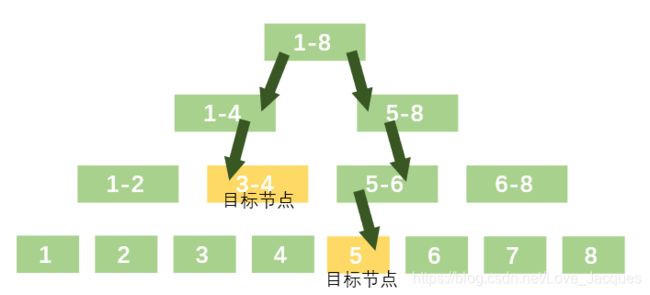
那么看到这里，想必各位大佬们也以及发现了，我们在更新[3,5]这段数据时，向下传递只传递到了[3,4]区间，而[3,3]和[4,4]的值并没有更新，这样做有没有什么特殊的用以呢？

接下来我们引入线段树的时间复杂度和空间复杂度：

线段树的复杂度：

空间复杂度：

敲一个线段树算法的代码，其空间可以认为是由线段树数组来决定的，大家可以依据上面例图来粗略估算一下线段树的空间是由层数决定的，设层数为x，则整个线段树所需的空间即为：
数学蒟蒻就不继续推导了，直接告诉大家最后的结论：

若初始数组有n个元素，则线段树数组开需要4*n的空间。

时间复杂度：

讲完了空间复杂度这个小插曲，我们接着来看为什么范围更新的时候没有下推到最底层呢？
假设我们现在要更新[1,n]这n个元素，如果下推到最底层，就相当于进行了n次单点更新，复杂度为nlogn，而如果更新次数也有多次，那么复杂度就上升到 n平方logn ，这样更新显然还不如暴力解题。
而只下推到需要的范围就来的快多了，一次范围更新最多需要logn的复杂度，多次更新最多需要nlogn的复杂度，这也是线段树真正的时间复杂的。
问题接踵而至，不下推到最底层，我要是查询最底层的数据，岂不是得不到正确的答案了？
我们接下来来看查询树部分。

查询树：

前文说到，我们进行范围更新的时候，采用只下推到需要的层数，节约了大量时间，而对于之后未更新数值的层数，我们需要在此处添加一个标记 ：表示当前层数值已经更新，下层数值还未更新。

而当我们一层一层往下查询的时候，遇到这个标记，我们将标记下推一层，继续更新之后的数值便可，假设我要查询最底层的数据，那么这个标记就会伴随我们的查询来到最底层，更新路径上的全部数值，包括最底层的数值。
再次强调，标记的含义是：表示当前层数值已经更新，下层数值还未更新。

这里给上下推标记的伪代码：

void push_down(int left,int right,int index,long long k){
	 //更新tree[index*2]的值；
	 //更新mark[index*2]的值，即为更新左子节点的标记；
	 //更新tree[index*2+1]的值；
	 //更新mark[index*2+1]的值，即为更新右子节点的标记；
	 //清空mark[index]，即清空当前层的标记；
}

至此，一颗完整的基础线段树模板已经讲完了，查询也可以分为单点查询和范围查询，原理与单点更新与范围更新大同小异，但有些题目可能会给出一些特殊的查询条件，此处就不详细展开，读者可以根据题意自写查询代码。

模板代码（以求和树为例）：

建树：

void build_tree(int left,int right,int index)
{
	 mark[index]=0;
	 if(left==right) tree[index]=a[left];
	 else{
	 	 int mid=(left+right)>>1;
	 	 build_tree(left,mid,index*2);
	 	 build_tree(mid+1,right,index*2+1);
	 	 push_up(index);
	 }
	 return ;
}

单点更新：

//单点修改不用加标记 
void signl_update(int goal,int left,int right,int index,int k)
{
	 if(left==right&&left==goal) tree[index]+=k;
	 else{
	 	 int mid=(left+right)>>1;
	 	 if(goal<=mid) signl_update(goal,left,mid,index*2,k);
	 	 else signl_update(goal,mid+1,right,index*2+1,k);
	 	 push_up(index);
	 }
	 return ;
}

范围更新：

void interval_update(int gleft,int gright,int left,int right,int index,int k)
{
	 if(left>=gleft&&right<=gright){
	 	 tree[index]+=(right-left+1)*k;
	 	 mark[index]+=k;
	 }else{
	 	 if(mark[index]!=0) push_down(left,right,index,k);
	 	 int mid=(left+right)>>1;
	 	 if(mid>=gleft) interval_update(gleft,gright,left,mid,index*2,k);
	 	 if(mid+1<=gright) interval_update(gleft,gright,mid+1,right,index*2+1,k);
	 	 push_up(index);
	 }
	 return ;
}

范围查询：

long long interval_query(int gleft,int gright,int left,int right,int index)
{
	 if(left>=gleft&&right<=gright) return tree[index];

	 if(mark[index]!=0) push_down(left,right,index,mark[index]);
	 long long mid=(left+right)>>1,answer=0;
	 if(mid>=gleft) answer+=interval_query(gleft,gright,left,mid,index*2);
	 if(mid+1<=gright) answer+=interval_query(gleft,gright,mid+1,right,index*2+1);
	 return answer;
}

专题例题：

夜深了，人静了，等咕咕咕博主明天起床更新。

更新于2020.7.20凌晨