机器学习之决策树原理及其python实现

写在前面

这是我开始入坑的第一篇博客，全部内容基于我的理解和参考博客，参考书籍为李航的《统计学习方法》。如有不对的地方欢迎评论指出，谢谢大家。

决策树

1.决策树的定义

《统计学习方法》中提出，决策树是一种基本的分类与回归方法。决策树模型呈现树状结构，在分类问题中，表示基于特征对实例进行分类的过程。决策树学习通常包括三个步骤：特征选择、决策树生成和决策树修剪。

分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点和有向边组成。结点有两种类型：内部结点和叶结点。内部结点表示一种特征和属性，叶结点表示一个类。

用决策树分类，从根结点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子结点；这事每个结点对应该特征的一个取值。如此递归地对实例进行测试并分配，直至达到叶结点。最后将实例分到叶结点地类中。

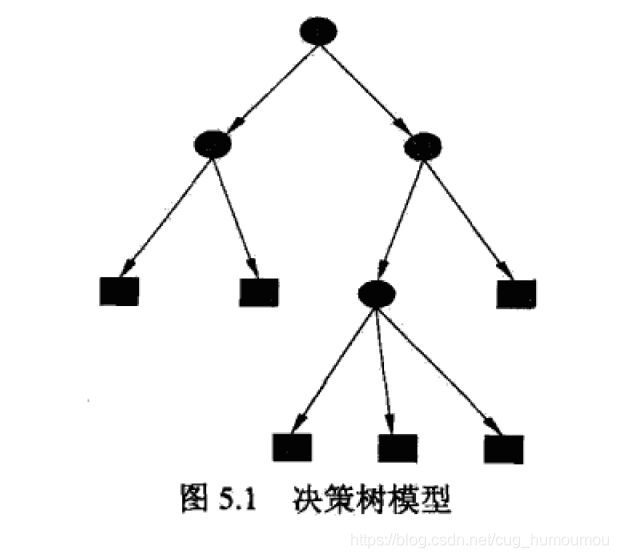
2.决策树我的理解

上面的官方定义说完了，现在用个例子来说明决策树模型。夏天到了，你突然很想吃冰西瓜。然后你来到西瓜店，但是你不知道什么样的西瓜是好西瓜，你发微信问你妈，你妈发了张图给你。

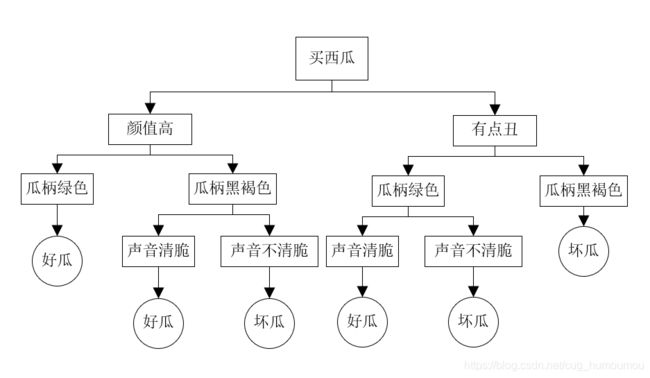
选瓜的时候，首先看颜值，圆润的一般好瓜比较多，长得丑的一般也不愿意买。光看颜值是不够的，这时候，看看瓜柄，瓜柄的好坏能看出这个瓜新不新鲜，但是也有可能放的时间稍微有点久，但是瓜，还是可以买，也是好瓜，接下来敲敲西瓜，听声音。最后你选了个好瓜，带回家了。

这里面，买西瓜的整个流程就构成了决策树模型。决策树模型的作用就是在帮你逐渐接近你想要的目标。你从一开始完全不懂的时候去选瓜，那么是好是坏全凭天意。拿到你妈发给你的表的时候，你根据颜值、瓜柄和声音，最后选出了好瓜。而颜值、瓜柄和声音就代表着西瓜的一种特征。最后好坏与否，就是决策树模型的一个类。

那么，我们为什么选出这个特征作为决策树的叶结点？比如为什么我们不把黄西瓜和绿色西瓜放一块，它们的颜色也是不同的，那么根据这两种颜色能不能判断出西瓜的好坏？答案是不能，因为绿色和黄色是西瓜的两个品种，根据这条信息，我们选择出的西瓜，并不能帮助我们减少找到好西瓜的不确定性。也就是，就算利用黄色和绿色对西瓜分了类，我们挑选出好西瓜和坏西瓜的概率，和没分类之前一样。那么这个特征除了增加了模型的复杂度，基本上没有作用。那么，在决策树模型中，特征选择的准则就是信息增益和信息增益比。

特征选择

信息增益

《统计学习方法》中对信息增益的定义为，表示特征信息X的信息而使得类Y得信息的不确定性减少。

还是用买西瓜举例子，我们在没有得到老妈的表的时候，我们完全没办法缩小我们的挑选范围。但是，得到表后，我们先根据颜值，将西瓜区分一下，这时候我们在颜值高的西瓜中，挑选一个，就有1/2的概率选中好瓜，这说明颜值这个特征帮助我们缩小了选西瓜的范围，排除了那些不好看的。也就是帮助我们减小了选瓜的不确定性。那么这个特征的信息增益符合我们的要求，就应该出现在决策树模型中。

那么，选瓜不确定性是什么？

信息熵定义了一个随机变量的不确定性，熵越大，随机变量的不确定性也就越高。

之前我们只知道，信息增益可以帮助我们进行特征选择，排除掉没用的特征。但是信息熵的出现，定义了不确定性。这时候我们就可以量化我们的信息增益。

还是用西瓜解释一下这个公式。假如现在有十个西瓜，我们在没得到表之前，获得好西瓜的经验熵（不确定性）为H(D)，之后我们得到表，根据颜值，将瓜分类了，这时候我们获得好瓜的经验熵为H(D|A)。那么特征A对于我们选西瓜这件事，有多大的作用，也就是能帮助我们将选瓜的不确定性降低多少，通过H(D)和H(D|A)的差值，也就定量的表达出特征A的作用。也就是信息增益。

那么经验熵怎么计算呢？书中给出计算步骤如下：



这部分没啥好说的，就是套公式计算就行。

信息增益比

既然信息增益可以帮助我们进行特征选择，为什么还需要特征增益比呢？这里面涉及一个问题。还是以西瓜为例，现在你一周，每天买西瓜，记录如下：

周一	周二	周三	周四	周五	周六	周日
小明	小红	小明	小明	小红	小红	小红
好	不好	好	不好	好	好	不好

那么我们现在假如用周几作为特征A，因为每一天都将样本完全分开，求得的H(D|A) = 0。然后我们使用店家作为特征B，求得H(D|Ｂ) = 0.679。这时候，哇塞，肯定是用周几作为特征好啊，信息增益这么大。但是应该都清楚，这种特征对于样本的分割没有任何的意义。这是因为，在相同条件下，信息增益会偏向分类较多的特征。为了解决这个问题，这时候就需要信息增益比出场了。

算法实现

ID3算法

代码部分：
下面展示一些 内联代码片。

import numpy as np


# 载入训练数据
def LoadData(filename):
    data = []
    label = []
    file = open(filename)

    for line in file.readlines():
        curline = line.strip().split(',')
        data.append([int(int(dt) > 128) for dt in curline[1:]])   #二值化
        label.append(int(curline[0]))
    return data, label


# 计算经验熵H(D)
def cal_H_D(trainLabel):
    H_D = 0
    arr = [0] * 10
    for i in trainLabel:
        arr[int(i)] += 1
    for j in arr:
        if j != 0:
            p = j / len(trainLabel)
            H_D += -1 * p * np.log2(p)
    return H_D


# 计算条件熵H(D|A)
def cal_H_D_A(feature, trainLabel):
    label0 = []
    label1 = []

    # 已经二值化，所以可能取值为0和1
    for i in range(feature.size):
        if feature[i] == 0:
            label0.append(trainLabel[i])
        else:
            label1.append(trainLabel[i])
    H_D_A = (len(label0) / len(feature) * cal_H_D(label0)) + (len(label1) / len(feature) * cal_H_D(label1))
    return H_D_A


# 我这里用的是Mnist数据集，所以标签只有0-9
def MaxClass(trainLabel):
    label = [0] * 10
    for i in trainLabel:
        label[int(i)] += 1
    return label.index(max(label))

# 挑选出信息增益最大的特征
def getFeature(trainData, trainLabel):
    trainData = np.array(trainData)
    trainLabel = np.array(trainLabel)
    featureNum = trainData.shape[1]
    MaxG_D_A = -1
    feature = -1
    for i in range(featureNum):
        H_D = cal_H_D(trainLabel)
        G_D_A = H_D - cal_H_D_A(trainData[:, i], trainLabel)
        if G_D_A > MaxG_D_A:                    
            MaxG_D_A = G_D_A
            feature = i
    return MaxG_D_A, feature


# 根据书中的ID3算法步骤的第五步，对数据集进行拆分
def splitData(trainData, trainLabel, Ag, value):
    ReTrainData = []
    ReTrainLabel = []
    for i in range(len(trainData)):
        if trainData[i][Ag] == value:
            ReTrainData.append(trainData[i][0:Ag] + trainData[i][Ag+1:])
            ReTrainLabel.append(trainLabel[i])
    return ReTrainData, ReTrainLabel


# 根据书上的算法流程，利用递归建立决策树
def creatFeatureTree(trainData, trainLabel):
    
    feature = {label for label in trainLabel}
    Threshold = 0.1 #阈值

    print(len(trainData[0]), len(trainLabel))

    if len(feature) == 1:
        return trainLabel[0]
    if len(trainData[0]) == 0:
        return MaxClass(trainLabel)
    
    gain, Ag = getFeature(trainData, trainLabel)
    if gain < Threshold:
        return MaxClass(trainLabel)
    
    Tree = {Ag:{}}
    
    trainData0, trainLabel0 = splitData(trainData, trainLabel, Ag, 0)
    Tree[Ag][0] = creatFeatureTree(trainData0, trainLabel0)
    trainData1, trainLabel1 = splitData(trainData, trainLabel, Ag, 1)
    Tree[Ag][1] = creatFeatureTree(trainData1, trainLabel1)
    return Tree


def predict(testDataList, tree):
    while True:
        (key, value), = tree.items()
        if type(tree[key]).__name__ == 'dict':
            dataVal = testDataList[key]
            del testDataList[key]

            tree = value[dataVal]

            if type(tree).__name__ == 'int':
                return tree

        else:
            return value


def test(testDataList, testLabelList, tree):
    errorcnt = 0
    for i in range(len(testDataList)):
        if testLabelList[i] != predict(testDataList[i], tree):
            errorcnt += 1
    return 1 - errorcnt / len(testDataList)


if __name__ == "__main__":
    
    print('read train data')
    trainData, trainlabel = LoadData('Mnist/mnist_train/mnist_train.csv')

    print('read test data')
    testData, testlabel= LoadData('Mnist/mnist_test/mnist_test.csv')

    print('start creat tree')
    Tree = creatFeatureTree(trainData, trainlabel)
    print(Tree)

    print('start test')
    accur = test(testData, testlabel, Tree)
    print('accurancy is: ', accur)

C4.5算法

C4.5算法与ID3算法相似，主要是特征选择部分，采用了信息增益比来进行特征选择。

代码实现部分，参考上面，就不写了。

CART决策树

CART决策树的生成采用了基尼指数选择最优特征，同时决定了 该特征的最优二值切分点。

CART树的生成：


代码实现：

import numpy as np
import math


T = 0

# 载入数据
def LoadData(filename):
    data = []
    label = []
    file = open(filename)

    for line in file.readlines():
        curline = line.strip().split(',')
        data.append([int(int(dt) > 128) for dt in curline[1:]])   #二值化
        label.append(int(curline[0]))
    return data, label

# 返回分类标签
def MaxClass(trainLabel):
    label = [0] * 10
    for i in trainLabel:
        label[int(i)] += 1
    return label.index(max(label))

# 计算基尼指数
def Gini(trainlabel):
    p = 0
    label = [0] * 10
    for i in trainlabel:
        label[int(i)] += 1
    for j in label:
        p += math.pow((j / len(trainlabel)), 2)
    return 1 - p


def calcGini(feature, trainlabel):
    GiniValue = -1
    label0 = []
    label1 = []

    for i in range(feature.size):
        if feature[i] == 0:
            label0.append(trainlabel[i])
        else:
            label1.append(trainlabel[i])
    if len(label0) == 0:
        GiniValue = Gini(label1)
    elif len(label1) == 0:
        GiniValue = Gini(label0)
    else:
        GiniValue = len(label0) / trainlabel.size * Gini(label0) + len(label1) / trainlabel.size * Gini(label1)
    return GiniValue

# 获得最优特征
def getFeature(trainData, trainLabel):
    trainData = np.array(trainData)
    trainLabel = np.array(trainLabel)
    featureNum = trainData.shape[1]
    MinGini = 100
    feature = -1
    for i in range(featureNum):
        Gini = calcGini(trainData[:, i], trainLabel)
        if Gini < MinGini:
            MinGini = Gini
            feature = i
    return MinGini, feature

# 拆分数据
def splitData(trainData, trainLabel, Ag, value):
    ReTrainData = []
    ReTrainLabel = []
    for i in range(len(trainData)):
        if trainData[i][Ag] == value:
            ReTrainData.append(trainData[i][0:Ag] + trainData[i][Ag+1:])
            ReTrainLabel.append(trainLabel[i])
    return ReTrainData, ReTrainLabel

# 创建CART决策树
def creatCARTtree(trainData, trainLabel):
    global T
    feature = {label for label in trainLabel}
    Threshold = 0.2

    print(len(trainData[0]), len(trainLabel))
    if len(feature) == 1:
        T += 1
        return trainLabel[0], 0
    if len(trainData[0]) == 0:
        T += 1
        return MaxClass(trainLabel), 0
    
    Gini, Ag = getFeature(trainData, trainLabel)
    if Gini < Threshold:
        T += 1
        return MaxClass(trainLabel), Gini
    
    Tree = {Ag:{}}
    Gini_tree = {Gini:{}}
    trainData0, trainLabel0 = splitData(trainData, trainLabel, Ag, 0)
    Tree[Ag][0], Gini_tree[Gini][0] = creatCARTtree(trainData0, trainLabel0)
    trainData1, trainLabel1 = splitData(trainData, trainLabel, Ag, 1)
    Tree[Ag][1], Gini_tree[Gini][1] = creatCARTtree(trainData1, trainLabel1)
    return Tree, Gini_tree

# 预测数据
def predict(testDataList, tree):
    while True:
        (key, value), = tree.items()
        if type(tree[key]).__name__ == 'dict':
            dataVal = testDataList[key]
            del testDataList[key]

            tree = value[dataVal]

            if type(tree).__name__ == 'int':
                return tree

        else:
            return value

# 计算准确率
def test(testDataList, testLabelList, tree):
    errorcnt = 0
    for i in range(len(testDataList)):
        if testLabelList[i] != predict(testDataList[i], tree):
            errorcnt += 1
    return 1 - errorcnt / len(testDataList)


if __name__ == "__main__":
    
    print('read train data')
    trainData, trainlabel = LoadData('Mnist/mnist_train/mnist_train.csv')

    print('read test data')
    testData, testlabel= LoadData('Mnist/mnist_test/mnist_test.csv')
    
    print('start creat tree')
    Tree, Gini_tree = creatCARTtree(trainData, trainlabel)
    print(Tree)

    print('start test')
    accur = test(testData, testlabel, Tree)
    print('accurancy is: ', accur)

三种算法的对比

ID3 算法的不足：
（1）在相同条件下，信息增益的特征选择偏向于比较多的特征
（2）没有考虑过拟合问题

C4.5 算法改进：
（1）采用信息增益比代替信息增益

CART 树改进：
（1）使用基尼指数进行特征选择
（2）采用后剪枝法，即先生成决策树，再产生所有可能的剪枝后的CART树，然后采用交叉验证，选择泛化能力最好的决策树。

参考博客: 决策树原理剖析及实现.