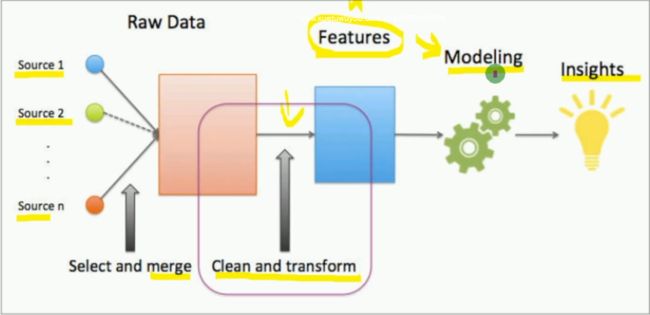
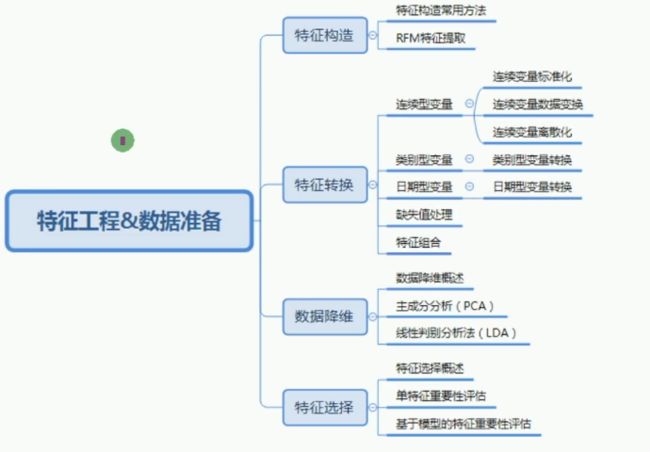
对于数据挖掘,数据准备阶段主要就是进行特征工程。
数据和特征决定了模型预测的上限,而算法只是逼近了这个上限。
好的特征要少而精,这会使模型更简单、更精准。
一、特征构造
1.’常见提取方式
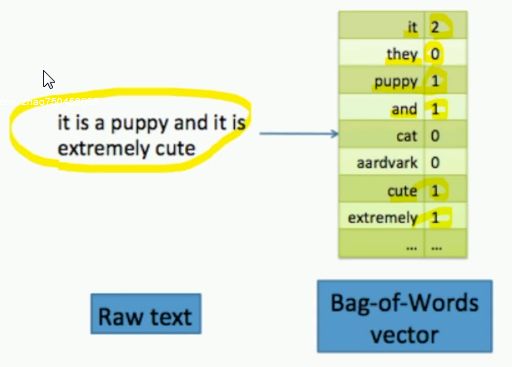
文本数据的特征提取
词袋向量的方式:统计频率
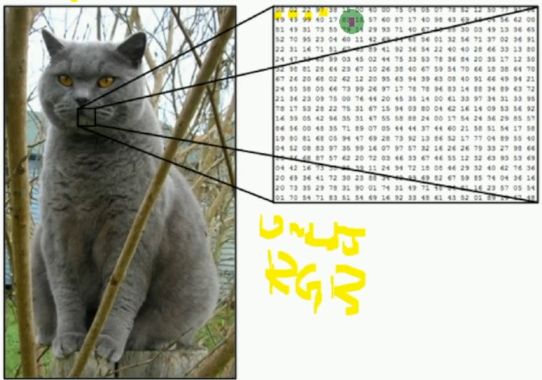
图像数据的特征提取
像素点RGB
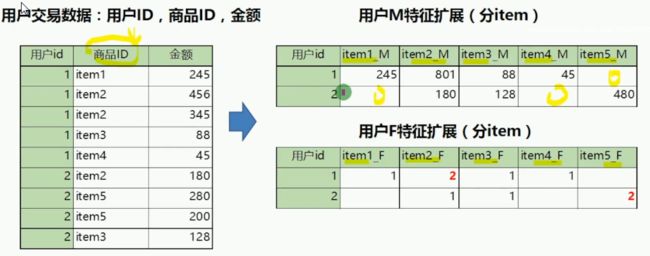
用户行为特征提取
特征提取总结:
- 特征设计时需要与目标高度相关:
这个特征对预测目标是否有用
如果有用,这个特征的重要程度如何
这个特征的信息是否在其他特征重体现过
- 特征需要专业领域知识、直觉和一定的数学知识
- 初始提取的特征后续还要进行特征转换处理,再进入算法模型
- 特征设计和提取需要不断反复迭代验证,是一个非常耗时的工作
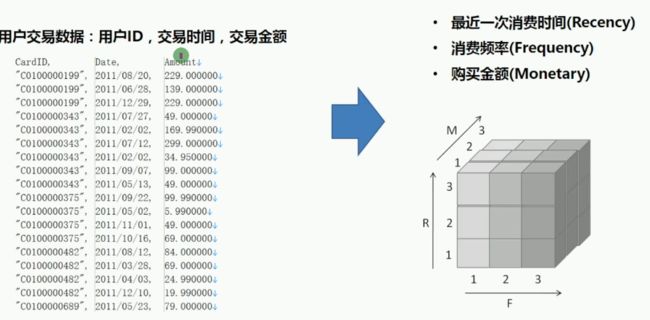
2.RFM
在客户关系(CRM)领域,三个刻画用户的神奇指标:
- 最近一次消费间隔时长(Recency)
- 消费频率(Frequency)
- 消费金额(Monetary)
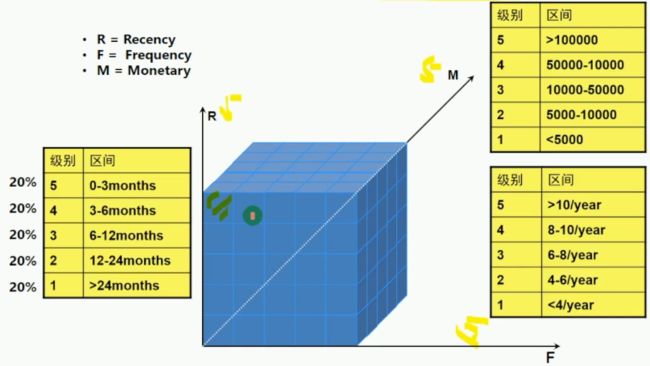
RFM分析方法有一种叫五等分法
把RFM切成5个人数等分区间,然后形成RFM的组合立方体
125个格子
R越小越好,FM越大越好
R是越小,等级越大,于是RMF统一为等级越大越好
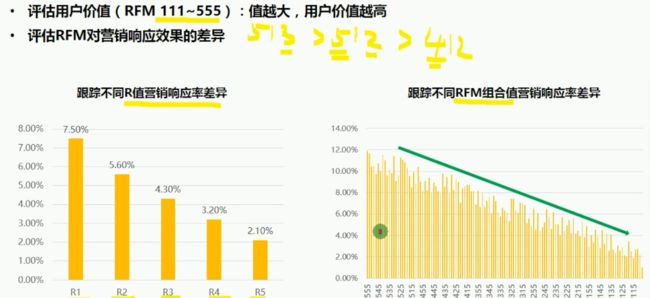
因此用户的等级范围是111-555
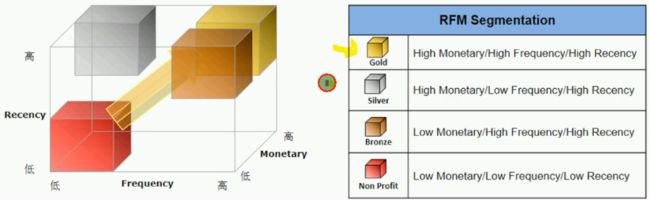
RFM应用价值:用户细分
111-555共125个群体,比较多,可以做一些合并
根据不同的RFM值组合情况,可以把用户分成不同群体,以便制定差异化策略
RFM应用价值:用户价值及营销响应评估
二、特征转换
1.连续变量无量纲化处理
使不同规格尺度的数据转换到同一规格尺度
目的:
- 无量纲化可以让不属于同一量纲的特征值可以比较:例如身高(cm),体重(kg)
- 无量纲化后模型收敛会加快(运行速度较快)
- 无量纲化对一些模型的结果影响比较大,例如聚类模型,无量纲化后效果会更好 基于距离的一些模型
常用无量纲化方法--标准化
效果:把原始的连续变量转换为均值为0,标准差为1的变量
${x}'=\frac{x-\bar{x}}{\delta }$
常用无量纲化方法--区间缩放法
效果:把原始的连续变量转换为范围在a-b之间的变量,常见的a=0,b=1
${x}'=\frac{x-\min(x)}{\max(x)-\min(x) }$
2.连续变量数据变换
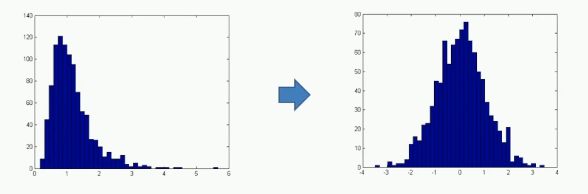
数据变换:通过函数变换改变原数据的分布
目的:
- 变换后更便捷地发现数据之间的关系:从没有关系变成有关系
- 很多数据呈现严重的偏态分布(很多偏小的值聚集在一起),变换后差异可以拉开
- 让数据更符合模型理论所需要的假设,然后对其分析,例如变换后数据呈现正态分布
常用的数据变换方法
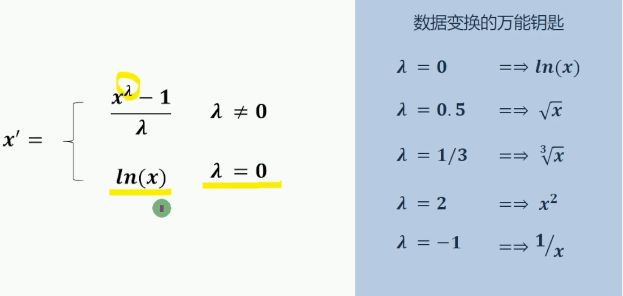
- log变换 x=ln(x)
- box-cox变换,自动寻找最佳正态分布变换函数的方法
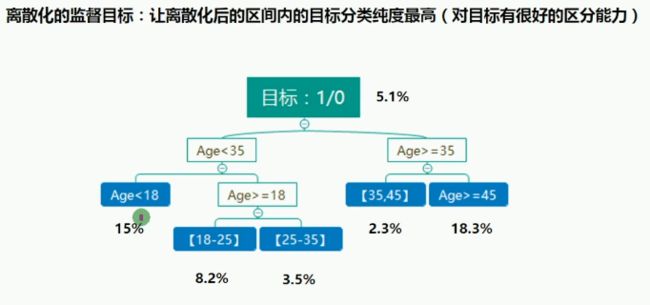
3.连续变量离散化
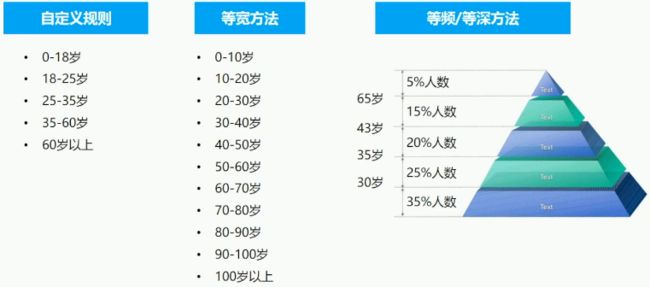
把连续型的数值切割为少数的一些区间,例如年龄值切割为5个年龄段
目的:
- 方便探索数据分布和相关性,例如直方图,交叉表
- 离散化后的特征对异常数据有很强的鲁棒性:减少异常数据对模型的影响
- 离散化后可以进行特征交叉组合,由M+N个特征变量变为M*N个特征变量
- 特征离散化后,模型会更稳定
- 特征离散化后,简化了模型复杂度,降低了过拟合风险
- 一些模型(关联模型)要求输入特征是离散的
离散化方法:
非监督离散化方法
有监督的离散化:决策树
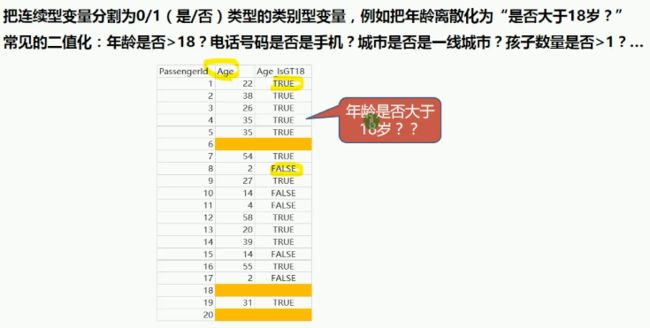
一种特殊的离散化:二值化
一种特殊的离散化:Rounding(取整)
4.类别变量编码
把类别型变量编码成数值型的变量
目的:
- 很多机器学习算法无法处理类别型变量,必须转换为数值型变量
- 一定程度上起到了扩充特征的作用(构造了新的特征)
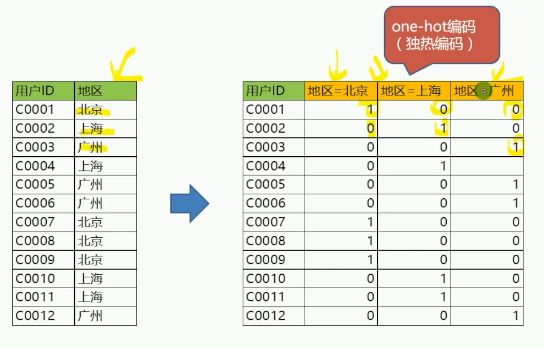
one-hot编码
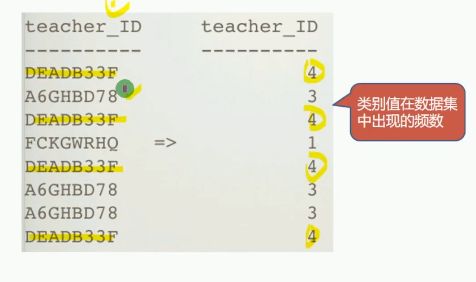
Counting Encoding
用类别的频数来编码,也可以对频数去量纲化(秩序,归一化等)
Target Encoding
用目标变量(二分类)中的某一类的比例来编码
5.日期型变量处理
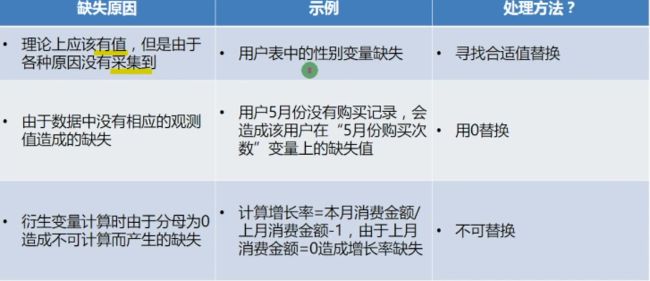
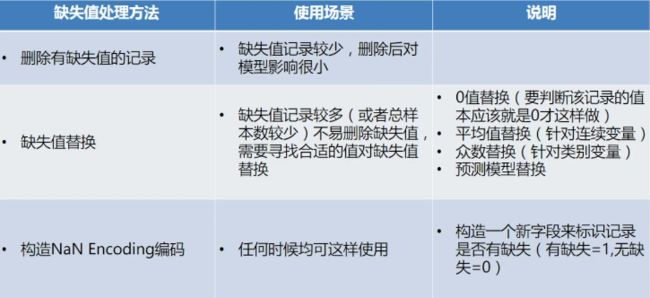
6.缺失值处理
缺失值原因
处理方法
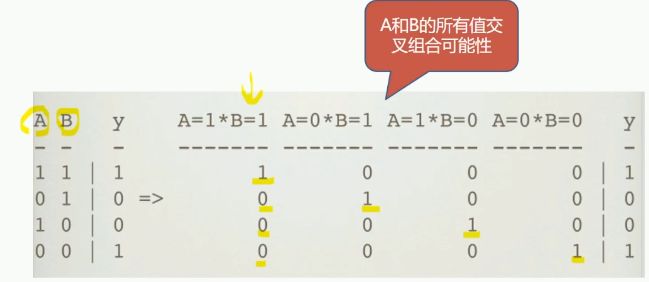
7.特征组合
目的:通过特征组合构造出更多/更好的特征,提示模型精度
组合让特征更加精细,反映了原始多个特征之间的交互关系。
特征组合的方法
示例
三、数据降维
在尽量少减少信息量的前提下,采用某种映射方法(函数),把原来的高维(变量多)数据映射为低维数据(变量少)
降维原因:
- 维数灾难:高维情况下容易发生模型的过拟合(泛化能力弱)
- 特征之间有明显的自相关的时候,也要考虑降维,因为自相关会让模型效果变差
- 降维可以对数据中的有效信息进行综合提取,并去除一些无用的噪音信息
- 降维后降低模型复杂度,减少模型训练时间
- 降维之后可以对数据进行可视化分析
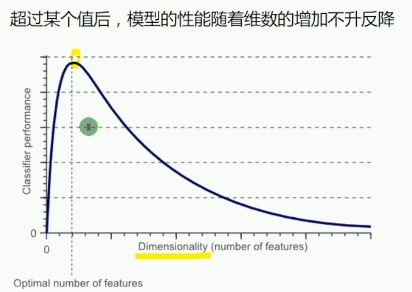
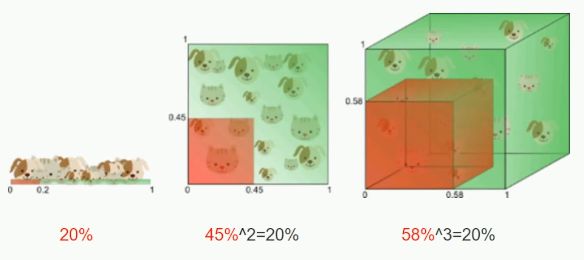
维数灾难
维数灾难原因
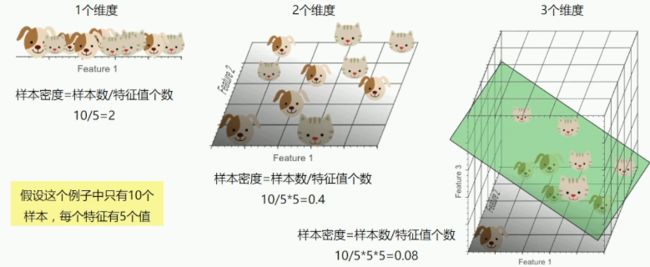
当特征值(空间)个数趋向无限大时,样本密度非常稀疏,训练样本被分错的可能性趋向于零
降维后发生什么?
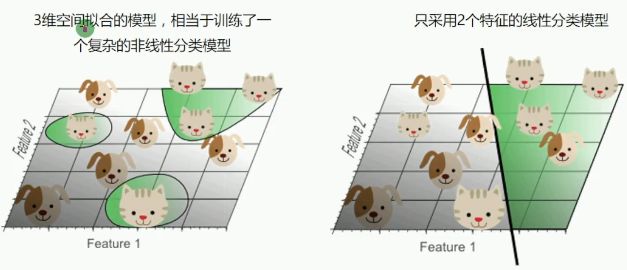
线性模型可能精确度会下降,但是也会避免出现过拟合现象
避免维度灾难的一个方法是增加样本量
样本密度:样本数/特征值个数;当增加维度时,保持样本密度不变的方法就是增加样本量
常用降维方法
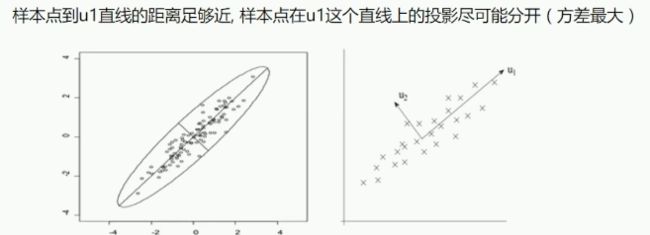
主成分分析
通过某种线性投影,将高维数据映射到低维空间中表示,并期望在所投影的维度上数据方差最大。使用较少的数据维度,尽量保留住较多的数据信息。
PCA操作流程
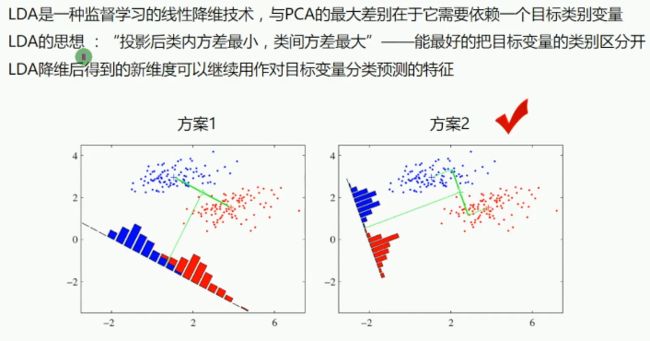
线性判别分析法
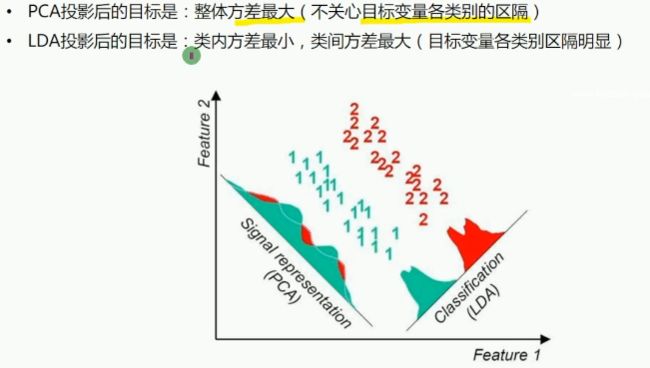
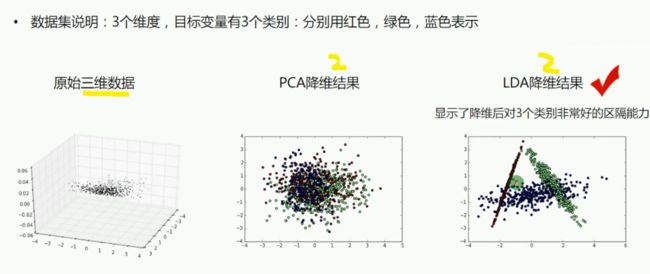
PCA与LDA
实验结果
总结:
- 如果研究的问题有目标变量(类别型)
优先使用LDA来降维
可以使用PCA做小幅度的降维去噪声,然后再使用LDA降维
- 如果研究的问题没有目标变量
优先使用PCA来降维
四、特征选择
特征选择与降维
特征选择原因:
- 提高预测准确性
- 构造更快,消耗更低的预测模型
- 能够对模型有更好的理解和解释
特征选择的方法
单特征重要性评估
过滤方法
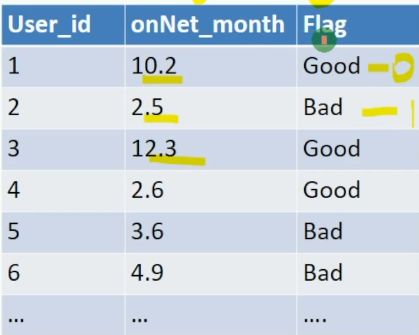
苹果onNet_month与Flag(目标)指标的相关性
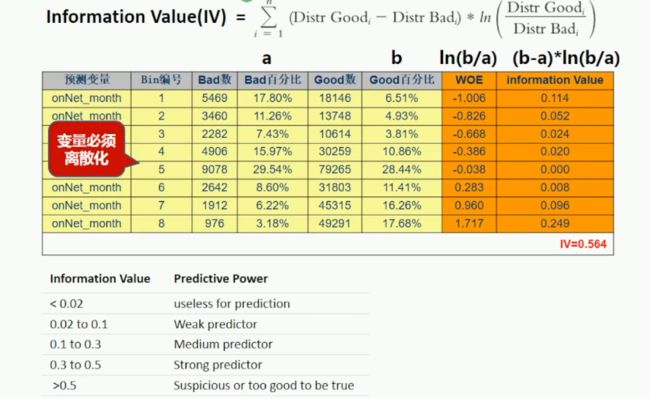
信息值(IV)
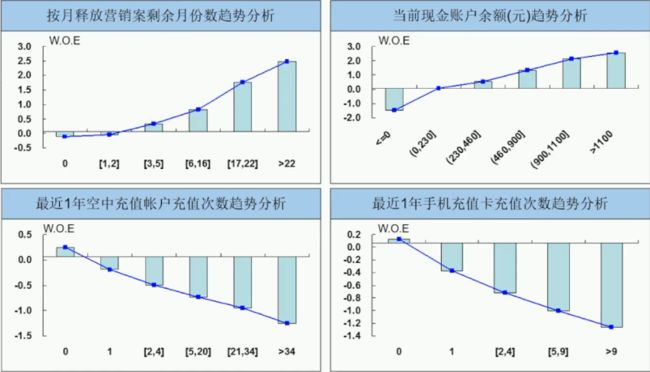
变量重要性可视化:趋势分析
更多指标