Android电子书翻页效果

效果如图:

思路：计算出出各个顶点作为path路径连接 如图

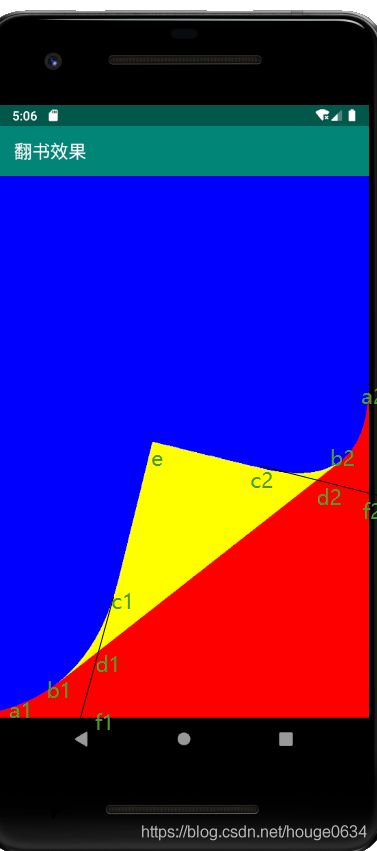
设屏幕右下角为原点O (view宽,view高),e为手指触摸屏幕的坐标，我们先算出点f1与f2的坐标

此处em代表两个点的线段距离,下文同上!
em=O.y-e.y(屏幕高度-e的Y坐标) ,Om=O.x-e.x; （.x代表某个点的x坐标）
可知方程 ef1²-f1m²=em²(勾股定理) ef1-f1m=Om; 因为em=Of1
=>(ef1+f1m)(ef1-f1m)=em²
=>(2ef1-Om）* Om=em²
=>ef1=(em²/Om+Om)/2;
=>f1.x=O.x-ef1

//pointF e 求f1坐标
float Om=getMeasuredWidth()-em.x;
float em=getMeasuredHeight()-em.y;
float ef1=(em*em/Om+Om)/2;
f1.x=getMeasuredWidth()-ef1;
f1.y=getMeasuredHeight();

根据方程可计算出 f1坐标 ,同理计算出f2坐标 。 注: (应该有更简单的计算公式,不过我高中和大学数学都忘了个差不多了。。。总之先计算f1,f2坐标)；

=======================================================
接下来计算a1和a2
我们这里让a1.x=f1.x-(O.x-f1.x)/2
float a1x=f1.x-(O.x-f1.x)/2;
PointF a1=new PointF(a1x,view高)
同理得a2

===========================================
接下来计算c1 和 c2
c1 实际上是 直线a1–a2 与 直线e–f1的交点:
通过直线函数求两条线的交点 如下:

 public PointF getIntersection(PointF pointF1,PointF pointF2, PointF pointF3,PointF pointF4){
        //第一条直线
        float x1 = pointF1.x, y1 = pointF1.y, x2 = pointF2.x, y2 =     				pointF2.y;
        float a = (y1 - y2) / (x1 - x2);
        float b = (x1 * y2 - x2 * y1) / (x1 - x2);
       

        //第二条直线
        float x3 = pointF3.x, y3 = pointF3.y, x4 = pointF4.x, y4 = pointF4.y;
        float c = (y3 - y4) / (x3 - x4);
        float d = (x3 * y4 - x4 * y3) / (x3 - x4);
 

        float x = ((x1 - x2) * (x3 * y4 - x4 * y3) - (x3 - x4) * (x1 * y2 - x2 * y1))
                / ((x3 - x4) * (y1 - y2) - (x1 - x2) * (y3 - y4));

        double y = ((y1 - y2) * (x3 * y4 - x4 * y3) - (x1 * y2 - x2 * y1) * (y3 - y4))
                / ((y1 - y2) * (x3 - x4) - (x1 - x2) * (y3 - y4));

        PointF pointF = new PointF((int)x, (int)y);
        return pointF;
    }

接下来求b1和b2
b1 在 三角形a1–c1–f1 中
zxp1.x=((zp1.x+jiao1.x)/2+p2.x)/2;

PointF b1=new PointF();
b1.x=((a1.x+c1.x)/2+f1.x)/2;
b1.y=((a1.y+c1.y)/2+f1.y)/2;
//同理的b2

用Path对象将已求得点连接效果如下:

填充效果:

看起来别扭是因为在连接 c1–b1 以及 b1–a1时 用lineTo画直线函数连接,这里需要用贝塞尔曲线 path.quadTo();
而path.quadTo();函数需要确定偏移的点
接下来计算偏移点d1 d2 g1 g2

d1和d2很好求，就是直线ef1、ef2 与 直线b1b2的交点，通过上面的函数可得

d1=getIntersection(b1,b2,e,f1);
d2=getIntersection(b1,b2,e,f2);

g1的y坐标为view高度,而且在直线 b1–b2上

//直线函数为 Y=kx+b;计算k ,b
   public void getlineFun(PointF pointF1,PointF pointF2){//直线函数 确定一条直线函数
        //y=kx+b; x=(y-b)/k
        float x1=pointF1.x,y1=pointF1.y,x2=pointF2.x,y2=pointF2.y;
        float k=(y2-y1)/(x2-x1); //k
        float b=y1-(y2-y1)/(x2-x1)*x1;//b

        g1.y=getMeasuredHeight();
        g1.x=(g1.y-b)/k;
        g2.x=getMeasuredWidth();
        g2.y=k*g2.x+b;
    }

//得出g1,g2
getlineFun(b1,b2)

最终，在连接c1–b1向b1偏移 ，b1–a1 向g1偏移
黄色区域最终代码:

path.moveTo(e.x,e.y);
path.lineTo(c1.x,c1.y);

path.quadTo(d1.x,d1.y,b1.x,b1.y);//向点d1处偏移
path.quadTo(g1.x,g1.y,a1.x,a1.y);//向点g1偏移
path.quadTo(g1.x,g1.y,b1.x,b1.y);//回到b1点

path.lineTo(b2.x,b2.y);
path.quadTo(g2.x,g2.y,a1.x,a1.y);
path.quadTo(g2.x,g2.y,b2.x,b2.y);
path.quadTo(d2.x,d2.y,c2.x,c2.y);
path.quadTo(e.x,e.y);//回到原点

最后用 用path连接蓝色区域 用 canvas.clipPath(path);剪裁掉画布即可完成!

=======================================================
结语：本人第一次写博客，如有