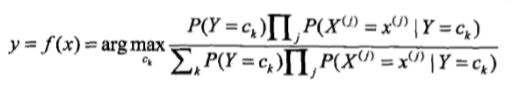朴素贝叶斯的面试看这一篇就够了
文章目录
- 0.前言
- 1.模型
- 1.1模型算法总结(精华)
- 1.2后验概率最大化
- 2.参数估计
- 3.极大似然估计
- 2.2学习分类算法
- 3.灵魂拷问
- 4.代码
- 4.1朴素贝叶斯垃圾邮件分类
0.前言
朴素贝叶斯法属于生成模型。(学习生成数据的机制)
先验概率
![]()
条件概率
![]()
后验概率
结果推原因。已知x发生的概率下,是类ck的概率。
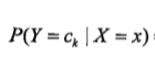
贝叶斯定理

特征条件独立假设
用于分类的特征在类确定的条件下都是条件独立的。
全概率公式
原因推结果。
条件概率公式
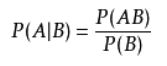
期望风险、经验风险、结构风险
参考阅读:期望风险、经验风险、结构风险
1.模型
1.1模型算法总结(精华)
- 通过训练数据集学习联合概率分布P(X,Y)。具体学习先验概率分布和条件概率分布,然后利用条件概率公式学习联合概率分布。

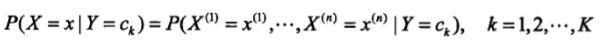
- 由于条件概率分布的参数数量是指数级的,所以朴素贝叶斯法对其作了条件独立性假设,有时会牺牲分类准确率。
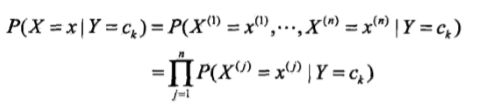
- 对于给定的输入x,通过前两步学习到的模型计算后验概率分布,输出后验概率最大的类。
上图就是贝叶斯分类器。条件概率,先验概率,都已习得,故可以求解。
公式中的分母对每一类别ck都是一样的,故可省略,最终得到:
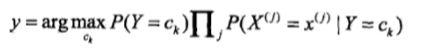
1.2后验概率最大化
这部分可以联想上一个KNN算法选取k个邻居中数目最多的类别标签。
这里将实例分类为后验概率最大的类中,实际等价与期望风险最小化。
假定选择0-1损失函数(不重要)。
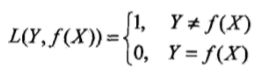
其中,f(X)为我们习得的分类决策函数。
经过一系列变换得到:

由此可印证期望风险最小化准则等价于后验概率最大化原则。
![]()
等于

2.参数估计
3.极大似然估计
先验概率P(Y=ck)的极大似然估计:

条件概率P(X(j)=aji|Y=ck)的极大似然估计:

其中xi(j)是第i个样本的第j个特征;ajl是第j个特征可能取得第l个值;I为指示函数。
2.2学习分类算法
3.灵魂拷问
4.代码
github代码地址
4.1朴素贝叶斯垃圾邮件分类
第一,介绍下步骤:
- 收集数据:分词
- 准备数据:创建词表和word2vec辅助函数
- 分析数据:确保每条邮件解析的正确性
- 训练算法:使用train方法计算先验概率和条件概率
- 测试算法:使用classifyNB方法,构建测试函数来计算错分率
- 使用算法:构建完整程序对一组文档进行分类,并将错分的文档输出
第二,记录下实战中遇到的坑。
坑一:对理论转化成实际代码的过程不熟悉。
学习了这么久理论,但是还没有实战过,因此这一次实战就让我深刻认识到了对于一个机器学习算法,看会->默写->实现,是三种不同的境界,而自己还在第一重境界中徘徊,因此总结ML算法实现流程的任务提上了日程,还好有《机器学习实战》这本书。
坑二:自己实现不出来最大的问题是输入输出不明确,数据不熟悉,通用流程不熟悉,算法思想转化代码过程不熟悉……等导致的,这个算法比较简单,没有什么代码上需要解释的。当下阶段要做的就是大量的模仿。
参考阅读:Sckit-learn上的朴素贝叶斯