哈夫曼编码
哈夫曼树的应用很广,哈夫曼编码就是其在电讯通信中的应用之一。广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%~90%之间。在电讯通信业务中,通常用二进制编码来表示字母或其他字符,并用这样的编码来表示字符序列。
例:如果需传送的电文为 ‘ABACCDA’,它只用到四种字符,用两位二进制编码便可分辨。假设 A, B, C, D 的编码分别为 00, 01,10, 11,则上述电文便为 ‘00010010101100’(共 14 位),译码员按两位进行分组译码,便可恢复原来的电文。
能否使编码总长度更短呢?
实际应用中各字符的出现频度不相同,用短(长)编码表示频率大(小)的字符,使得编码序列的总长度最小,使所需总空间量最少
数据的最小冗余编码问题
在上例中,若假设 A, B, C, D 的编码分别为 0,00,1,01,则电文 ‘ABACCDA’ 便为 ‘000011010’(共 9 位),但此编码存在多义性:可译为: ‘BBCCDA’、‘ABACCDA’、‘AAAACCACA’ 等。
译码的惟一性问题
要求任一字符的编码都不能是另一字符编码的前缀,这种编码称为前缀编码(其实是非前缀码)。 在编码过程要考虑两个问题,数据的最小冗余编码问题,译码的惟一性问题,利用最优二叉树可以很好地解决上述两个问题
用二叉树设计二进制前缀编码
以电文中的字符作为叶子结点构造二叉树。然后将二叉树中结点引向其左孩子的分支标 ‘0’,引向其右孩子的分支标 ‘1’; 每个字符的编码即为从根到每个叶子的路径上得到的 0, 1 序列。如此得到的即为二进制前缀编码。
任意一个叶子结点都不可能在其它叶子结点的路径中。
用哈夫曼树设计总长最短的二进制前缀编码
假设各个字符在电文中出现的次数(或频率)为 wi ,其编码长度为 li,电文中只有 n 种字符,则电文编码总长为:
设计电文总长最短的编码,设计哈夫曼树(以 n 种字符出现的频率作权),
由哈夫曼树得到的二进制前缀编码称为哈夫曼编码
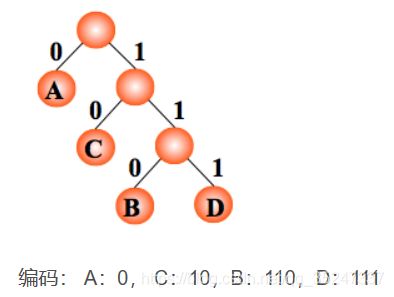
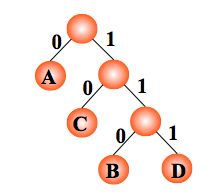
例:如果需传送的电文为 ‘ABACCDA’,即:A, B, C, D
的频率(即权值)分别为 0.43, 0.14, 0.29, 0.14,试构造哈夫曼编码。
编码: A:0, C:10, B:110, D:111 。电文 ‘ABACCDA’ 便为 ‘0110010101110’(共 13 位)。
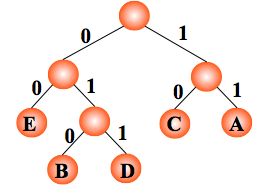
例:如果需传送的电文为 ‘ABCACCDAEAE’,即:A, B, C, D, E 的频率(即权值)分别为0.36, 0.1, 0.27, 0.1, 0.18,试构造哈夫曼编码。
编码: A:11,C:10,E:00,B:010,D:011 ,则电文 ‘ABCACCDAEAE’ 便为 ‘110101011101001111001100’(共 24 位,比 33 位短)。
译码
从哈夫曼树根开始,对待译码电文逐位取码。若编码是“0”,则向左走;若编码是“1”,则向右走,一旦到达叶子结点,则译出一个字符;再重新从根出发,直到电文结束。
电文为 “1101000” ,译文只能是“CAT”
----------------------------------------------
转载:https://www.cnblogs.com/wkfvawl/p/9783271.html