机器学习——回归实践（预测某一时间点在下一时刻的PM2.5）

前言

在看完《机器学习实战》这本书的第八章之后，相对之前入门的时候，学习的李宏毅老师的机器学习的回归部分进行总结（那已经是去年的事了…）。
当时作业一是预测某一时间点在下一时刻的PM2.5，我怎么着都对代码不熟悉，以至于我去学习了一遍Python基础，回过头还是挺懵，我估计是我不适合从李宏毅老师的视频入门，所以我推荐基础不大好的同类们从《机器学习实战》这本书入门机器学习，里面不会有太多数学推导过程，非常实用，我认为学习机器学习得先理解其运行流程与使用，至于数学推导等细节方面，还是等做项目需要的时候再回头学习，这样对算法会有更深刻的印象与理解。

注：本文是以三个步骤对本次实例进行分析，整体可运行代码会在最后一个部分给出，中间部分代码可能不能单独运行，还望的耐心看下去。(*^▽^*)

1.数据集分离

我们的目的是要预测某一时间点在下一时刻的PM2.5

• 测试资料里，每个时间点以一个ID表示，共240笔测试资料，也就是240个时间点。
• 评比标准：预测值和实际值的平方误差平均值。
• 预测根据：前九个小时的所有观测数据。
• 数据集下载：由于github在我这边又进不去了，所以只能通过CSDN下载，网址如下：https://download.csdn.net/download/qq_42263553/12574125
  里面包含了李宏毅老师机器学习这门课的所有代码，如果没有C币请在评论区留下你的163邮箱我私发给你。

读取与解析训练集

首先我们第一步就是要解析数据，之前我所学的是对txt文件的数据集进行解析，在这里，训练集数据量庞大，采用.csv文件进行存储。我们第一步就是要将训练集与对应的预测值用数组进行保存并返回。
代码如下所示：

"""
函数说明：读取训练数据，用传入的列表进行保存
参数：
data - 用以保存整个训练集的数据的空列表，这个列表内部又包含18个列表，代表18项污染物指标
返回值：
data - 读取完训练集数据返回的列表，这个内部有18个列表，也就是十八行
每一行代表一个污染指标，每一行存储的是训练集中属于这个污染指标的所有的数据
"""
def Read_TrainData(data):
    #read data
    #读取训练数据，把训练数据都取出来用一个data列表，训练数据是每个月前20天每个小时的气象资料（每小时有18种测资）
    #列表中有18个小列表，小列表就是一个小项。代表有十八行
    #每个小列表里面有24*240=5760个数据，因为每18个项目后，下一个24列又从data[0]开始存
    n_row = 0
    text = open('data/train.csv', 'r', encoding='big5')
    row = csv.reader(text, delimiter=',')#使用csv读取表格
    for r in row: #row是一个迭代器，每次迭代一行
        if n_row != 0: #过滤第一行，因为都是名称，从第二行一直到最后一行
            for i in range(3,27):#从第二行的三列数据逐行读取，抛弃前面的无用项目
                if r[i] != "NR":#第二行的第三个数据，往data列表的第一个列表也就是data[0]添加数据
                    data[(n_row-1)%18].append(float(r[i]))
                else:
                    data[(n_row-1)%18].append(float(0))
        n_row = n_row + 1
    text.close
    return data
    
"""
函数说明：
    解析保存好的训练数据集
参数：
    data - 训练集中所有数据，按污染物类别分为18个列表，都存储在data列表中
    每一行代表一个污染指标，每一行存储的是训练集中属于这个污染指标的所有的数据
返回值：
    trainX：
        trainX中的每一个列表（每一行）也就是存储的是data矩阵中的前9列，比如第一行是0~8列的所有data矩阵的数据，然
        后递推下去，第二行也是data矩阵中的前九列，但是初始索引不同而已变成了1~9
    trainY：
        #trainY中的每一个列表（每一行）存储的是data矩阵中的第9行，也就是PM2.5数据，
        但只存储第十个时刻，也就是从第九列开始的PM2.5的值，也就是存储的下一时刻的类推实际PM2.5的值，然后一直递推
"""
def Resolver_TrainData(data):
    # parse data to trainX and trainY。将列表数据解析为trainX和trainY
    x = []
    y = []
    for i in range(12):
        for j in range(471):
            x.append([])
            for t in range(18):
                for s in range(9):
                    x[471 * i + j].append(data[t][480 * i + j + s])  # 他只要前九列， 把data列表的1~18行0~8列，1~9，2~10.....，15-23,16-24....，分别存到他的x[0],x[1]...中.

            y.append(data[9][480 * i + j + 9])  # y存储的是data[9]也就是都是PM2.5的值，把第10行第10列，也就是存储的下一时刻的类推实际PM2.5的值
    trainX = np.array(x)  # 每一行有9*18个数 每9个代表9天的某一种污染物
    trainY = np.array(y)
    return trainX,trainY
    # print(len(x))#5652行
    # print(len(x[0]))#162列，他只要前九列，所以18*9=162
    # print(len(x[1]))#所以x存储的是data列表（也就是训练数据）的某九列的数据，把1~18行0~9列，1~10，2~11分别存到他的x[0],x[1]...中
    # print(len(y))#5652个数据，单行,存储的是训练数据中下一时刻的类推实际PM2.5的值
    # print(len(trainY))#在循环时，他会过掉10次，i=0时，9~479，i=1时479直接跳到489，差10，
    # 循环11次就差了10*10=100，然后减去第一次过掉的8个，所以就是5652

显然，在这里我们将csv中的所有数据集进行读取并以data数组进行保存，内有十八行，每行存储的都是每个污染指标的所有训练集。
然后通过Resolver_TrainData函数将训练集进行解析，对训练数据与相应训练集的预测值进行分离，通过trainX与trainY保存。

读取与解析测试集

读取测试集和读取训练集都是差不多意思，将我们要测试的数据与对应测试数据的测试值进行分离，最后用数组保存起来。但在我们这里，测试集数据与测试值是分开的.csv文件保存的，所以要再对其测试值的文件进行读取。
代码如下所示：

"""
函数说明：
    该函数用来分析测试数据
参数：
    空
返回值：
    test_x：
        test_x把每18行（也就是一个时间点）的数据全部加到test_x中的一行，
        然后再创另一行再加另外18行，也就是说test_x的每一行存储的是每一天的所有污染指标的前9个小时的数据
说明：
    test.csv内保存的是某一天前九个小时的18项污染指标的数据
    id_...表示第几天，每个id_...有18行，代表18项污染指标
    9个列代表测试用的前九个时刻
"""
def Read_TestingData():
    # parse test data分析测试数据
    # test_x把每18行（也就是一个时间点）的数据全部加到test_x中的一行，然后再创另一行再加另外18行，也就是说test_x的每一行存储的是每一天的所有污染指标的前9个小时的数据
    test_x = []
    n_row = 0
    text = open('data/test.csv', "r")
    row = csv.reader(text, delimiter=",")

    for r in row:
        if n_row % 18 == 0:
            test_x.append([])
            for i in range(2, 11):
                test_x[n_row // 18].append(float(r[i]))#//表示整数除法
        else:
            for i in range(2, 11):
                if r[i] != "NR":
                    test_x[n_row // 18].append(float(r[i]))
                else:
                    test_x[n_row // 18].append(0)
        n_row = n_row + 1
    text.close()
    test_x = np.array(test_x)
    return test_x

"""
函数说明：
    读取测试集测试的真实答案，也就是测试集中给出的每一天前九个小时的所有污染指标数据，所预测出的下一时刻PM2.5值
参数：
    空
返回值：
    存储某天这个时间点的PM2.5值    
"""
def Read_TestAnswer():
    #parse answer分析答案
    ans_y = []
    n_row = 0
    text = open('data/ans.csv', "r")
    row = csv.reader(text, delimiter=",")

    for r in row:
        ans_y.append(r[1])

    ans_y = ans_y[1:]
    ans_y = np.array(list(map(int, ans_y)))
    #print(ans_y[1])
    return ans_y

这就完美的将训练集与测试集读取出来了。

2.训练模型

在将数据集分离之后，就可以通过算法来训练模型啦，在这里我们将测试Adagrad自适应梯度算法与随机梯度下降算法对模型进行训练，并对比这两种算法，选择最好的那一种。如果对算法有不了解的，请回头看我的这两篇博文：

• https://blog.csdn.net/qq_42263553/article/details/103367986
• https://blog.csdn.net/qq_42263553/article/details/103367986

如果你明白梯度下降算法的回归，那么请直接看第二篇博文。
废话不多说，看看两种算法的代码：

#trainX:是x转换的数组然后与一个240行，1列的数组拼接后的数组, trainY：就是训练数据从第一天第九时刻开始的PM2.5值,
#w就是一个163个元素的全0数组（163是因为是复制的trainX数组的形式，
#而trainX数组是与一个240行1列的数组组合后的数组他默认有个1，所以拼接就是163），他就是实际的参数，初始状态默认参数为0进行梯度下降
#eta=1学习频率
#iteration=20000循环次数
#lambdaL2=0是规则化用的λ
"""
函数说明：
    Adagrad自适应梯度算法
    每隔一段时间就把学习速度降低一些。
    一开始，我们离目的地很远，所以我们使用更大的learning rates
    经过了一段时间，我们离目的地越来越近了，所以我们的learning rates要变小
    让每一个不同的参数都给他不同的learning rates。
    公式：η^t=η∕√(t+1)，用每次梯度下降求解的点所对应的的参数的learning rates除以之前算出来的偏微分值的均方根。
    
    问题：学习频率没调好可能会导致梯度下降找不到最低点
    好处：初始学习频率很大，经过一段时间快要到最低点的时候，学习频率会越来越变小。
"""
def ada(X, Y, w, eta, iteration, lambdaL2):
    s_grad = np.zeros(len(X[0]))#zeros数组：全零数组，元素全为零。
    list_cost = []
    for i in range(iteration):#20000次循环
        hypo = np.dot(X,w)#dot()返回的是两个数组的点积，w是一个163个元素的全零数组，对应公式看
        #print(hypo[0])初始为0
        loss = hypo - Y #用训练数据实际值与预测值数组相减，得到新数组，大小为5652，得到loss funcion，初始为一个负的Y数组。
        cost = np.sum(loss**2)/len(X)#sum方法：对参数求和。首先对Loss数组内的元素都进行平方，求和，再取平均值
        #对应Loss function的公式，得到Loss的值
        list_cost.append(cost)
        grad = np.dot(X.T, loss)/len(X) + lambdaL2*w
        s_grad += grad**2#对gt的求平方再累加
        ada = np.sqrt(s_grad)#ot
        w = w - eta*grad/ada#参数更新
    return w, list_cost#返回参数已经迭代的数组，返回已经迭代过的Loss列表

"""
函数说明：
    使用随机梯度下降法训练模型，随机梯度下降法功能是可以加快训练速度
    每次取一个xn出来，然后估测Loss function误差函数，更新w
"""
def SGD(X, Y, w, eta, iteration, lambdaL2):
    list_cost = []
    for i in range(iteration):
        hypo = np.dot(X,w)
        loss = hypo - Y
        cost = np.sum(loss**2)/len(X) #LossFunction的值
        list_cost.append(cost)

        rand = np.random.randint(0, len(X))
        grad = X[rand]*loss[rand]/len(X) + lambdaL2*w
        w = w - eta*grad
    return w, list_cost

"""
函数说明：
    使用普通梯度下降法训练模型
"""
def GD(X, Y, w, eta, iteration, lambdaL2):
    list_cost = []
    for i in range(iteration):
        hypo = np.dot(X,w)#点积
        loss = hypo - Y #Loss funcion内部解算
        cost = np.sum(loss**2)/len(X) #求出Loss funcion，平方然后再取平均值，因为训练数据有len(X)个
        list_cost.append(cost)
        #规则化操作
        grad = np.dot(X.T, loss)/len(X) + lambdaL2 * w #（修改Loss function：加入所有参数的平方和乘上λ）
        w = w - eta*grad
    return w, list_cost

在训练好模型之后，也就是得到最优参数解集w之后，我们可以用测试数据，对两种算法进行测试。

3.测试模型

接下来直接使用我们的测试数据与对应的最优参数解集相乘，看看测试集所对应的两种算法得出来的解。
代码如下：

#output testdata输出测试数据
y_ada = np.dot(test_x, w_ada)#ada方法：用测试数据和已经迭代完毕的参数进行演算测试数据y的值的集合。
y_sgd = np.dot(test_x, w_sgd)#sgd方法的
y_cf = np.dot(test_x, w_cf)#正确数据，#加入偏差之后的真实值

Save_Test_Result(w_ada)#选择测试效果最好的算法，将数据进行保存

def Save_Test_Result(w):
    # csv format  csv格式保存
    ans = []
    for i in range(len(test_x)):  # test_x是240行的对应240天
        ans.append(["id_" + str(i)])
        a = np.dot(w, test_x[i])  # 用训练数据得出的最好funcion的参数集合与测试数据做点积
        # 就是测试数据的结果
        ans[i].append(a)

    # 下面这几行是写入文件
    filename = "result/predict.csv"
    text = open(filename, "w+")
    s = csv.writer(text, delimiter=',', lineterminator='\n')
    s.writerow(["id", "value"])
    for i in range(len(ans)):
        s.writerow(ans[i])
    text.close()

可见，我们选择了ada算法，并对其测试集进行保存.csv文件，接下来我们要对比一下两个算法与真实值之间的差距，以此来判断哪种算法更好。
代码如下所示：

    #显示波形
    #plot training data with different gradiant method用不同梯度法绘制训练数据
    #plot第一个参数是x轴的数据，第二个参数是y轴数据，第三个是颜色，第四个是控制曲线的格式字符串
    """
    这部分是对自适应梯度下降算法与随机梯度下降算法中，训练过程的迭代次数与误差之间的关系曲线
    """
    plt.plot(np.arange(len(cost_list_ada[3:])), cost_list_ada[3:], 'b', label="ada")
    plt.plot(np.arange(len(cost_list_sgd[3:])), cost_list_sgd[3:], 'g', label='sgd')
    # plt.plot(np.arange(len(cost_list_sgd50[3:])), cost_list_sgd50[3:], 'c', label='sgd50')
    # plt.plot(np.arange(len(cost_list_gd[3:])), cost_list_gd[3:], 'r', label='gd')
    plt.plot(np.arange(len(cost_list_ada[3:])), hori, 'y--', label='close-form')
    plt.title('Training Process')
    plt.xlabel('Iteration')
    plt.ylabel('Loss function (quadratic)')
    plt.legend()
    plt.savefig(os.path.join(os.path.dirname(__file__), "figures/TrainProcess"))
    plt.show()

    #plot fianl answer
    plt.figure()#绘图
    plt.subplot(131)
    plt.title('CloseForm')
    plt.xlabel('dataset')
    plt.ylabel('pm2.5')
    plt.plot(np.arange((len(ans_y))), ans_y, 'r,')
    plt.plot(np.arange(240), y_cf, 'b')

    plt.subplot(132)
    plt.title('ada')
    plt.xlabel('dataset')
    plt.ylabel('pm2.5')
    plt.plot(np.arange((len(ans_y))), ans_y, 'r,')
    plt.plot(np.arange(240), y_ada, 'g')

    plt.subplot(133)
    plt.title('sgd')
    plt.xlabel('dataset')
    plt.ylabel('pm2.5')
    plt.plot(np.arange((len(ans_y))), ans_y, 'r,')
    plt.plot(np.arange(240), y_sgd, 'b')
    plt.tight_layout()
    plt.savefig(os.path.join(os.path.dirname(__file__), "figures/Compare"))
    plt.show()

好了，这三个步骤都做完了，也就完成了我们的预测目的。
想必上面的内容大家会看得头昏眼花，因为部分代码看不到效果，所以我将所有的代码进行了整理。

整体代码

import csv, os #导入系统库和csv库
import numpy as np #导入numpy库
import matplotlib.pyplot as plt
from numpy.linalg import inv
import random
import math
import sys

#trainX:是x转换的数组然后与一个240行，1列的数组拼接后的数组, trainY：就是训练数据从第一天第九时刻开始的PM2.5值,
#w就是一个163个元素的全0数组（163是因为是复制的trainX数组的形式，
#而trainX数组是与一个240行1列的数组组合后的数组他默认有个1，所以拼接就是163），他就是实际的参数，初始状态默认参数为0进行梯度下降
#eta=1学习频率
#iteration=20000循环次数
#lambdaL2=0是规则化用的λ
"""
函数说明：
    Adagrad自适应梯度算法
    每隔一段时间就把学习速度降低一些。
    一开始，我们离目的地很远，所以我们使用更大的learning rates
    经过了一段时间，我们离目的地越来越近了，所以我们的learning rates要变小
    让每一个不同的参数都给他不同的learning rates。
    公式：η^t=η∕√(t+1)，用每次梯度下降求解的点所对应的的参数的learning rates除以之前算出来的偏微分值的均方根。
    
    问题：学习频率没调好可能会导致梯度下降找不到最低点
    好处：初始学习频率很大，经过一段时间快要到最低点的时候，学习频率会越来越变小。
"""
def ada(X, Y, w, eta, iteration, lambdaL2):
    s_grad = np.zeros(len(X[0]))#zeros数组：全零数组，元素全为零。
    list_cost = []
    for i in range(iteration):#20000次循环
        hypo = np.dot(X,w)#dot()返回的是两个数组的点积，w是一个163个元素的全零数组，对应公式看
        #print(hypo[0])初始为0
        loss = hypo - Y #用训练数据实际值与预测值数组相减，得到新数组，大小为5652，得到loss funcion，初始为一个负的Y数组。
        cost = np.sum(loss**2)/len(X)#sum方法：对参数求和。首先对Loss数组内的元素都进行平方，求和，再取平均值
        #对应Loss function的公式，得到Loss的值
        list_cost.append(cost)
        grad = np.dot(X.T, loss)/len(X) + lambdaL2*w
        s_grad += grad**2#对gt的求平方再累加
        ada = np.sqrt(s_grad)#ot
        w = w - eta*grad/ada#参数更新
    return w, list_cost#返回参数已经迭代的数组，返回已经迭代过的Loss列表

"""
函数说明：
    使用随机梯度下降法训练模型，随机梯度下降法功能是可以加快训练速度
    每次取一个xn出来，然后估测Loss function误差函数，更新w
"""
def SGD(X, Y, w, eta, iteration, lambdaL2):
    list_cost = []
    for i in range(iteration):
        hypo = np.dot(X,w)
        loss = hypo - Y
        cost = np.sum(loss**2)/len(X) #LossFunction的值
        list_cost.append(cost)

        rand = np.random.randint(0, len(X))
        grad = X[rand]*loss[rand]/len(X) + lambdaL2*w
        w = w - eta*grad
    return w, list_cost

"""
函数说明：
    使用普通梯度下降法训练模型
"""
def GD(X, Y, w, eta, iteration, lambdaL2):
    list_cost = []
    for i in range(iteration):
        hypo = np.dot(X,w)#点积
        loss = hypo - Y #Loss funcion内部解算
        cost = np.sum(loss**2)/len(X) #求出Loss funcion，平方然后再取平均值，因为训练数据有len(X)个
        list_cost.append(cost)
        #规则化操作
        grad = np.dot(X.T, loss)/len(X) + lambdaL2 * w #（修改Loss function：加入所有参数的平方和乘上λ）
        w = w - eta*grad
    return w, list_cost

"""
函数说明：读取训练数据，用传入的列表进行保存
参数：
data - 用以保存整个训练集的数据的空列表，这个列表内部又包含18个列表，代表18项污染物指标
返回值：
data - 读取完训练集数据返回的列表，这个内部有18个列表，也就是十八行
每一行代表一个污染指标，每一行存储的是训练集中属于这个污染指标的所有的数据
"""
def Read_TrainData(data):
    #read data
    #读取训练数据，把训练数据都取出来用一个data列表，训练数据是每个月前20天每个小时的气象资料（每小时有18种测资）
    #列表中有18个小列表，小列表就是一个小项。代表有十八行
    #每个小列表里面有24*240=5760个数据，因为每18个项目后，下一个24列又从data[0]开始存
    n_row = 0
    text = open('data/train.csv', 'r', encoding='big5')
    row = csv.reader(text, delimiter=',')#使用csv读取表格
    for r in row: #row是一个迭代器，每次迭代一行
        if n_row != 0: #过滤第一行，因为都是名称，从第二行一直到最后一行
            for i in range(3,27):#从第二行的三列数据逐行读取，抛弃前面的无用项目
                if r[i] != "NR":#第二行的第三个数据，往data列表的第一个列表也就是data[0]添加数据
                    data[(n_row-1)%18].append(float(r[i]))
                else:
                    data[(n_row-1)%18].append(float(0))
        n_row = n_row + 1
    text.close
    return data

"""
函数说明：
    解析保存好的训练数据集
参数：
    data - 训练集中所有数据，按污染物类别分为18个列表，都存储在data列表中
    每一行代表一个污染指标，每一行存储的是训练集中属于这个污染指标的所有的数据
返回值：
    trainX：
        trainX中的每一个列表（每一行）也就是存储的是data矩阵中的前9列，比如第一行是0~8列的所有data矩阵的数据，然
        后递推下去，第二行也是data矩阵中的前九列，但是初始索引不同而已变成了1~9
    trainY：
        #trainY中的每一个列表（每一行）存储的是data矩阵中的第9行，也就是PM2.5数据，
        但只存储第十个时刻，也就是从第九列开始的PM2.5的值，也就是存储的下一时刻的类推实际PM2.5的值，然后一直递推
"""
def Resolver_TrainData(data):
    # parse data to trainX and trainY。将列表数据解析为trainX和trainY
    x = []
    y = []
    for i in range(12):
        for j in range(471):
            x.append([])
            for t in range(18):
                for s in range(9):
                    x[471 * i + j].append(data[t][480 * i + j + s])  # 他只要前九列， 把data列表的1~18行0~8列，1~9，2~10.....，15-23,16-24....，分别存到他的x[0],x[1]...中.

            y.append(data[9][480 * i + j + 9])  # y存储的是data[9]也就是都是PM2.5的值，把第10行第10列，也就是存储的下一时刻的类推实际PM2.5的值
    trainX = np.array(x)  # 每一行有9*18个数 每9个代表9天的某一种污染物
    trainY = np.array(y)
    return trainX,trainY
    # print(len(x))#5652行
    # print(len(x[0]))#162列，他只要前九列，所以18*9=162
    # print(len(x[1]))#所以x存储的是data列表（也就是训练数据）的某九列的数据，把1~18行0~9列，1~10，2~11分别存到他的x[0],x[1]...中
    # print(len(y))#5652个数据，单行,存储的是训练数据中下一时刻的类推实际PM2.5的值
    # print(len(trainY))#在循环时，他会过掉10次，i=0时，9~479，i=1时479直接跳到489，差10，
    # 循环11次就差了10*10=100，然后减去第一次过掉的8个，所以就是5652

"""
函数说明：
    该函数用来分析测试数据
参数：
    空
返回值：
    test_x：
        test_x把每18行（也就是一个时间点）的数据全部加到test_x中的一行，
        然后再创另一行再加另外18行，也就是说test_x的每一行存储的是每一天的所有污染指标的前9个小时的数据
说明：
    test.csv内保存的是某一天前九个小时的18项污染指标的数据
    id_...表示第几天，每个id_...有18行，代表18项污染指标
    9个列代表测试用的前九个时刻
"""
def Read_TestingData():
    # parse test data分析测试数据
    # test_x把每18行（也就是一个时间点）的数据全部加到test_x中的一行，然后再创另一行再加另外18行，也就是说test_x的每一行存储的是每一天的所有污染指标的前9个小时的数据
    test_x = []
    n_row = 0
    text = open('data/test.csv', "r")
    row = csv.reader(text, delimiter=",")

    for r in row:
        if n_row % 18 == 0:
            test_x.append([])
            for i in range(2, 11):
                test_x[n_row // 18].append(float(r[i]))#//表示整数除法
        else:
            for i in range(2, 11):
                if r[i] != "NR":
                    test_x[n_row // 18].append(float(r[i]))
                else:
                    test_x[n_row // 18].append(0)
        n_row = n_row + 1
    text.close()
    test_x = np.array(test_x)
    return test_x

"""
函数说明：
    读取测试集测试的真实答案，也就是测试集中给出的每一天前九个小时的所有污染指标数据，所预测出的下一时刻PM2.5值
参数：
    空
返回值：
    存储某天这个时间点的PM2.5值    
"""
def Read_TestAnswer():
    #parse answer分析答案
    ans_y = []
    n_row = 0
    text = open('data/ans.csv', "r")
    row = csv.reader(text, delimiter=",")

    for r in row:
        ans_y.append(r[1])

    ans_y = ans_y[1:]
    ans_y = np.array(list(map(int, ans_y)))
    #print(ans_y[1])
    return ans_y

def AddBias(trainX,test_x):
    # add bias 添加bias
    test_x = np.concatenate((np.ones((test_x.shape[0],1)),test_x), axis=1)#创建一个240行，1列的数组，与将test_x对应行进行拼接
    #concatenate能够一次完成多个数组的拼接。其中a1,a2,...是数组类型的参数,axis=1表示对应行的数组进行拼接
    #ones方法是创建一个全为1的数组，参数是一个元组，元组的第一个元素就是创建数组的行，第二个元素就是创建的数组的列
    trainX = np.concatenate((np.ones((trainX.shape[0],1)), trainX), axis=1)
    return trainX,test_x

def TrainModel(trainX,trainY):
    # train data 训练数据
    w = np.zeros(len(trainX[0]))  # 获取训练集的列数163列，w：1行，163列的0矩阵

    w_sgd, cost_list_sgd = SGD(trainX, trainY, w, eta=0.0001, iteration=20000, lambdaL2=0)#cost_list_sgd是每次迭代时保存的LossFunction值的列表
    # w_sgd50, cost_list_sgd50 = SGD(trainX, trainY, w, eta=0.0001, iteration=20000, lambdaL2=50)
    w_ada, cost_list_ada = ada(trainX, trainY, w, eta=1, iteration=20000, lambdaL2=0)
    # w_gd, cost_list_gd = SGD(trainX, trainY, w, eta=0.0001, iteration=20000, lambdaL2=0)

    # close form，closed form solution检查结果，标准答案
    w_cf = inv(trainX.T.dot(trainX)).dot(trainX.T).dot(trainY)#标准答案
    cost_wcf = np.sum((trainX.dot(w_cf) - trainY) ** 2) / len(trainX)
    hori = [cost_wcf for i in range(20000 - 3)]

    return w_sgd,cost_list_sgd,w_ada,cost_list_ada,w_cf,cost_wcf,hori

def Save_Test_Result(w):
    # csv format  csv格式保存
    ans = []
    for i in range(len(test_x)):  # test_x是240行的对应240天
        ans.append(["id_" + str(i)])
        a = np.dot(w, test_x[i])  # 用训练数据得出的最好funcion的参数集合与测试数据做点积
        # 就是测试数据的结果
        ans[i].append(a)

    # 下面这几行是写入文件
    filename = "result/predict.csv"
    text = open(filename, "w+")
    s = csv.writer(text, delimiter=',', lineterminator='\n')
    s.writerow(["id", "value"])
    for i in range(len(ans)):
        s.writerow(ans[i])
    text.close()

if __name__ == "__main__":
    # 每一个维度储存一种污染物的咨询，一共十八项污染物数据
    data = []
    #for循环18个列表添加到data列表中
    for i in range(18):
        data.append([])

    Traindata = Read_TrainData(data)

    trainX,trainY = Resolver_TrainData(Traindata)#trainX:5652行，162列 trainY:1行，5652列

    test_x = Read_TestingData()#240行、162列

    ans_y = Read_TestAnswer()#1行，240列

    trainX,test_x = AddBias(trainX,test_x)#加入偏差bias

    w_sgd,cost_list_sgd,w_ada,cost_list_ada,w_cf,cost_wcf,hori = TrainModel(trainX,trainY)

    #output testdata输出测试数据
    y_ada = np.dot(test_x, w_ada)#ada方法：用测试数据和已经迭代完毕的参数进行演算测试数据y的值的集合。
    y_sgd = np.dot(test_x, w_sgd)#sgd方法的
    y_cf = np.dot(test_x, w_cf)#正确数据，#加入偏差之后的真实值

    Save_Test_Result(w_ada)#选择测试效果最好的算法，将数据进行保存

    #print(len(cost_list_ada))#因为循环了20000次，所以有20000个Loss的结果都保存了起来
    #显示波形
    #plot training data with different gradiant method用不同梯度法绘制训练数据
    #plot第一个参数是x轴的数据，第二个参数是y轴数据，第三个是颜色，第四个是控制曲线的格式字符串
    """
    这部分是对自适应梯度下降算法与随机梯度下降算法中，训练过程的迭代次数与误差之间的关系曲线
    """
    plt.plot(np.arange(len(cost_list_ada[3:])), cost_list_ada[3:], 'b', label="ada")
    plt.plot(np.arange(len(cost_list_sgd[3:])), cost_list_sgd[3:], 'g', label='sgd')
    # plt.plot(np.arange(len(cost_list_sgd50[3:])), cost_list_sgd50[3:], 'c', label='sgd50')
    # plt.plot(np.arange(len(cost_list_gd[3:])), cost_list_gd[3:], 'r', label='gd')
    plt.plot(np.arange(len(cost_list_ada[3:])), hori, 'y--', label='close-form')
    plt.title('Training Process')
    plt.xlabel('Iteration')
    plt.ylabel('Loss function (quadratic)')
    plt.legend()
    plt.savefig(os.path.join(os.path.dirname(__file__), "figures/TrainProcess"))
    plt.show()

    #plot fianl answer
    plt.figure()#绘图
    plt.subplot(131)
    plt.title('CloseForm')
    plt.xlabel('dataset')
    plt.ylabel('pm2.5')
    plt.plot(np.arange((len(ans_y))), ans_y, 'r,')
    plt.plot(np.arange(240), y_cf, 'b')

    plt.subplot(132)
    plt.title('ada')
    plt.xlabel('dataset')
    plt.ylabel('pm2.5')
    plt.plot(np.arange((len(ans_y))), ans_y, 'r,')
    plt.plot(np.arange(240), y_ada, 'g')

    plt.subplot(133)
    plt.title('sgd')
    plt.xlabel('dataset')
    plt.ylabel('pm2.5')
    plt.plot(np.arange((len(ans_y))), ans_y, 'r,')
    plt.plot(np.arange(240), y_sgd, 'b')
    plt.tight_layout()
    plt.savefig(os.path.join(os.path.dirname(__file__), "figures/Compare"))
    plt.show()

抱歉有些地方也可以封装成一个独立的函数，但是我没有做了，大家可以整理一下。
接下来看一下效果，运行代码结果如下：

这是第一张图，从第一张图我们可以看出迭代次数和均方差（测试集的预测值与测试集的真实值的均方差）之间的关系，蓝色代表的是自适应梯度下降算法，绿色的代表的是随机梯度下降算法，而那根虚线close-form表示测试集真实值。

我们从图中可以看出自适应梯度下降算法效果明显要比随机梯度下降算法要好，从迭代次数可以知道，自适应梯度下降在迭代2500次左右就趋近与真实值，而随机梯度下降算法在迭代将近10000后才趋于平稳但与真实值还存在一定差距。另外从误差方面看，自适应梯度下降算法在迭代以后接近真实值，而随机梯度下降算法在迭代之后还存在一定误差，从这张图我们可以看出自适应梯度下降算法在这个数据集上要比随机梯度下降算法要好，但不能说自适应梯度下降算法就一定是最好，这要依据你的数据集来判别的。

除此之外，我们还将测试集真实值通过散点的形式在第二张图中展示，如下图所示：

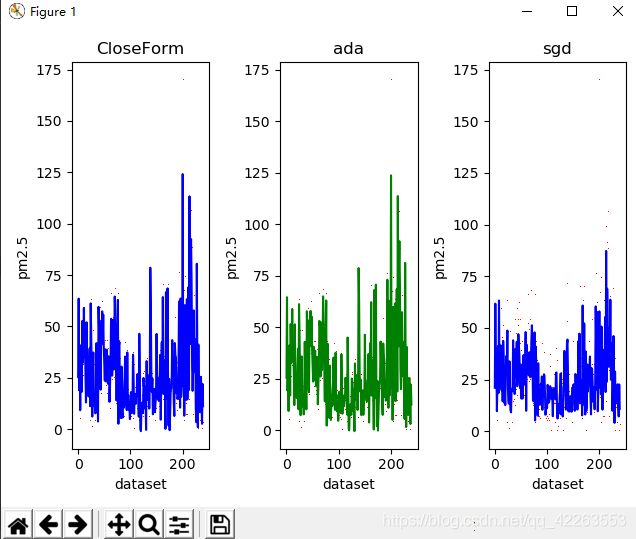
红色的点代表测试集的真实值，最左边那个图CloseForm，是加入bias偏差后的测试集的真实值，以这个作为标准，我们看中间的图，是使用自适应梯度下降算法对模型进行训练，然后对测试集进行预测的结果，是不是和最左边的很接近？答案是肯定的，然后最右边的图，也就是使用随机梯度下降算法对测试集预测的结果，与第一张图进行对比，差远了…
由此我们也可得出，使用自适应梯度下降算法对本实例的数据集所建立的模型进行预测，效果是最好的。

本人大三小白，因为疫情在家呆了半年，大半年前学的李宏毅老师的回归课程，这么久了难免会有知识点忘了，如果本文有错误或者不清楚的地方，还望大家原谅，指出我的错误之处，谢谢！我会继续改正与学习！