《机器学习实战》:非均衡分类问题(召回率/ROC/AUC/采样方法)
目录
- 1 正确率、召回率
- 2 ROC曲线及AUC
- 3 处理非均衡问题的数据抽样方法
分类不平衡问题是指,在一些分类问题中,我们关注的分类代价是不一样的。比前面章节中我们构建了一个用于检测患疝病的马匹是否存活的系统。假如某人给我们牵来一匹马,他希望我们能预测这匹马能否生存。,我们的分类器只有80%的精确率(accuracy)。 如果我们预测错误,那么我们将会错杀了一个如此昂贵的动物,更不要说人对马还存在情感上的依恋。这时我们肯定更希望不要错判。还有可能检测癌症时,患癌症的样本占比很少,可能只有1%,这是我们再用准确率衡量就会出现一些问题,比如我全部预测没有患癌症,则准确率就达到了99%,已经相当高了,但是这并不是我们想要的结果。
所以,针对非均衡分类问题,我们需要其他的衡量指标。
1 正确率、召回率
到现在为止,本书都是基于错误率来衡量分类器任务的成功程度的。错误率指的是在所有测试样例中错分的样例比例。实际上,这样的度量错误掩盖了样例如何被分错的事实。在机器学习中,有一个普遍适用的称为混淆矩阵(confusion matrix)的工具,它可以帮助人们更好地了解分类中的错误。有这样一个关于在房子周围可能发现的动物类型的预测,这个预测的三类问题的混淆矩阵如下表所示。

其中横着是真实的分类结果,纵着是预测的结果,混淆矩阵反应了分类结果的情况。利用混淆矩阵就可以更好地理解分类中的错误了。如果矩阵中的非对角元素均为0,就会得到一个完美的分类器。
为了简单起见,我们以二分类问题的混淆矩阵举例。下表是二分类问题的混淆矩阵。

在这个二类问题中:
如果将一个正例正确地判为正例,那么就可以认为产生了一个真正例(True Positive,TP,也称真阳);
如果对一个反例正确地判为反例,则认为产生了一个真反例(True Negative,TN,也称真阴);
如果对一个正例错误地判为反例,则认为产生了一个伪反例(False Negative, FN,也称假阴);
如果对一个反例错误地判为正例,则认为产生了一个伪正例(False Positive,FP,也称假阳)。
在分类中,当某个类别的重要性高于其他类别时,我们就可以利用上述定义来定义出多个比错误率更好的新指标。
第一个指标是正确率(Precision):等于TP/(TP+FP),给出的是预测为正例的样本中的真正正例的比例。
第二个指标是召回率(Recall),它等于TP/(TP+FN),给出的是预测为正例的真实正例占所有真实正例的比例。
我们可以很容易构造一个高正确率或高召回率的分类器,但是很难同时保证两者成立。如果将任何样本都判为正例,那么召回率达到百分之百而此时正确率很低。构建一个同时使正确率和召回率大的分类器是具有挑战性的。
2 ROC曲线及AUC
另一个用于度量分类中的非均衡性的工具是ROC曲线(ROC curve),ROC代表接收者操作特征(receiver operating characteristic),它早在二战期间由电气工程师构建雷达系统时使用过。 下图给出了一条ROC曲线的例子。
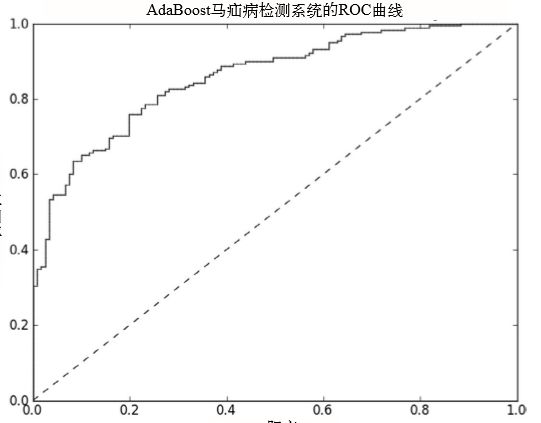
上面的ROC曲线中,给出了两条线,一条虚线一条实线。图中的横轴是伪正例的比例(假阳率=FP/(FP+TN)),而纵轴是真正例的比例(真阳率=TP/(TP+FN))。假设标签阳为1,阴为0,则:

ROC曲线给出的是当阈值变化时假阳率和真阳率的变化情况。阈值可以理解为最终模型判定分类的可能性,比如上一章AdaBoost算法的最终输出为sign(f(x)),这里的f(x)就可以理解为分类可能性或可信度。我们可以界定一个阈值,当f(x)大于多少时就分类为正例。左下角的点所对应的是将所有样例判为反例的情况,而右上角的点对应的则是将所有样例判为正例的情况。虚线给出的是随机猜测的结果曲线。
在理想的情况下,佳的分类器应该尽可能地处于左上角,这就意味着分类器在假阳率很低的同时获得了很高的真阳率。例如在垃圾邮件的过滤中,这就相当于过滤了所有的垃圾邮件,但 没有将任何合法邮件误识为垃圾邮件而放入垃圾邮件的文件夹中。
对不同的ROC曲线进行比较的一个指标是曲线下的面积(Area Unser the Curve,AUC)。AUC给出的是分类器的平均性能值,当然它并不能完全代替对整条曲线的观察。一个完美分类器的AUC为1.0,而随机猜测的AUC则为0.5。
那么怎么画ROC曲线呢?
1.把分类结果(即f(x))按照从小到大排序(从大到小也可以)。
2.依次按照上一步排序结果划分阈值。比如分类器结果为[0.3,0.5,0.6,0.7],当阈值为0.3时,最终分类结果为[0,0,0,0]全为负类,然后就可以计算真阳率和假阳率,下一个阈值为0.5,最终分类结果为[1,0,0,0],又可以计算真阳率和假阳率。依次遍历所有阈值,这样一个阈值就得到一个点。
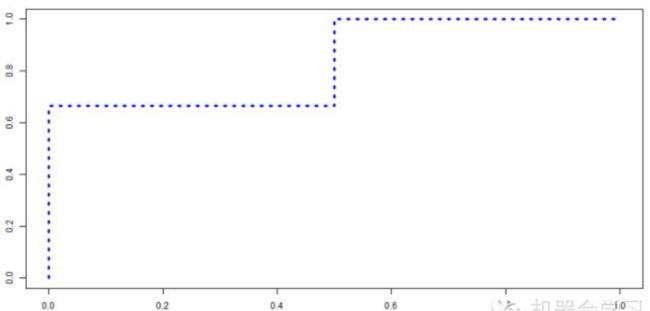
举例:
假如一个分类器预测样本为1的概率是p=c(0.5,0.6,0.55,0.4,0.7),真实的类别(标签)是y=c(1,1,0,0,1)。ROC计算过程如下:
1.对预测结果和标签排序
p=c(0.4,0.55,0.5,0.6,0.7),y=c(0,1,0,1,1)
2.划分阈值计算假阳率和真阳率

ROC曲线画出来如下:
那么代码如何写呢?
我们观察到每改变一个阈值,可以根据真实标签的情况来计算假阳率和真阳率。当前阈值的真实标签为1时,则说明计算真阳率的分子上少了1,分母为3永远不变,也就是的真阳率值减少了1/3,我们令1/3为每次减少的y轴步长,即1除以总1标签数量;同理,当前阈值的真实标签为0时,则说明计算假阳率的分子上少了1,分母为2永远不变,也就是的假阳率值减少了1/2,我们令1/2为每次减少的x轴步长,1除以总0标签数量。
那么如何计算AUC的值呢?
我们知道AUC是ROC曲线下的面积,我们可以把面积看作是一个个小的矩形。如下图,其中宽为x轴的步长,长为y轴的坐标值。并且只有x轴减少了,才会扩展出新的矩形宽。其中矩形的宽即x轴的步长是不变的,y轴是当x轴减少依次,我们就计算一次。最后面积为x1y1+x1y2=x1(y1+y2),其中x1为x轴的步长。

对应代码如下:
def plotROC(predStrengths, classLabels):
import matplotlib.pyplot as plt
cur = (1.0,1.0) #游标,也就是x和y轴坐标
ySum = 0.0 #计算AUC的y轴的总和
numPosClas = sum(np.array(classLabels)==1.0) # 1标签的数量
yStep = 1/float(numPosClas) # y轴的步长
xStep = 1/float(len(classLabels)-numPosClas) # x轴的步长
sortedIndicies = predStrengths.argsort()# 对分类器结果索引排序
fig = plt.figure()
fig.clf()
ax = plt.subplot(111)
for index in sortedIndicies.tolist()[0]: # 遍历所有结果,设不同的阈值
if classLabels[index] == 1.0: # 如果当前阈值索引下的真实标签为1,y轴减步长
delX = 0; delY = yStep;
else:
delX = xStep; delY = 0; # 如果当前阈值索引下的真实标签为0,x轴减步长
ySum += cur[1] # x轴左移,则把计算面积的y轴加上
#从 cur 到 (cur[0]-delX,cur[1]-delY)画线
ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY], c='b')
cur = (cur[0]-delX,cur[1]-delY) # 更新当前游标
ax.plot([0,1],[0,1],'b--')
plt.xlabel('False positive rate'); plt.ylabel('True positive rate')
plt.title('ROC curve for AdaBoost horse colic detection system')
ax.axis([0,1,0,1])
plt.show()
print ("the Area Under the Curve is: ",ySum*xStep)
测试代码:
# test5
datArr, labelArr = loadDataSet('horseColicTraining2.txt')
classifierArray,aggClassEst = adaBoostTrainDS(datArr, labelArr, 10)
plotROC(aggClassEst.T, labelArr)
图形结果如下:
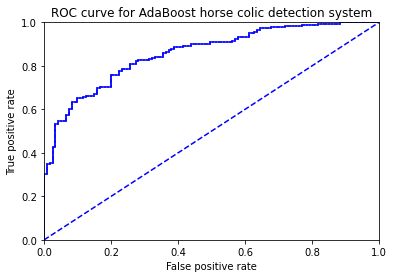
最后得到AUC为:the Area Under the Curve is: 0.8582969635063604。
这是在10个弱分类器下,AdaBoost算法性能的结 果。我们还记得,当初我们在50个弱分类器下得到了优的分类性能,那么这种情况下的ROC 曲线会如何呢?这时的AUC是不是更好呢? 经测试,当有50个弱分类器下,AUC为0.8953941870182941,相比10个有所提高。
3 处理非均衡问题的数据抽样方法
另外一种针对非均衡问题调节分类器的方法,就是对分类器的训练数据进行改造。这可以通过欠抽样(undersampling)或者过抽样(oversampling)来实现。。过抽样意味着复制样例,而欠抽样意味着删除样例。不管采用哪种方式,数据都会从原始形式改造为新形式。抽样过程则可以通过随机方式或者某个预定方式来实现。
通常也会存在某个罕见的类别需要我们来识别,比如在信用卡欺诈当中。如前所述,正例类别属于罕见类别。我们希望对于这种罕见类别能尽可能保留更多的信息,因此,我们应该保留正例类别中的所有样例,而对反例类别进行欠抽样或者样例删除处理。这种方法的一个缺点就在于要确定哪些样例需要进行剔除。但是,在选择剔除的样例中可能携带了剩余样例中并不包含的有价值信息。
上述问题的一种解决办法,就是选择那些离决策边界较远的样例进行删除。假定我们有一个数据集,其中有50例信用卡欺诈交易和5000例合法交易。如果我们想要对合法交易样例进行欠抽样处理,使得这两类数据比较均衡的话,那么我们就需要去掉4950个样例,而这些样例中可能包含很多有价值的信息。这看上去有些极端,因此有一种替代的策略就是使用反例类别的欠抽样和正例类别的过抽样相混合的方法。
要对正例类别进行过抽样,我们可以复制已有样例或者加入与已有样例相似的点。一种方法是加入已有数据点的插值点,但是这种做法可能会导致过拟合的问题。