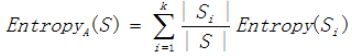机器学习实战——3决策树
文章对应《机器学习实战》第三章,为个人学习记录
主要是对各个函数的功能进行了比较易懂的描述,也可供python初学者参考。另外推荐机器学习实战代码注释,对在本书中入门python的同学应有很大帮助。
//计算给定数据集的香农熵
def calcShannonEnt(dataSet):
dataSet = [[1, 1, 'yes'],[1, 1, 'yes'],[1, 0, 'no'],[0, 1, 'no'],[0, 1, 'no']]
算出dataset中样本数量为5,新建字典A,按照dataset中最后一列的取值分类,累加出现次数
A[yes]=2,A[no]=3.根据熵计算公式将各个类别迭代求解
//划分数据集
def splitDataSet(dataSet, axis, value):
按照axis轴特征取值将dataSet分类,分类结果只保留特征值为value的项
若dataSet = [[1, 1, 'yes'],[1, 1, 'yes'],[1, 0, 'no'],[0, 1, 'no'],[0, 1, 'no']]
axis=0,value=1,则保留前三项,且舍去分类用特征值,返回结果[[1, 'yes'],[1, 'yes'],[0, 'no']]
//选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
初始化熵,外层循环遍历数据集的所有特征值以得到最优划分(最大的信息增益);内层循环根据当前特征值i划分数据集并求信息增益。
信息增益:假设划分前样本数据集为S,并用属性A来划分样本集S,则按属性A划分S的信息增益Gain(S,A)为样本集S的熵减去按属性A划分S后的样本子集的熵即
数据集S按照特征A划分后得到n个子集,求出各个子集熵并乘本子集权重,其和即为划分后的熵
//计算出现次数最多类别
def majorityCnt(classList):
输入为分类值['yes','yes','yes','no','no'],同求熵一样,建立字典A统计出现次数:A={'yes':3,'no':2}
按出现次数降序排序,返回A[0][0]=yes(另:A[0][1]=3)
//创建树的函数代码
def createTree(dataSet,labels):
此递归函数有两个退出条件:
1.数据集中分类均为yes或no,即都为同类
2.用于分类的特征均已使用,没有可再继续分类的依据,返回出现次数最多的类别
计算信息增益最大的划分特征,建立字典,将这个特征作为决策树原始根节点。
由于接下来将划分数据集,删去用于划分的特征,为了保证对应性在labels中删去最优特征标签
for循环递归建立决策树
循环变量value为最优划分特征的取值,如dataSet = [[1, 1, 'yes'],[1, 1, 'yes'],[1, 0, 'no'],[0, 1, 'no'],[0, 1, 'no']],若最优划分特征为0,即按照第0个元素划分,则value取值为1和0,使splitDataSet(dataSet, axis, value)能够得到所有的划分子集,后续的递归则在各个子集上进行.