189. Rotate Array

题目描述（简单难度）

转动数组，将数组的最后一个元素移动到开头，重复操作k次。

解法一

完全按照题目的意思，每次把末尾的元素移动到开头，当然移动前需要把所有元素后移一位，把第一个位置腾出来。

此外如果k大于数组的长度，k是等效于k % n的。举个例子，nums=[1 2 3 ],k=4,操作4次和操作4 % 3=1 次是一样的效果。

public class Rotate_Array {
    public static int[] rotate(int[] nums,int k) {
        int n=nums.length;
        k=k % n;
        for(int i = 0;i < k;i++) {
            int temp=nums[n-1];
            for(int j = n-1;j > 0;j--) {
                nums[j] = nums[j-1];
            }
            nums[0] = temp;
        }
        return nums;
    }
    public static void main(String args[]) {
        int[] nums = {1,2,3,4,5,6,6,7};
        int k = 3;
        int[] ans = rotate(nums,k);
        for(int i : ans){
            System.out.println(i);
        }
    }
}

时间复杂度：$O(\mathrm{k}\mathrm{n})$
空间复杂度：$O(1)$

解法二

空间换时间，解法一中每个元素都需要移动k次，因为最后一个元素移动到第一个位置的话，就进行了整体后移。不然的话，第一个位置原来的数就会被覆盖掉。

我们可以申请一个和原数组等大的数组，复制之前的所有的值。这样的话，我们就可以随心所欲的在原数组上赋值了，不需要考虑值的丢失。

public class Rotate_Array2 {
    public static int[] rotate(int[] nums,int k) {
        int n = nums.length;
        k = k % n;
        int[] numscopy =new int[n];
        for (int i = 0;i < n; i++){
            numscopy[i] = nums[i];
        }
        //末尾的 k 个数复制过来
        for (int i = 0;i < k; i++) {
            nums[i] = numscopy[n-k+i];
        }
        for (int i = k;i < n;i++) {
            nums[i] = numscopy[i - k];
        }
        return nums;
    }
}

时间复杂度：$O(\mathrm{n})$
空间复杂度：$O(\mathrm{n})$

解法三

上面的解法都是可以直接想到的，我们来看下官方提供的解法。

换一种题目的理解方式。

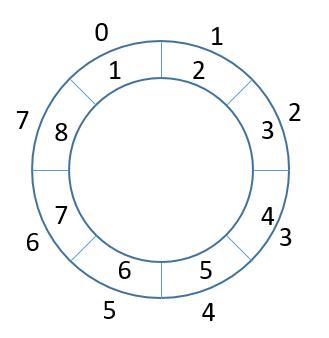
把数组看成一个圆环，而k的含义其实就是所有数组顺时针移动k个位置。

如果k=2，那么含义就是1放到3的位置，3放到5的位置…

当然程序上，如果1放到3的位置，3就会被覆盖了，我们应该用一个变量pre存储当前位置被占用的数字。

思想就是这样，我们来看下代码。

public void rotate(int[] nums, int k) {
    int n = nums.length;
    k = k % n;
    if (k == 0) {
        return;
    }
    int count = 0; //记录搬移了多少个数字
    int start = 0;
    int current = start;
    int pre = nums[current];
    while (true) {
        do {
            //要移动过去的位置
            int next = (current + k) % n;
            //数字做缓存
            int temp = nums[next];
            //将数字搬过来
            nums[next] = pre;
            pre = temp;
            //考虑下一个位置
            current = next;
            count++;
            //全部数字搬移完就结束
            if (count == n) {
                return;
            }
        } while (start != current);
        //这里是防止死循环，因为搬移的位置可能会回到最开始的位置, 所以我们 start++, 继续搬移其他组
        start++;
        current = start;
        pre = nums[current];
    }
}

时间复杂度：$O(\mathrm{n})$，每个数字仅搬移一次。
空间复杂度：$O(1)$

解法四

看具体的例子，1 2 3 4 5，k = 2。

转换后最终变成 4 5 1 2 3。

其实可以分三步完成。

整体逆序 5 4 3 2 1 。

前 k 个再逆序 4 5 3 2 1。

后边的再逆序 4 5 1 2 3。

public void rotate(int[] nums, int k) {
    int n = nums.length;
    k = k % n;
    reverse(nums, 0, n - 1);
    reverse(nums, 0, k - 1);
    reverse(nums, k, n - 1);
}

private void reverse(int[] nums, int start, int end) {
    while (start < end) {
        int temp = nums[start];
        nums[start] = nums[end];
        nums[end] = temp;
        start++;
        end--;
    }
}

时间复杂度：$O(\mathrm{n})$。
空间复杂度：$O(1)$。

总结

解法一、解法二就是对题目最简单的理解，解法三和解法四是进一步对题目的剖析，很厉害。

参考文献

• https://zhuanlan.zhihu.com/p/95998221
• https://leetcode-cn.com/problems/rotate-array/solution/xuan-zhuan-shu-zu-by-leetcode/