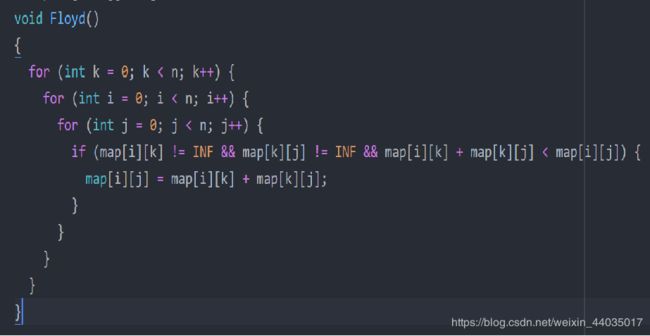
单源最短路径Dijkstra+多源最短路Floyed
图论起源于著名的哥尼斯堡七桥问题。在哥尼斯堡的普莱格尔河上有七座桥将河中的岛及岛与河岸联结起来。
问题是要从这四块陆地中任何一块开始,通过每一座桥正好一次,再回到起点。然而无数次的尝试都没有成功
欧拉在1736年解决了这个问题,他用抽像分析法将这个问题化为第一个图论问题:即把每一块陆地用一个点来代替,将每一座桥用联接相应的两个点的一条线来代替,从而相当于得到一个“图”。
欧拉证明了这个问题没有解,并且推广了这个问题,给出了对于一个给定的图可以某种方式走遍的判定法则。这就是后来的欧拉路径和欧拉回路。
欧拉回路
若图G中存在这样一条路径,使得它恰通过G中每条边一次,则称该路径为欧拉路径。若该路径是一个圈,则称为欧拉(Euler)回路。
定理:
(一)一个图有欧拉回路当且仅当它是连通的且每个顶点都有偶数度。
(二)一个图有欧拉通路当且经当它是连通的且除两个顶点外,其他顶点都有偶数度。
单源最短路径
从一个点出发,到达其他顶点的最短路径的长度。
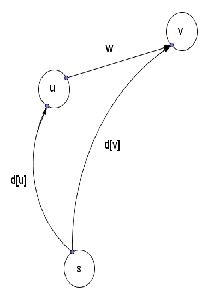
基本操作:松弛
d[u]+map[u, v]< d[v]这样的边(u,v)称为紧的(tense),可以对它进行松弛(relax):
d[v] = d[u]+w, pred[v] = u
最开始给每一个点一个很大的d值从d[s]=0开始,不断的对可以松弛的点进行松弛,不能松弛的时候就已经求出了最短路了
Dijkstra算法
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止
注意该算法要求图中不存在负权边。
可以证明,具有最小的d[i](临时最短路)值的(还没加入最短路)点在此以后无法松弛
所以每次找最近的点进行松弛操作
思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。


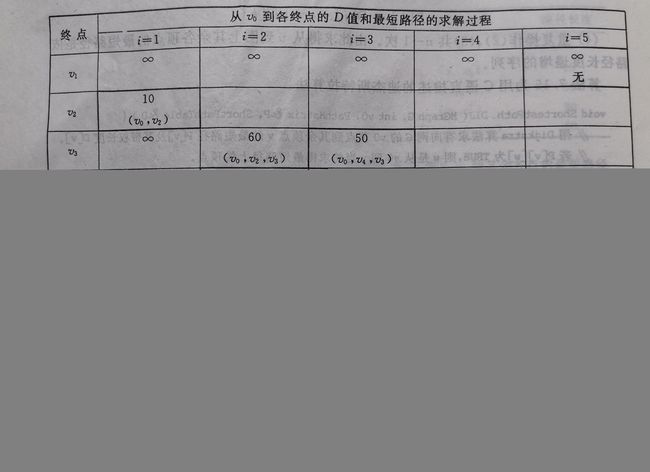
Dijkstra 算法不适用于带负权的图
当把一个点选入集合S时,就意味着已经找到了从A到这个点的最短路径,比如第二步,把C点选入集合S,这时已经找到A到C的最短路径了,但是如果图中存在负权边,就不能再这样说了。比如A到C的权值是7,A到B的权值是8,B到C的权值是-3,但是Dijkstra根据贪心的思想,选择与A最接近的点C,长度为7,以后不再变化。但是很明显此图最短路为5。归结原因是Dijkstra采用贪心思想,不从整体考虑结果,只从当前情况考虑选择最优。
问题 A: 简单最短路
时间限制: 1 Sec 内存限制: 128 MB
提交: 56 解决: 38
[提交][状态][讨论版][命题人:201806060121]
题目描述
老左今天打算去小寨逛街,但是呢作为一个新时代的年轻人他决定一定要找到最短的一条路,作为一个有钱的大佬,他认为公交车转车都是小钱,时间才是最重要的,于是他想知道最少要多少时间才能到小寨
假设一共有n 个车站,我们学校门口的车站编号为1, 小寨站编号为n,之后会给出一个m,随后会给出m条双向通道以及通过所需要的时间。
输入
第一行N , M ( 2 <= N <= 1000 1 <= M <= 2000)
第二行到第M+ 1行,三个数字a , b , c 表示a 站点到b 站点有一条路,需要 c min
输出
一行表示他需要的最少时间
样例输入
5 5
1 2 20
2 3 30
3 4 20
4 5 20
1 5 100
样例输出
90
这就是一个模板题 模板代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=1005;
const int INF=0x3f3f3f3f;
int Map[maxn][maxn],dis[maxn],check[maxn];
//Map数组存邻接矩阵 dis数组存起点到下标点的最短路径,check表示是否加入S集合
int Dis(int n,int m){
memset(dis,0,sizeof(dis));
memset(check,0,sizeof(check));
for(int i=1;i<=n;i++)
dis[i]=Map[1][i]; //本题起点为1,所以初始化dis为点1到其他点的最短路径为邻接矩阵上的点1到其他点的值
check[1]=1,dis[1]=0;//点1是起点,所以dis[1]=0
int minx=0,pos; //pos存比较后的最短路径的下标
for(int i=1;i<n;i++){ //遍历n-1次,每一次找出最短路径
minx=INF;//申请一个用于比较的变量
for(int j=1;j<=n;j++){ //遍历n个点找出最短路径点
if(!check[j]&&minx>dis[j]){
minx=dis[j];
pos=j;
}
}
check[pos]=1; //加入S集合
for(int j=1;j<=n;j++){ //更新,进行松弛操作,也就是比较起点1直接到点j和起点1通过pos点到点j的距离,如果起点1通过pos点到点j的距离更小则更新这个距离
if(!check[j]&&dis[j]>dis[pos]+Map[pos][j]){
dis[j]=dis[pos]+Map[pos][j];
}
}
}
return dis[n];//最后返回终点的dis值,因为此题中n是终点,所以返回dis[n]
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++) //初始化邻接矩阵
Map[i][j]=INF;
int a,b,c;
for(int i=1;i<=m;i++){
cin>>a>>b>>c; //输入值
Map[a][b]=Map[b][a]=c;
}
cout<<Dis(n,m)<<endl;
}
问题 B: 旅游的红红
时间限制: 1 Sec 内存限制: 128 MB
题目描述
这个暑假红红想去福建旅游,他打算来个自由浪漫行,但是为了省钱,他决定走花费最小的路线
红红已经研究过了把自己从西安运送到福建的路线。这些路线包括起始点和终点先一共经过T(1<=T<=2500)个城镇,方便地标号為1到T。除了起点和终点外地每个城镇由两条双向道路连向至少两个其它地城镇。每条道路有一个通过费用(包括油费,过路费等等)。
给定一个地图,包含m(1<=m<=6200)条直接连接2个城镇的道路。每条道路由道路的起点Rs,终点Re(1<=Rs<=T;1<=Re<=T),和花费(1<=Ci<=1000)组成。求从起始的城镇Ts(1<=Ts<=T)到终点的城镇Te(1<=Te<=T)最小的总费用。
输入
第一行: 4个由空格隔开的整数: T m Ts Te
第2到第C+1行: 第i+1行描述第i条道路。有3个由空格隔开的整数: Rs Re和Ci
输出
一个单独的整数表示从Ts到Te的最小总费用。数据保证至少存在一条道路。
样例输入
7 11 5 4
2 4 2
1 4 3
7 2 2
3 4 3
5 7 5
7 3 3
6 1 1
6 3 4
2 4 3
5 6 3
7 2 1
样例输出
7
提示
5->6->1->4(3+1+3)
这个题和上个题是一样的,不同的是起点和终点不在是1和n,所以只需要稍稍改变一下就行
#include<bits/stdc++.h>
using namespace std;
const int maxn=2500+5;
#define INF 0x3f3f3f3f
int Map[maxn][maxn],dis[maxn],check[maxn];
int Dis(int n,int m,int start,int end){
memset(dis,0,sizeof(dis));
memset(check,0,sizeof(check));
for(int i=1;i<=n;i++)
dis[i]=Map[start][i]; //初始化起点到其他点的值为邻接矩阵的值
check[start]=1,dis[start]=0; //起点加入S集合 dis起点值命为0
int minx=0,pos;
for(int i=1;i<n;i++){ //下面跟上面的题一样
minx=INF;
for(int j=1;j<=n;j++){
if(!check[j]&&minx>dis[j]){
minx=dis[j];
pos=j;
}
}
check[pos]=1;
for(int j=1;j<=n;j++){
if(!check[j]&&dis[j]>dis[pos]+Map[pos][j])
dis[j]=dis[pos]+Map[pos][j];
}
}
return dis[end]; //最后返回终点的dis值
}
int main(){
int n,m,start,end;
cin>>n>>m>>start>>end;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
Map[i][j]=INF;
int a,b,c;
for(int i=1;i<=m;i++){
cin>>a>>b>>c;
if(Map[a][b]>c)//这是一个去重边的操作
Map[a][b]=Map[b][a]=c;
}
cout<<Dis(n,m,start,end)<<endl;
}
v
多源最短路—Floyed
弗洛伊德算法用来解决全源最短路问题,即对给定的图G(V,E),求任意两点之间的最短路径问题,时间复杂度O(n^3)。
由于n^3的复杂度决定了顶点数n限制在200以内,因此用邻接矩阵来实现Floyd算法是非常适合的。
基于这样一个事实:如果存在顶点k,使得k作为中介点时,顶点i和顶点j的当前距离缩短,则使用k作为顶点i和顶点j的中介点。
Floyed-Warshall 算法用来找出每对点之间的最短距离。它需要用邻接矩阵来储存边,这个算法通过考虑最佳子路径来得到最佳路径。 是一个经典的动态规划算法,注意单独一条边的路径也不一定是最佳路径。
它可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包
设图有 n 个顶点,边号分别为 1,2,…,n。,对于其中三个顶点 k,i,j,若 p 是从 i 到 j 的一条最短路径,且满足路径中所有节点的编号都小于等于 k。
如果 k 节点在路径 p 中没有出现,那么 p 的所有中间节点的编号便都在 1~k-1 范围内。
如果 k 在路径 p 中出现过,则该路径包含 i~k 与 k~j 两部分,两部分路径的节点除端点外均不大于 k-1
得到 i~j 的途经顶点不大于 k 的最短路径的一个选择方法,假设使用g[k][i][j]来表示 i~j 途经顶点不超过 k 的最短距离,则 g[k][i][j]=min(g[k-1][i][j],g[k-1][i][k]+g[k-1][k][j])。
在决定途经顶点不超过 k 时每对顶点间的最短距离时只需要途经顶点不超过 k-1时每对顶点间的最短距离,只需要将上式改为:
g[i][j]=min(g[i][j],g[i][k]+g[k][j])
int i,j,k;
for(k=1; k<=n; k++)
for(i=1; i<=n; i++)
for(j=1; j<=n; j++)
g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
//g为图的邻接矩阵
A*
A算法,A(A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法,也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近,最终搜索速度越快。
A* (A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法,也是许多其他问题的常用启发式算法。注意——是最有效的直接搜索算法
公式表示为: f(n)=g(n)+h(n),
其中, f(n) 是从初始状态经由状态n到目标状态的代价估计,
g(n) 是在状态空间中从初始状态到状态n的实际代价,
h(n) 是从状态n到目标状态的最佳路径的估计代价
该算法在最短路径搜索算法中分类为:
直接搜索算法:直接在实际地图上进行搜索,不经过任何预处理
启发式算法:通过启发函数引导算法的搜索方向;
静态图搜索算法:被搜索的图的权值不随时间变化(后被证明同样可以适用于动态图的搜索
我们以d(n)表达状态n到目标状态的距离,那么h(n)的选取大致有如下三种情况:
如果h(n)< d(n)到目标状态的实际距离,这种情况下,搜索的点数多,搜索范围大,效率低。但能得到最优解。
如果h(n)=d(n),即距离估计h(n)等于最短距离,那么搜索将严格沿着最短路径进行, 此时的搜索效率是最高的。
如果 h(n)>d(n),搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
启发式函数h(n)告诉A从任意结点n到目标结点的最小代价评估值。选择一个好的启发式函数是重要的。
启发式函数可以控制A的行为:
一种极端情况,如果h(n)是0,则只有g(n)起作用,此时A演变成Dijkstra算法,这保证能找到最短路径。
另一种极端情况,如果h(n)比g(n)大很多,则只有h(n)起作用,A演变成BFS算法。
所以我们可以决定我们想要从A中获得什么。理想情况下,我们想最快地得到最短路径。如果我们的目标太低,我们仍会得到最短路径,不过速度变慢了;如果我们的目标太高,那我们就放弃了最短路径,但A运行得更快。