Bezier(贝塞尔)曲线的轨迹规划在自动驾驶中的应用(二)

根据（一）中的理论前提，我们通过matlab进行一次仿真验证：

clc
 clear all
 
 p0 = [ 0, 0];
 p1 = [10,0.5];
 p2= [20,3.5];
 p3 = [30,4];
 %设置控制点
 i =1;
 for u =0: 0.01:1
 p(i,:)= (1-u)^3*p0 + 3*(1-u)^2*u*p1 + 3*(1-u)*u^2*p2 + u^3*p3;
 i =i+1;
 end
 %生成三阶贝塞尔曲线的笛卡尔坐标系点位
 
 for i = 1:100 
 pd(i) = (p(i+1,2)-p(i,2))/(p(i+1,1)-p(i,1));
 pd(101) = 0;
 end
 %计算一阶导数
 for i =2: 100
     pdd(1) = 0;
     pdd(101) = 0;
     pdd(i) = (p(i+1,2)-2*p(i,2) + p(i-1,2))/(0.5*(-p(i-1,1)+p(i+1,1)))^2;
 end
 %计算二阶导数
 figure
 plot(1:101,pd);
figure
 plot(1:101, pdd);
 
 for i  = 1:101
     k(i) = (pdd(i))/(1+pd(i)^2)^(1.5);
 end
 figure
 plot(1:101,k)
 
 figure
 for i = 1: length(p)
 plot (p(i,1),p(i,2),'-o')
 hold on
 drawnow
 end           
 %%
 clc
 clear all
  p0 = [ 0, 0];
 p1 = [7.5,0];
 p2= [15,0];
 p3 = [15,4];
 p4 = [22.5,4];
 p5 = [30,4];
  %生成五阶贝塞尔曲线的笛卡尔坐标系点位
  i =1;
 for u =0: 0.01:1
 p(i,:)= (1-u)^5*p0 + 5*(1-u)^4*u*p1 + 10*(1-u)^3*u^2*p2 +...
     10*(1-u)^2*u^3*p3 +5*(1-u)*u^4*p4 + u^5*p5;
 i =i+1;
 end
 
 for i = 1:100 
 pd(i) = (p(i+1,2)-p(i,2))/(p(i+1,1)-p(i,1));
 pd(101) = 0;
 end
  %计算一阶导数
 for i =2: 100
     pdd(1) = 0;
     pdd(101) = 0;
     pdd(i) = (p(i+1,2)-2*p(i,2) + p(i-1,2))/(0.5*(-p(i-1,1)+p(i+1,1)))^2;
 end
  %计算二阶导数
 figure
 plot(1:101,pd);
figure
 plot(1:101, pdd);
 
 for i  = 1:101
     k(i) = (pdd(i))/(1+pd(i)^2)^(1.5);
 end
 figure
 plot(1:101,k)
 
 figure
 for i = 1: length(p)
 plot (p(i,1),p(i,2),'-o')
 hold on
 drawnow
 end

三次和五次曲线的形状是有差别的：

三次曲线

五次曲线

进一步的，分析曲线曲率，可以看出五次曲线的连续性更加平缓：

三次曲线

五次曲线

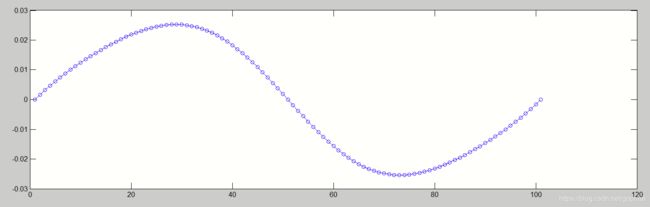
对于车辆来说，平滑的曲率意味着平滑的车辆转角控制，也意味着平滑的方向盘转角控制。因此，在变道路径规划中，更推荐 使用五阶贝塞尔曲线。