进阶无人驾驶—百度Apollo规划技术介绍

basic motion planning and overview

轨迹规划概览

一、What is motion planning

通俗解释：一个搜索问题，对于当前最优的状态进行搜索，怎么样去移动的一个最优解。而这个最优值我们会去用一个函数f(x)去定义它，我们通过数学计算来确定它的最优值。

上面是不同的领域所涉及的规划问题的不同方法和思想核心。当然我们都是把问题抽象化，去寻找最优值才简单。

比如我举个寻找下一个点的例子，并且使用广度优先算法的思想去寻找它：

Y可以看到，它的思想就是在绿色的起点处，不断向外扩张领域，直到碰到终点后，结束搜索，而这次寻找花费了6.4毫秒，好是花费了很长的时间了。

接着我们看看A*算法的搜索情况：

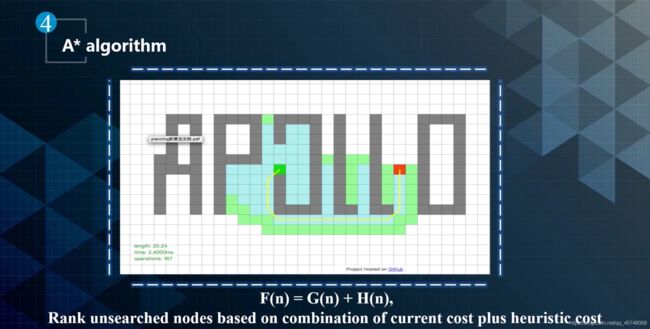
首先可以看到它的搜索步骤就变得很少了，没有上面的搜索那么复杂，而且还提高了不少的计算效率。可以看到它的下面有个算法公式，它的G（n）就是实际代价，也就是它走出去多远，花费的代价。而它的H（n）就是估计代价，也就是估算到终点的代价。

举个例子：

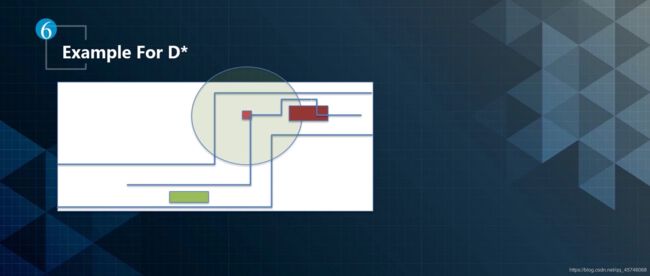
可以看到，红色小点是汽车，大块的红色和绿色是障碍物，当然是静态的，减少复杂度嘛。然后小车想沿着小路通过，并且躲避障碍物，那么它使用最优的A*算法行不行？

当然不可以啊，A*算法适用于全局搜索，也就是知道全局所有的信息的时候，去使用它才最好，如果你不知道全局信息就很难使用它。但是总得想个办法，于是想到了贪心算法，这就很贴近我们要求搜索了，想了解贪心算法得原理，可以自己详细学习哦。

当然我们继续分析上述得问题，就是无人车在通过一段路时，如何决策得问题。你可以看到车在拐弯的时候是直角，直来直去的，你觉得可能性大吗？显然不符合汽车的常量嘛，轮子360°无死角旋转都很难做到。

当然我们需要的是一个很适合驾驶和体验的平滑感觉，所以路也是需要有一定的平滑曲线作支撑的。那么我们不仅需要研究其规划模型，而且还需要考虑其运动模型，也确保规划模型是最优的。

难题之处

上面提到了对于静态障碍物的规划，那么其实在汽车行驶时，遇到的很多都是动态障碍物，所以我们需要去面对动态障碍物的避障问题。这就比静态障碍物更难去处理，但是又不得不去处理的地方了。

在处理之前我们需要干什么呢？我认为应该把交通规则注入无人车的灵魂中去，因为需要让无人车也去遵守大家都在遵守的一个规则，这样才会维护道路秩序，确保行车安全。

算的能否在最短的时间内得出最优的算法，确保在安全问题发生之前处理掉一个汽车应该处理的问题，才会让无人车赶超人类驾驶的方式。

可以看到这里面有很多感知模块，都是对信息采集的过程的描述。其中动态信息就是你当前的位置和状态，另一边静态信息主要就是地图信息带给我们的资源。

当然我们就需要了解一下这些系统的模块都是怎么去工作的。

module	question
Localization	Where we are
Perception	What we see
Prediction	How the environment will change
Motion Planning	How we move
Control	How to control the car

最后我们对本小节课程做个总结：

二、motion planning with autonomous driving

首先我们就以下几个方面入手，对我们的规划模块做一个学术的学习，以便更加了解我们的这个模块。

当然在不断的学习和研究后，相应的成果也纷纷面世，向着无人车技术的更高更难得领域前进，这也是一个奋斗不息得年代。

可以看到这些成果都很多，在相应的技术上也有一定的不可替代性。当然了我们还需要更多的技术去支持我们的无人驾驶技术更好的运行。

例如下图：

当无人车在行驶时，会把上面的路径当成一个一个的点去处理，而这些点又包含了许多有用的信息，比如说坐标等等。我们得到了这样的变量后就很容易把实际问题变得抽象化数学化了。

接着我们设想一下如何去定义汽车行驶时的平滑度，也就是汽车转弯时的曲率是否连续，有人就提出来了一个设想：从A点到达B点，我们对A，B两点都取一个10米长的半径，当汽车从A点出发时，贴着圆边走，直到看见B圆后走直线。接近B的圆边后，贴着圆边走，就会产生一个类似圆滑的路径。但是它经过计算发现，曲率却是不连续的，所以这样的简单想法，只是说是迈出了一步，但没有实际作用。

我们去解决一些问题，当然是把他们简单化，这样不断通过变换离散和连续，就能对问题继续处理了。

为了使问题简单化，我们可以利用其中的一个PRM，就是通过对环境中的两个点进行路径规划，你得到了一个地图的图片，需要对其数据进行离散化，以便简单处理。于是就想到一个办法，通过随机撒点，只要点在范围内就保留，否则抹去。然后连接这些点，找出最优值，当然这就需要A*算法的介入了。

当然在随机撒点时，会遇到两点连不上的情况，有可能是被障碍物阻挡，所以就不能成功的连接两点。所以我们需要对撒点和连线进行优化，例如平滑连线的记录和计算，都能提高规划效率。

例如上面的图我们把它分成两个方面进行优化，Path和Speed方面，就会将高维的问题简化低维的数据去处理。

当然这种算法也是有很多缺点的，例如计算得到的平滑曲线也不够理想。也有人提出先优化，再撒点等方法进行改进。这些方法的改进也是有局限的。也有二次优化的提出，这种算法在空间中有非常非常快的速度，但是它要求曲线是凸的，所以很难达到汽车需要的曲线，而是一味满足算法要求。

于是我们可以对上述的优化做一个简单的总结如下：

三、motion planning with environment-1

我们先抛出这样的研究模块，然后通过对这个模块的学习，再去细细的通过模块化的学习来了解问题。首先我们对汽车整体的技术模块进行了解：

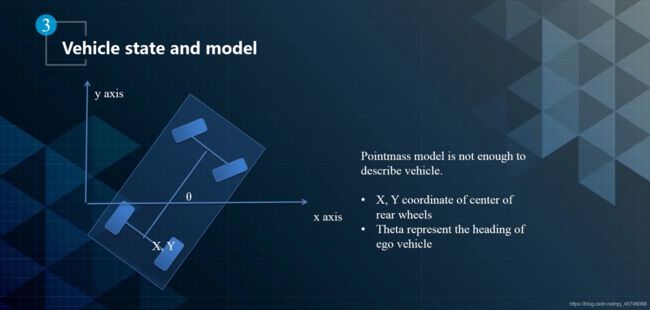
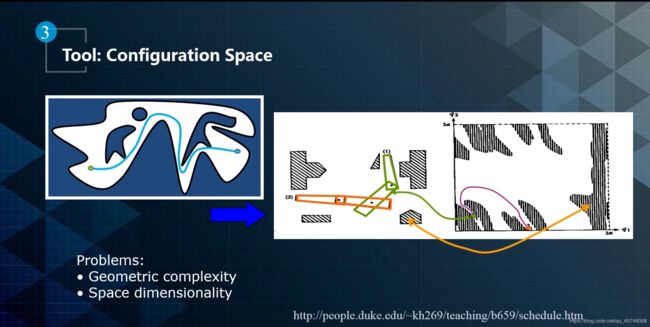
我们将汽车作为一个刚体，研究其车身朝向，朝向又会衍生自由度和角度等属性，来展示汽车的行驶属性。

可以将汽车运动模型简化为自行车模型，将四轮抽象成两个轮子，前轮中心和后轮中心的运动方向和自行车一样。车辆在垂直方向的运动被忽略掉，用一个二维平面上的运动物体来描述车辆的运动模型。自行车运动的时候具有以下特点，旋转车头的时候，前轮和后轮都围绕一个中心点转动，并且后轮的转向半径与方向盘转动角度满足以下关系，其中L为前轮中心和后轮中心的距离。

我们知道再转向时，前轮的半径和后轮的转向半径是有关联的，而不是相互之间没有关联的。而整个转向半径又是和后轮的转向半径有关系的，所以我们必须对后轮的研究进行学习。

如何去表示一个曲线的路径走向呢？单单依靠其角度走向是不能解决问题的。

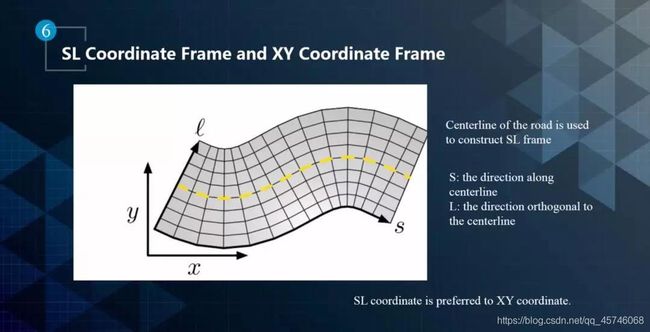
我们必须依靠这样一个坐标系的表示方法对其详细的说明。这样一个曲线可以通过图中所示的方程去表示，而其表示的过程也是比较复杂的，必须找出其在坐标系下的关系，通过关系的关联找出其方程表示，当然坐标系不但可以使用XY坐标系，也可以使用SL坐标系。

当然在对其进行算法计算时，必须考虑其精度和可行性，因为汽车在转向时必须严格考虑其行进过程中会出现类似于行人等情况，所以转向半径不能为了取得最优值而忽略道路行驶的可行性。

上面提到了SL坐标，SL坐标系也叫做frenet frame，如下所示。它以道路中心线为参考，S表示道路中心线的方向，L表示与道路中心线垂直的方向。在结构化道路上行驶的时候，SL坐标系比XY坐标系更加贴合实际需求。那么SL坐标系如何转换到XY坐标系呢？

四、motion planning with environment

在自动驾驶中，我们将环境抽象成 SL 坐标系，在此坐标系下的曲线光滑度是有要求的。首先，曲线本身要平滑。其次，其曲率也要满足平滑的特性。因此需要对轨迹线进行平滑处理。那么能不能先生成一条线，然后再进行平滑，能不能对 Curvature 进行一个后期的平滑？不可以。因为 XY 坐标本身与 Curvature 是有联系的，不能单独平滑曲率，也不能单独平滑 X 或者 Y，今天的课程将为大家介绍平滑的方法。

多项式

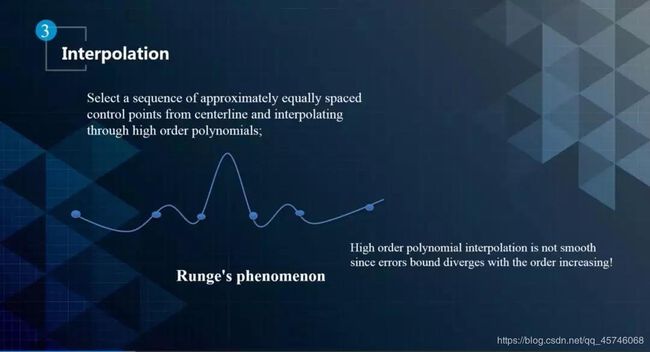
首先，可以在轨迹上以等距离的方式随机选择一些点，然后用高阶多项插值的方式来近似表示轨迹，对多项式进行优化。但是高阶多项式不能用于平滑，因为高阶的多项式抖动太大，没有办法控制幅度，这就是常说的龙格现象，如下图所示。

Bezier Spline

Bezier Spline 曲线是由一系列控制点定义的，例如 到 ，其中 n 代表曲线的阶数。如下图所示，分别给出 1 阶、2 阶、3 阶 Bezier Spline 曲线的表示形式。通过对它们做平滑，得到平滑的曲线，例如二阶平滑保证曲线的曲率平滑。但是这种方法的缺点是，除了起始点和终点，其它控制点不能保证会被得到的曲线经过。

生成一条光滑的曲线，涉及到两方面，一方面是目标，另一方面是工具。怎么定义平滑呢？最简单的方法就是最短路径，但是路径最短还不能保证平滑性，因此会对其不同阶导数进行 Minimize 求解，保证导数空间的连续，这就是 Smoothing Spline 最初的思想。那么，问题的目标就明确了，定义一个函数，能够最小化它的类似三阶导平滑性。

Smoothing Spline 具有一些特殊的性质，在给定边界的条件下，它是一个多项式，可以找到最优解。但是它的 Boundary Constraint 只考虑了起点和终点，如果中间有障碍物就不是最优解。这种情况下可以使用 Piecewise Polynomial（分段多项式）来处理。

Spline 2D

一个 Piecewise Polynomial 是一维的函数，描述二维曲线是不够的，这时候就有一个 Spline 2D，假设我们把曲线分成 N 截，每节曲线段它的 X 坐标是一个 Polynomial ，Y 坐标也是一个 Polynomial 。如下图所示，用 5 阶多项式来表示 X 和Y，称之为 Quintic Spline（五次样条），每一节都是这样的函数。这种表示有一个很好的特性，就是目标函数具有旋转不变性。怎么让曲线足够平滑？我们让它在 X 坐标上的变化率，也就是三阶导的平方是最小的，Y 上的变化率三阶导也是最小的，代价函数就是这两个变化率的和。代价函数的求解就是一个二次规划问题，我把这种 Loss Function 定义成这种形式是因为平方的积分能够给计算带来便利。

前面说的是用一节一节的线段来保证曲线是光滑的，在线段内部用一个二维的 Polynomial 表示，在内部是 N 阶可导的，但是如何保证节点处是平滑的呢？这个叫做端点约束条件，需要保证 X 和 Y 方向的倒数是相等的，一般要求到三阶导都是相等的，包括它的 X，Y 点的值也完全相等，此时就能保证三阶导连续。

Spiral Path

还有一种方式叫做螺旋曲线，它通过一个极坐标形式定义，比如说沿着一条曲线，如果一个点 S 的曲率是知道的，假设它的原点在 （0，0）的位置，可以唯一定义出一条经过 S 的曲线，也就是 Spiral Path 。那么可以让 Spiral Path 满足起点、终点约束条件生成一条螺旋曲线。

Spline 2D 与Spiral Path的区别

Spiral Path 和 Spline 2D 有什么区别呢？任何的曲线在足够密的时候都可以用Piecewise Spiral path 或者是 Piecewise Polynomial 表示。但是它们的出发点不一样，Polynomial 计算很快很简单，Spline 2D 是一个凸空间里面生成一个 Spline 曲线。Spiral Path 是从 Configuration Space 出发。理论上来讲，螺旋曲线生成的线是要比 Spline 更好处理，对一些极端情况处理更好。

五、optimization inside motion planning

约束问题的核心有三点：第一是目标函数的定义，目标函数比较清晰，对于后面的求解更有帮助。第二是约束，比如路网约束、交规、动态约束等。第三是约束问题的优化，比如动态规划、二次规划等。本节主要介绍动态规划和二次规划的基本概念，以及二次规划问题的求解方法和形式化方法。

动态规划

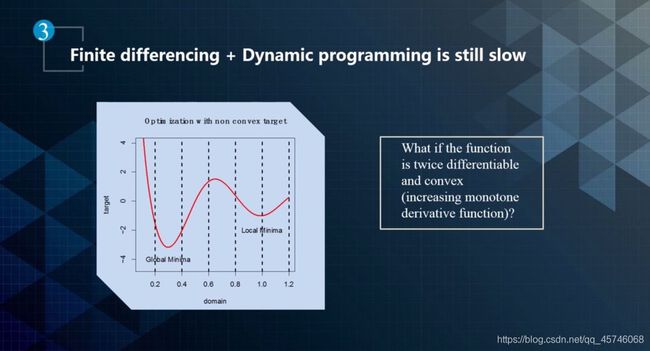
动态规划通过类似于有限元的方式，把问题从连续空间抽象成离散空间，然后在离散空间中进行优化。虽然这种方法可以逼近连续空间中的最优解，但是计算复杂度很高。针对计算时间长的问题，可以使用牛顿方法进行优化，它的收敛次数是指数平方，也叫二次收敛。

二次规划

二次规划算法的本质是牛顿法的 Taylor 展开，但是它的求解过程涉及更复杂的情况。因为二次规划方法并不一定是处理一维问题，可能涉及更高阶求导。在实践中，二阶导数基本可以满足问题需求。

二次规划问题的求解方法

首先通过动态规划方式对整个问题有一个粗浅的认识，然后通过二次规划进行细化。这种启发式搜索方法也是目前百度 Apollo 的 EM 算法的核心思想。这种方法和人开车的过程是一样的，通常驾驶员会先形成一个大概的指导思想，指明往什么方向开，然后再规划一条最优路径。

决策问题是一个离散空间中的优化问题，它的决定是什么？可以通过动态规划对整个空间先形成一个粗浅的认识，然后以此为启发，用二次规划求最优解。

一般来说，二次规划问题会写成一个二次函数，如下图所示。

其中，X 是向量参数，Q 是一个对称的正定矩阵， 是偏差项。对于这种没有约束的二次规划问题，只需要求导数等于0的那个点，使得 Qx=-C ，即可求解二次规划问题。这是一个线性方程组，它的求解速度是 O（N3）。

对于带约束的二次规划问题，情况就相对复杂一点，如下图所示。

这种情况可以有很多种解法，其中一种把限制条件放到上面的式子中，通过换元，变成一个全新的 QP 问题求解，但是这种方法很慢。另一种方法是 Lagrangian method ，通过增加松弛变量的方式去掉约束条件，变成一个可以解决的问题。

对于不等式的约束条件，如何去求解呢？可以使用 active set method，其主要出发点是最后解，可能落到边界上，如果真的是边界最优，不等式约束就可以转化为等式约束问题求解。有人总结出求解二次规划问题的方法 KKT，其主要思想如下图所示。

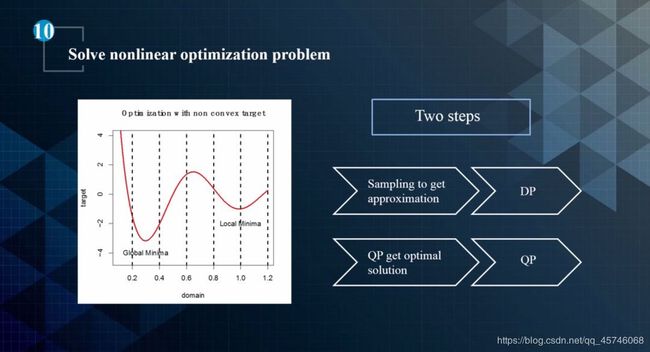
总的来说，对于求解非线性优化问题（自动驾驶中的规划基本都是非线性的），通常就是用启发式方法来求解。先用动态规划给出一个粗略解，给出一个凸空间。然后用二次规划方法在凸空间里去寻找最优解，如下图所示。

六、understand more on the MP difficulty

本节主要介绍 Apollo 中的 EM planner 。在前面的课程中，我们提到优化问题的三个方面：目标函数、约束条件和求解方法。那么在实际过程中无人车怎样去抽象约束呢？先看一个简单的例子，如下图所示。

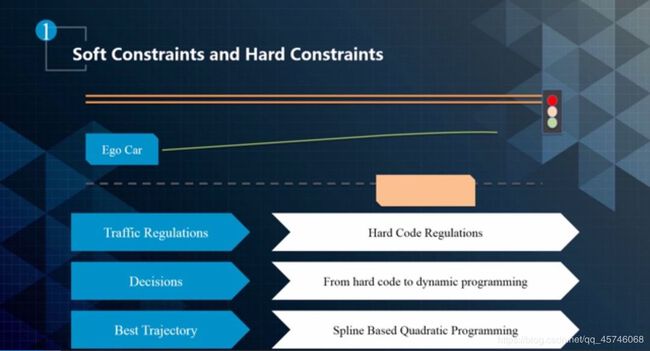
在这个场景中，有三类约束，第一个叫做 Rraffic Regulation，第二个是 Decisions，第三个是 Best Trajectory 。这些限制又分为硬限制和软限制，例如交通规则属于硬性限制。

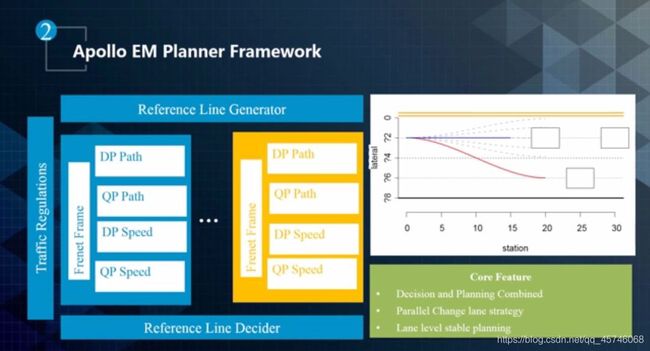
Apollo EM 规划框架

在 Apollo 中，我们设计了一个 EM 规划框架来处理不同的场景，如下图所示，展示处理一个换道场景。在蓝线和红线交点处发现前方有车辆行驶缓慢，可能要进行换道处理。如果只是简单的看到旁边没有车就换道，可能会导致危险发生。在 Apollo EM 规划框架中，我们会对换道和继续在本车道行驶分别规划出一条轨迹，只有换道之后的 Trajectory 要比本车道的 Trajectory 好的情况下才换道。在 Apollo 的 EM planner中，决定哪个道比较好的模块叫做 Reference Line Decider，中间的并行模块是通过 Path Speed Iterative 的方式并行实现的。

优化决策问题

优化决策问题本身是一个 3D optimization 问题，其中包含了三个维度，需要生成 SLT 。三维空间的优化相对比较复杂，常用的方法有两种：一种就是离散化的方式去处理。另一种方法是 Expectation Maximization（期望最大化）。其基本思想是降维处理，先在一个维度上进行优化，然后在优化的基础上再对其它维度进行优化，并持续迭代以获得局部最优解。

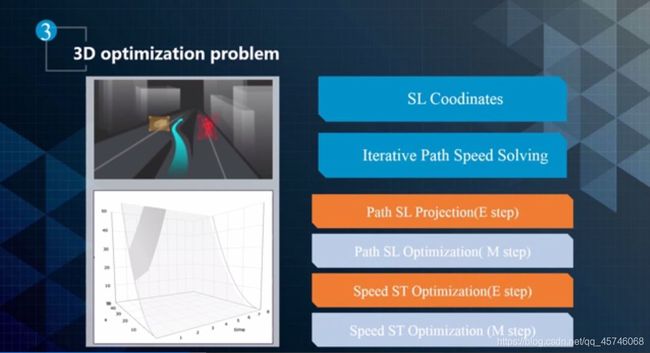
对于无人车，Apollo 上的 EM planner 对 Path-Speed 进行迭代优化。首先，生成一条 Optimal Path ，在最优路径的基础上生成 Optimal Speed Profile 。在下一个迭代周期，在优化后的 Speed 的基础上，进一步优化 Path，依次类推。它分了四步走，其中分为两步 E step 和 M step 。这种算法的缺点是不一定能收敛到全局最优解。

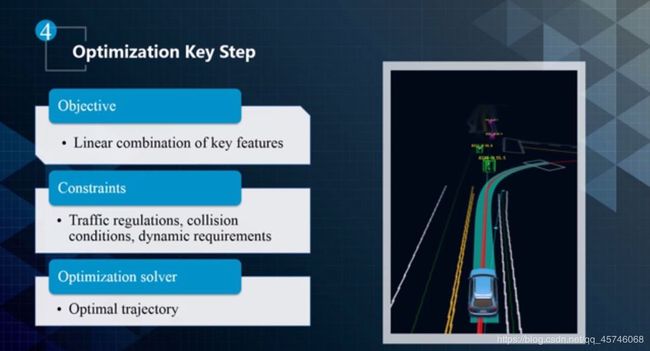
优化问题的关键步骤包括： Objective Functional、Constraint、Solver。目标函数是一些关键特征的线性组合。约束主要包括交通灯、碰撞以及动态需求等。优化求解方法的目的是找到最佳路径，包括前面讲的动态规划+二次规划的启发式方法。

非线性优化问题

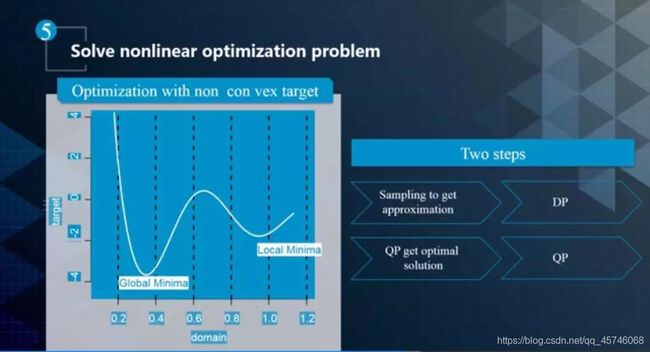
对于非线性优化问题，通常都是分两步走，一是动态规划，先找一个粗略解。然后再是二次规划，从粗略解出发，找出一个最优解。以路径规划为例，假设前方有一个障碍物，首先做出从左边还是右边的避让决策，然后通过 QP 生成一条平滑的曲线去避让障碍物。对于速度而言，先通过动态规划的方式给出一个粗略的解，然后再通过二次规划的方式给出一个更平滑的解。

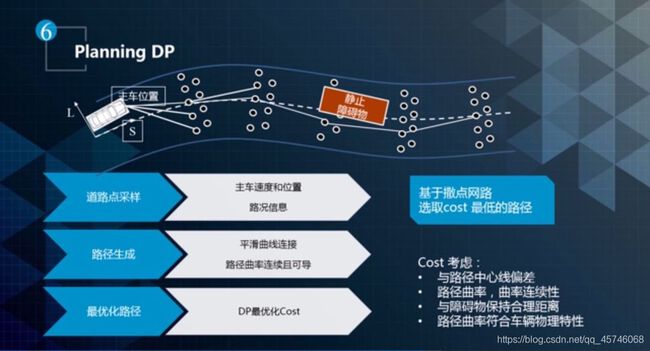
具体来讲，在决策规划里如何动态规划 Path 呢？先确定主车的位置，然后往前排撒若干点，基于撒点网络得到一个代价最低的路径，这时候的路径不够平滑。

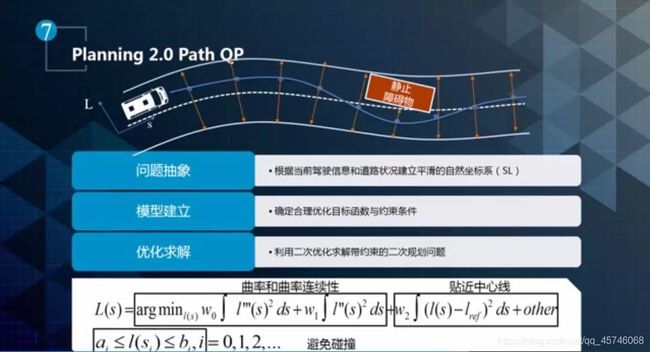
我们可以利用二次规划方法，生成一条平滑的轨迹如下所示：

然后利用二次规划方法，按照问题抽象、模型建立和优化求解的步骤生成一条平滑的轨迹。

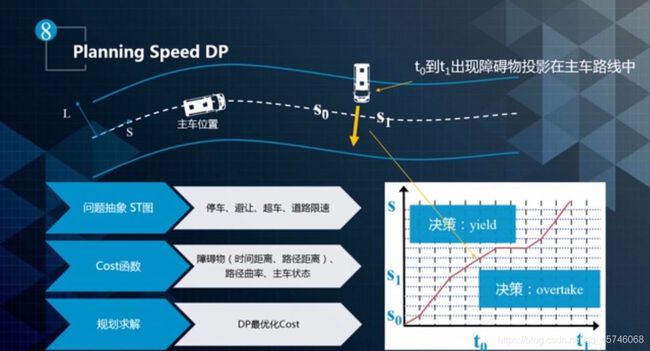
对于速度的优化，同样是类似的，如下图所示。

规划问题如何解决逆行

对于逆行的处理，首先根据当前 Speed Profile 去估计当前逆行障碍物的位置，然后再修正 Path，根据修正之后的 Path 再来处理 Speed，例如需要减速。减速之后，估计需要重新改变路径，依此类推，直到得到理想的规划轨迹。

目前，百度 Apollo 无人车项目的规划模块进展如下图所示，支持在城市和高速等环境下的多种驾驶场景处理，包括直行、转向、路口、停车等。

七、reinforcement learning and data driven approaches

强化学习和数据驱动方法

决策问题通常用 POMDP 加上一些机器学习的技术来解决。在前面我们已经介绍过，解决好规划问题，需要把两个方面做好，一个是数据闭环（Data Driven），另一个是基于规则的方法。数据驱动是在基于规则的闭环里面的小闭环。Rule Based 的方法可以对遇到的新案例，很快给出解决方案。

在基于规则的方法的基础上，对问题形成一定的认识，通过把问题抽象成更加通用的问题，定义目标函数来进一步优化问题。数据驱动的方法就是通过大量的案例统计分析，得到模型，使得遇到类似问题的时候，不需要过多的考虑，直接套用数据驱动的模型获得结果， Data Driven 的方法其实就是基于经验的方法，只不过这些经验是模型通过大量的样本数据学习得到的。

本次学习有点多，能坚持看完的你，一定是个很厉害（牛逼）的人，希望你还对无人驾驶充满兴趣。