信号的反射(振铃、台阶、回勾、尖峰毛刺)
1. 反射是怎么形成的
假设信号传输过程中,经过两个阻抗不同的区域,如下图所示。区域1阻抗为Z1,区域2阻抗为Z2。
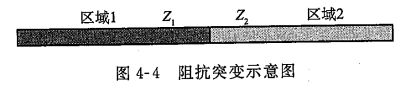
在分界面处,电压必须是连续的,否则,在分界面处会产生无穷大的电场,这在真实世界中是不可能的。
同样,分界面两侧的电流必须是连续的,否则分界面处会产生无穷大的磁场。
因此:
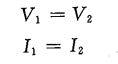
根据欧姆定律,必然有:
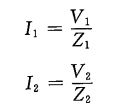
显然如果Z1≠Z2的情况下,上面式子不可能同时成立。如何理解这一困境?
应该从电磁波的角度来理解反射,在分界面处,一部分正向传播,另一部分反向传播。
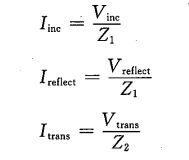
从电压电流角度,我们可以把区域1的电压V1分成两部分,其中一部分以电压Vinc正向传输,另一部分以电压Vreflect反向传输。其中Vinc称为入射电压,Vreflect称为反射电压,而V2记为Vtrans,称作传输电压。由于分界面两侧电压相等,所以有:
V i n c V_{inc} Vinc + V r e f l e c t V_{reflect} Vreflect = V t r a n s V_{trans} Vtrans
再看电流情况。入射电压Vinc 产生一个正向电流Iinc,反射电压Vreflect 产生一个反向电流Ireflect。区域2的电流记为Itrans,要使分界面两侧电流相等,必有:
I i n c I_{inc} Iinc- I r e f l e c t I_{reflect} Ireflect= I t r a n s I_{trans} Itrans
再根据欧姆定律:
联立上面五个式子,可得
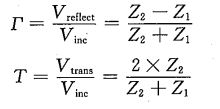
第一个计算的是反射系数
第二个计算的是传输系数
有两种特殊情况的反射,那就是末端开路和末端短路。
末端开路情况:
相当于Z2= ∞ ,根据上式计算反射系数为1,所有入射电压全部被反射,而且幅度与入射电压相同,且极性相同。这是末端电压式入射电压的2倍。
下图是末端开路情况下仿真结果:
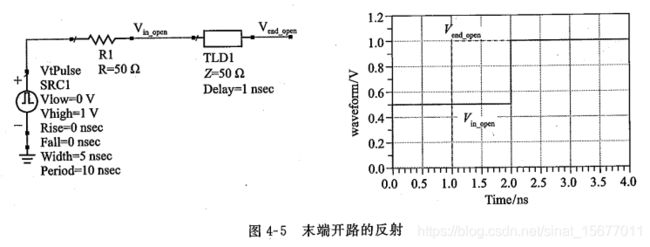
信号在0ns时刻从0跳变到1V,信号源输出阻抗为50Ω,传输线特性阻抗也为50Ω,根据分压关系施加到传输线上的电压 V i n o p e n V_{in_open} Vinopen幅度为0.5V。传输线延时为1ns,在小于1ns的时间段内0.5V的信号尚未到达传输线末端,传输线末端电压 V e n d o p e n V_{end_open} Vendopen保持为0V。在1ns时刻,信号刚好传输到末端,如过不发生反射的话,末端电压 V e n d o p e n V_{end_open} Vendopen应该是0.5V,但实际上看到是1V。产生这种现象的原因就是入射的0.5V信号发生反射,反射电压也是0.5V(反射系数为1 ), V e n d o p e n V_{end_open} Vendopen是入射电压和反射电压的叠加,刚好是1V。再看传输线入口处的信号波形,2ns时 V i n o p e n V_{in_open} Vinopen
从0.5V跳变为1V,注意传输线延时为1ns,末端反射的0.5V信号传播到发送端的时刻刚好是2ns。反射回路的0.5V电压和入射的0.5V电压叠加(此时输入电压仍然在),电压跳变为1V。
末端短路情况:
这时,Z2=0,根据公式计算反射系数为-1,反射幅度与入射电压相等,但极性相反,叠加的结果是末端电压为0,这与短路的情况相符合。
下图为末端短路情况的仿真结果:
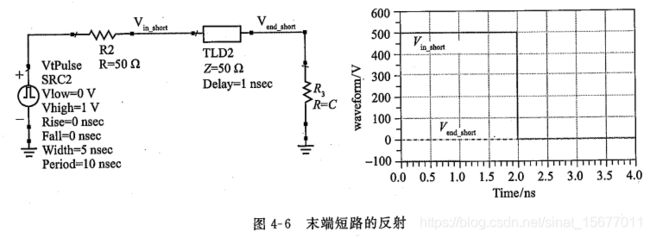
与开路情况分析类似,0.5V信号在1ns时刻传播到末端,反射系数为-1,反射电压为-0.5V,反射电压和入射电压叠加结果为0V。2ns时刻,反射回来的-0.5V电压和入射到传输线上的电压相叠加,结果为0V。
2. 计算反射波形(振铃)
使用特性阻抗为50Ω的传输线,信号上升时间0ns,即理想方波信号,传输线延时为1ns,传输线末端开路,并且假定驱动器输出阻抗为10Ω,其反射图如下图所示:
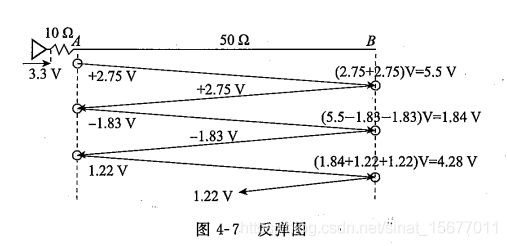
第一次反射:
信号在0ns时从芯片内部发出,经过10Ω输出阻抗和50Ω PCB特性阻抗的分压,实际加到PCB走线上的信号为A点电压
[3.3x 50/(10+50)]V=2.75V。1ns后信号传输到远端B点,由于B点开路,阻抗无穷大,反射系数为1,反射信号电压为2.75Vx1=2.75V。此时B点测量电压是(2.75+2.75)V=5.5V。这里需要注意的是,在t=1ns这一时刻,B 点的测量电压是入射电压与反射电压的叠加。
第二次反射:
2.75V的反射电压在t=2ns时刻回到A点,阻抗从50Ω变为10Ω,发生负反射,此时从B点反射回来的2.75V信号向A点传播,对于A点来说相当于入射电压,反射系数为 :
(10-50)/(10+50)= - 2/3
所以A点反射电压为2.75Vx(-2/3)=-1.83V。此时A点测量电压同样是原本电压、入射电压和反射电压的叠加,即
(2.75+2.75-1.83)V=3.67V
第三次反射:
-1.83V反射电压向B点传输,t=3ns时刻到达B点,再次发生全反射,反射电压也是-1.83V。此时B点测量电压为(5.5-1.83-1.83)V=1.84V(原本电压、入射电压和反射电压的叠加)
第四次反射:
从B点反射回的-1.83V电压在4ns时到达A点,再次发生负反射,反射电压为1.22V。此时A点测量电压为(3.67-1.83+1.22)V=3.06V。
第五次反射:
1.22V反射电压在5ns时到达B点再次发生反射,反射电压也是1.22V。此时B点测量电压为(1.84+1.22+1.22)V=4.28V。
后面的反射同理计算。。。。
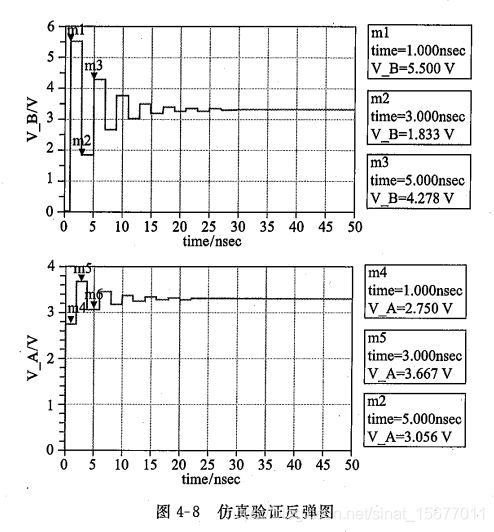
观察B点电压:5.5V->1.84V->4.28V->。。。可见B点电压会有上下波动,这就是信号振铃。
观察A点电压:2.75V->0.92V->2.14V->。。。也同样存在振铃现象。
A/B点仿真波形如下图:
假设A点的反射系数都表示为 Γ \Gamma ΓA; B 点反射系数表示为 Γ \Gamma ΓB。
入射电压表示为Vin=2.75V , 各次反射电压可以表示如下:
第一次反射电压:Vin Γ \Gamma ΓB=2.75V
第二次反射电压:Vin Γ \Gamma ΓB Γ \Gamma ΓA=-1.83V
第三次反射电压:Vin Γ \Gamma ΓB Γ \Gamma ΓA Γ \Gamma ΓB=-1.83V
第四次反射电压:Vin Γ \Gamma ΓB Γ \Gamma ΓA Γ \Gamma ΓB Γ \Gamma ΓA=1.22V
可以想象,随着反射次数的增加, Γ \Gamma ΓB和 Γ \Gamma ΓA的累计相乘越来越多,由于A点的反射系数的绝对值小于1,所以这个累计相乘的结果会越来越小,反射电压的绝对值也会越来越小,其极限值为0。对于无损传输线,信号会在AB两点之间无休止地振荡下去,但现实中地传输线都是有损地,信号反复传播振荡过程会不断衰耗,最终趋于稳态值。
3. 容性阻抗不连续
对于电阻性阻抗不连续,在阻抗不连续点两侧的阻抗值都是固定的,因而反射系数是恒定的数值。但是对于容性不连续点,信号感受到的阻抗却是随时间变化的,因而反射系数也是变化的。在下图RC电路中,激励源从低电平跳变到高电平,假设高电平电压幅值为A,则电容两端的电压可表示为:Vc=A(1- e t / τ e^{t/\tau} et/τ)
其中, τ \tau τ =RC为电路的时间常数。电容从充电开始,经过一个时间常数 τ \tau τ后的电压值为:
![]()
即,经过一个时间常数后电容电压值上升到其终值电压的63.2%。
流过电容的电流为:
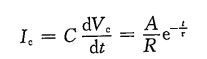
因此,电容的阻抗可表示为:
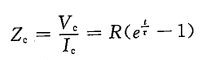
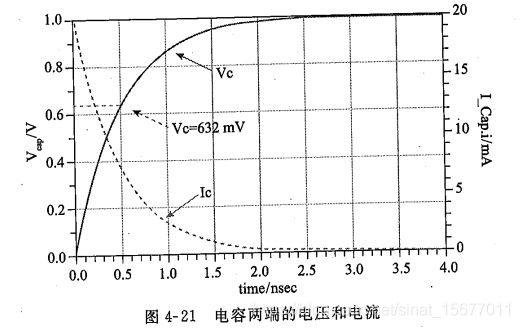
如果R=50Ω,C=10pF,当激励源是上升时间为0的阶跃信号时,电容两端的电压和电流变化曲线如下图所示:
开始时刻,有很大的充电电流,电容两端电压迅速上升,随着电容充电,电压上升速度减缓,充电电流也逐渐减小。
当t= τ \tau τ=500ps时,电容电压上升到632mV,是终值电压1V的63.2%。
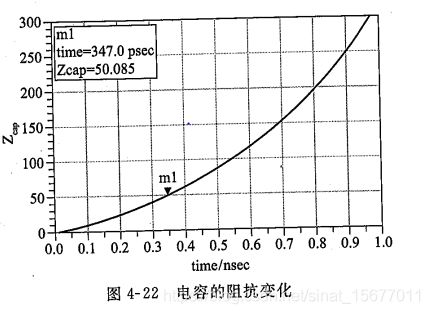
电容阻抗变化如下图所示,电压刚刚施加到电容上的瞬间,电容的阻抗为0,相当于短路。随着电容充电,阻抗逐渐增大。随着时间的不断增加,阻抗逐渐变为无穷大,最终相当于开路。
当t= τ \tau τ*In2时,电容阻抗等于R。RC电路时间常数 τ \tau τ=RC越大,电容阻抗变化越缓慢;反之,越快。
4.互连线末端容性负载的反射(回勾)
任何接收器都会有一定的输入电容,焊盘、封装都会引入一定的寄生电容,硅片也存在寄生电容。输入电容可能从几皮法到十几皮法不等,通常是几皮法。
这个输入电容对于信号来说就是一个容性阻抗不连续点,当信号到达接收器时,就会因为容性不连续而产生反射。
如下图所示,信号进入传输线但尚未到达末端这段时间内,它并不清楚末端是什么,信号感受到的就像一个纯电阻电路,阻抗为传输线特性阻抗Z0。信号抵达传输线末端时刻,感觉到一个容性的负载,对信号而言,就是从一个阻性元件进入容性元件,因而时间常数可表示为:
τ \tau τ=Z0 C
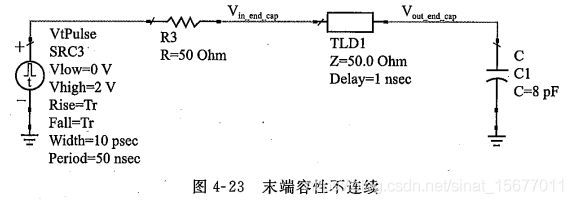
假设激励信号上升时间Tr=0,输出阻抗为50Ω,传输线阻抗为Z0=50Ω,传输线延迟时间为1ns,末端电容C=8pF。传输线入射的波形上升时间为0,幅度为1V的理想方波(信号还没到达末端,2产生分压)。当这个方波信号经过1ns的传输延迟后到达末端电容负载的瞬间,电容会有一个很大的充电电流,随着电容的充电,电压逐渐增大,电流逐渐减少。
电容的阻抗为:
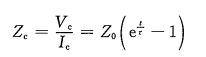
电流电压阻抗变化曲线:
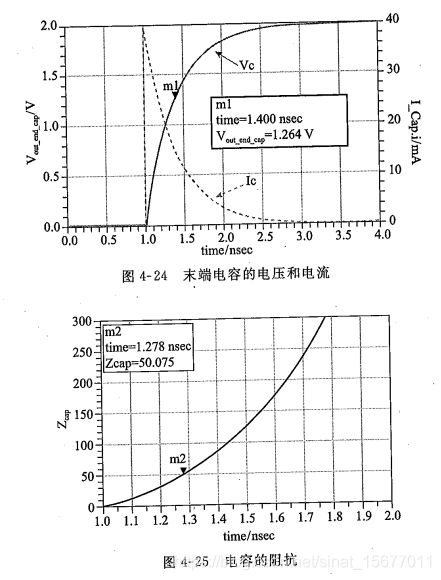
对于容性负载来说,由于阻抗是时变的,所以导致反射系数也是时变的。
反射系数可表示为:
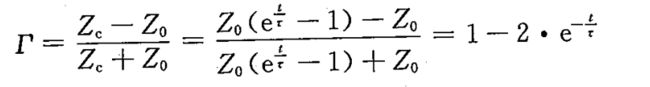
其中 τ \tau τ=Z0 C。
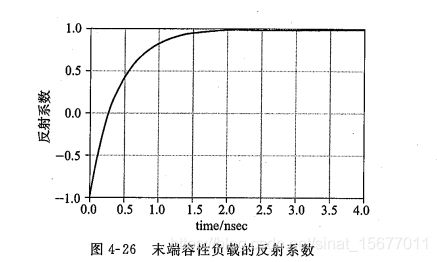
当信号入射到电容的瞬间,即t=0时刻,电容开始充电,此时电容阻抗为0,反射系数为-1,相当于短路情况。
当t= τ \tau τ*ln2时,电容阻抗等于传输线阻抗,此时反射系数为0。
当t->∞时,电容的阻抗远大于传输线的阻抗,反射系数为1,相当于开路情况。
容性负载使电路工作状态经历从短路到开路的转化。反射系数随时间变化趋势下图:
产生一个与信号跳变方向相反的脉冲波形。如果在传输线的发送端附近还有其他的接收器,那么这个向下的尖峰就会非常危险。
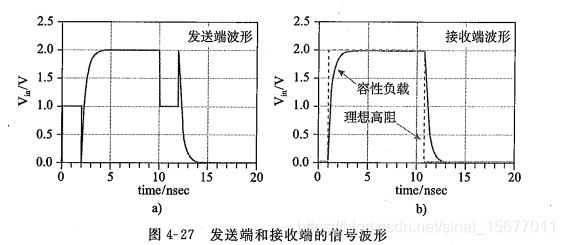
上图解析:
2V激励源入射到传输线后,产生分压,传输线入射信号为1V(输出阻抗与传输线阻抗都是50Ω),经过1ns延迟后抵达接收端,由于容性负载刚开始充电时刻相当于短路状态,反射系数为-1,产生-1V反射信号传回发送端,此时接收端信号为入射信号+反射信号=1V-1V=0V;再经过1ns延迟后反射信号传回发送端,刚好与发送端相抵消,发送端电压被拉低到0V。
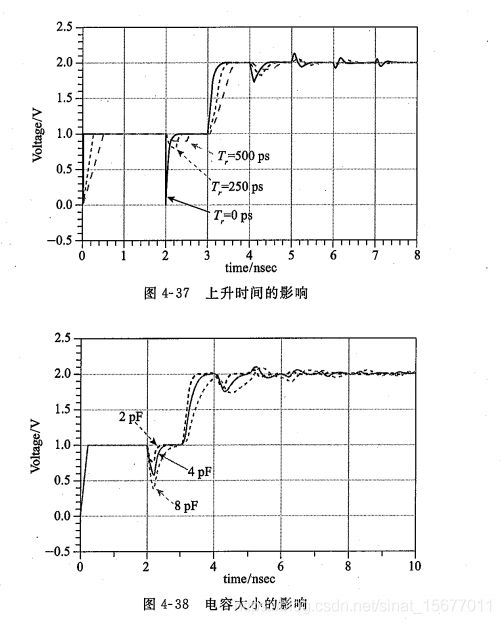
实际的数字信号上升时间不是0,这时发送端波形如下图:
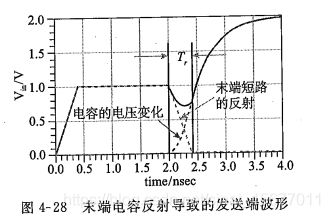
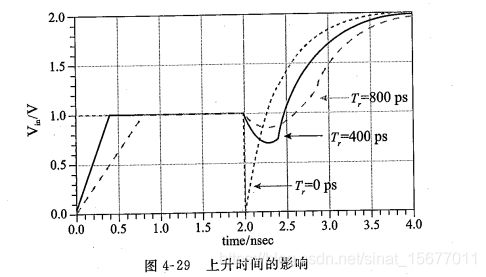
回勾的深度和信号上升时间有关:
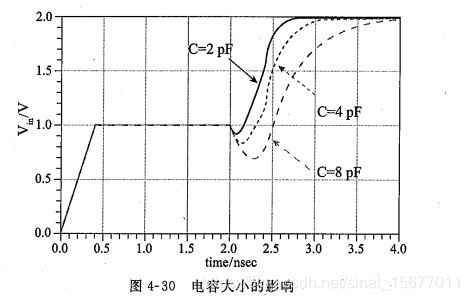
末端电容的反射噪声对电容值和信号上升时间很敏感,增加信号上升时间能显著减少容性负载的反射噪声。
互连线中间容性负载的反射
容性负载不仅仅表现为接收器的输入电容,而且还表现在类似于容性结构的负载,如芯片引脚较宽的焊盘也类似于一个容性负载,对于低速信号,过孔也可以粗略地看作是一个容性负载。如果PCB走线经过过孔换层,就类似在传输线中间有一个小地容性负载。如下图:

接收端和发送端仿真波形如下,
在发送端,2ns后容性负载的反射信号回到发送端,反射信号和入射信号叠加的结果是波形电压降到0V,此后,信号电压按照指数的规律增加,上升时间由时间常数决定(Z0C /2)。注意高电平上叠加很多噪声,这是由于末端负载和电容之间发送多次反射,因此信号在两点之间反复震荡;信号每一次传输到电容所在的位置时,都会有一部分信号在发送端叠加在高电平上从而形成噪声。
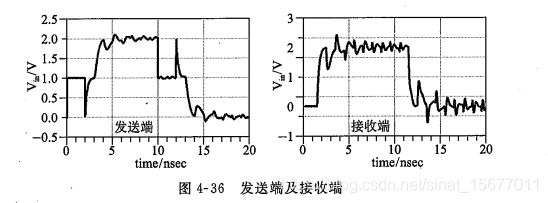
对于接收端,容性不连续发生两种作用:
1)信号的上升沿由于电容的作用变缓
2)高电平和低电平都会叠加一定的噪声。信号到达接收端后,由于接收端的高阻抗而发生反射,反射信号幅度等于入射信号幅度。反射回来的信号到达中间电容时再次发生反射,反射电压为负值,这个信号传播到接收端并叠加在接收端信号上,产生了波形中的第一个回勾。沿着信号传播路径继续走,这个负的信号在接收端再次发生反射,幅度翻倍,再次传播到电容处,在电容处发生负反射变为一个正的信号向接收端传播,在接收端波形上形成一个过冲。
5. 感性阻抗不连续
封装引脚、板间连接器等都表现为典型的感性不连续。对于感性不连续点,信号感受到的阻抗是随时间变化的,因而反射系数也是变化的,如下图RL电路:
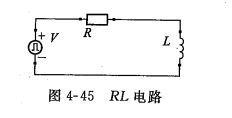
假设高电平电压为A,则流过电感的电流为:
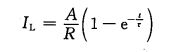
其中, τ \tau τ=L/R
电感两端的电压可表示为:
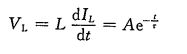
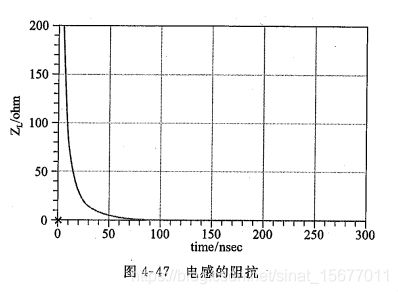
因此,电感阻抗可表示为:
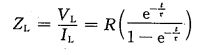
如果R=50Ω,L=1nH,当激励源上升时间为0的阶跃信号时,电感两端的电压和电流变化曲线如下图:
由于电感的电流不能突变,开始时刻电流为0,电感相当于开路,因此此时电感的电压和激励源电压相等.随着电感电流逐渐增加,而电感两端电压快速下降.
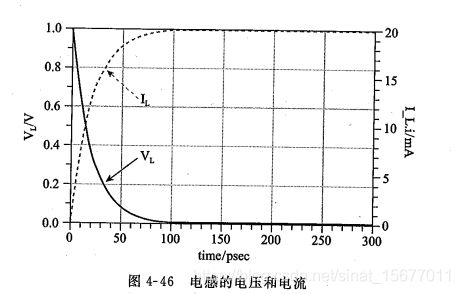
电感的阻抗如下图,电压刚刚施加到电感上的瞬间,电感的阻抗为无穷大,相当于开路.接着电感阻抗迅速减小.随着时间的推移,阻抗逐渐趋向于0,最终相当于短路,电感的阻抗具有时变的特性.
6.互连线末端感性负载的反射(尖峰毛刺)
如下图,感性负载在互连线的末端。
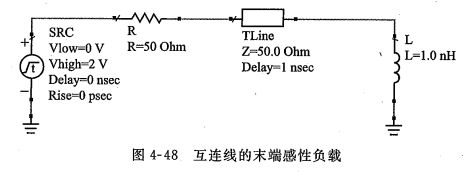
信号进入传输线但尚未达到末端这段时间内,它并不清楚末端连接的是什么,信号感受到的就像一个纯电阻电路,阻抗为传输线特性阻抗Z0。信号抵达传输线末端时,感受到一个感性的负载,对信号而言,就是从一个纯阻性元件进入感性元件,其时间常数表示为
![]()
由于感性负载的阻抗是时变的,因而信号的反射系数也必然是时变的,由反射系数计算得感性负载的反射系数为:
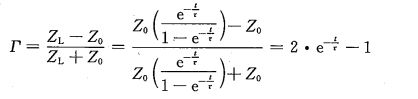
下图显示感性负载反射系数的变化趋势,在信号入射的瞬间,反射系数为+1。
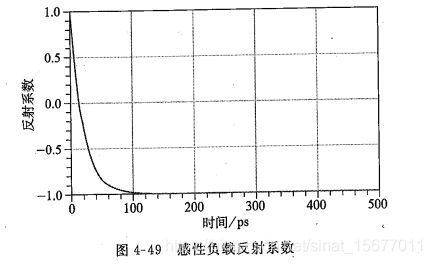
传输线发送端和接收端的波形如下:
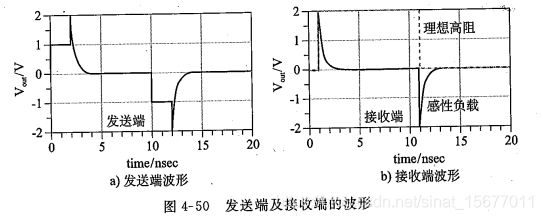
发送端:
由于传输线延迟1ns, 1ns时刻1V入射信号传输到末端遇到感性负载时,此时的感性负载相当于开路状态,反射系数为1,所以反射信号也为1V,经过2ns后反射信号传回发送端和入射信号叠加的结果使波形电压冲到了2V,此后,信号电压按照指数规律下降,下降时间由时间常数L/Z0决定。经过一定时间后信号电平变为0(此时感性负载相当于短路)。在入射信号的下降沿,变化规律类似。
接收端:
如果接收端是一个高阻的阻性不连续,比如开路状态,那么接收端波形将会是图中虚线所示波形。但感性负载使接收端信号的电平迅速下降,最终波形类似于一系列的尖峰脉冲,像噪声一样,失去了方波特征。
如果上升时间Tr≠0,反射波形如下图所示,
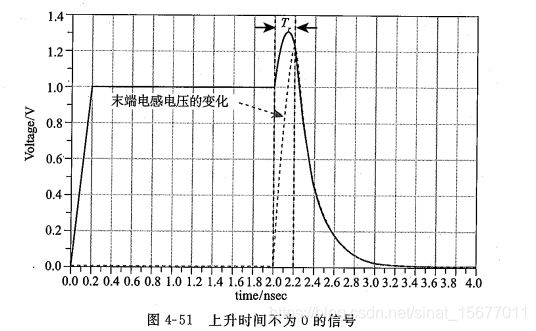
t=2ns时刻,反射信号到达发送端,在信号上升时间Tr间隔内,发送端波形是入射波形和电感反射波形叠加。
解析:
比如刚开始(0ns~0.2ns时间段)发送端发生上升沿信号到末端,经过1ns延迟后,到达感性负载末端,末端反射系数刚开始是接近1(全反射),但随着上升沿信号到达电感,电感电流在渐变,阻抗也在改变,此时反射也在减小(比1小),所以对上升沿的反射波形类似发送端上升沿,但并不像理想方波一样全反射(入射1V也反射1V),而是要小些。
反射信号在2ns时刻反射信号刚好传回发送端,与发送端入射信号相叠加,就出现突起的波形(比如1V+反射上升沿波形)。发送端波形不会上冲到入射电压两倍。
在反射信号到达发送端,并经过一个Tr时间间隔后,发送端波形和电感两端电压波形变化趋势一致。
上冲幅度和信号上升时间有关。上升时间越长,反射噪声就越小。较长的上升时间可以容忍更大的感性不连续。
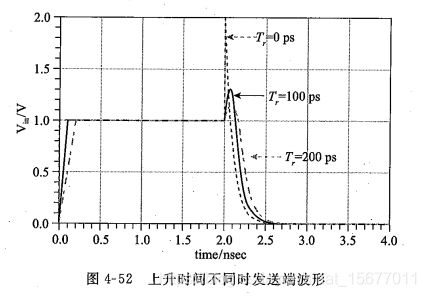
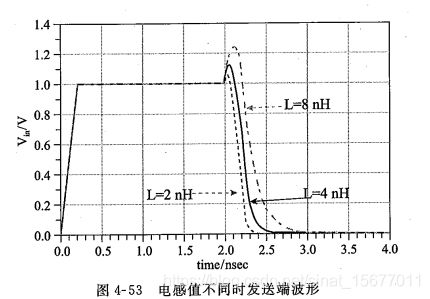
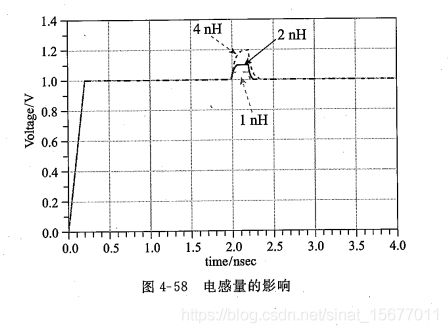
上冲的幅度还和感性负载的大小有关。感性负载越大,反射噪声也越大。
7. 互连线中间感性负载的反射
经常遇到感性负载在链路中间的情况,比如信号经过连接器从一块板传输到另一块板,连接器称性出典型的感性负载特征。
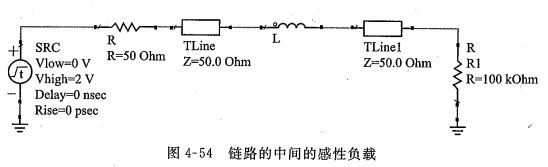
如果上升时间Tr=0,传输线发送端和接收端的波形如下:
在发送端,信号到达感性负载的瞬间,电感阻抗无穷大,发送全反射,2ns后感性负载的反射信号回到发送端,信号波形上升到2V。此后,信号电压按照指数规律下降,下降时间由时间常数决定。在下降沿,产生一个与信号跳变反向相同的脉冲波形。注意高电平和低电平上都叠加有很多噪声,这是由于末端负载和电感之间发送多次反射,信号在两点之间反复震荡,每一次传输到电感位置时,都会有一部分信号返回发送端叠加在高电平上形成噪声。
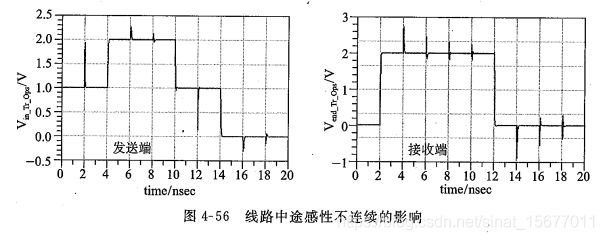
信号到达接收端后,由于接收端的高阻抗而发生反射,反射信号幅度等于入射信号幅度。反射回来的信号到达中间的电感时再次发生反射,反射电压为正值(电感阻抗大),这个信号传播到接收端并叠加在接收端信号上,产生了波形中的毛刺。
尖峰毛刺的幅度和上升时间有关,上升时间越长,反射噪声就越小。
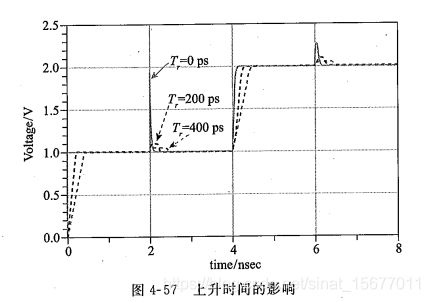
尖峰毛刺的幅度还和感性负载的电感量大小有关。感性负载越大,反射噪声也越大。
整理自《信号完整性揭秘》